Тема 2.1. Случайные величины и случайные вектора
Тема 2.2. Числовые характеристики распределений случайных величин
Тема 2.3. Основные законы распределений случайных величин
Рекомендуемая литература
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие/ В. Е. Гмурман. – М.: Высшее образование, 2010.
2. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие/ В. Е. Гмурман. – М.: Высшее образование, 2010.
3. Теория вероятностей и математическая статистика: учеб. пособие [Электронный ресурс] /В.С. Мхитарян [и др.].— М.: Московский финансово-промышленный университет «Синергия», 2013.— 336 c.— Режим доступа: https://www.iprbookshop.ru/17047
Задачи по теории вероятностей.
Рекомендации по выполнению заданий 1-9
1. Теоретический материал и подробное решение типовых задач по теме: «Классическое вероятностное пространство» можно найти в § 3, § 5 главы I учебника [1]; в § 1 главы I учебного пособия [2]
2. Теоретический материал и подробное решение типовых задач по теме: «Теоремысложения и умножения» можно найти в главах II и III учебника [1] (стр. 31-44), в § 1, § 2 главы II учебного пособия [2].
3. Теоретический материал и подробное решение типовых задач по теме: «Формула полной вероятности и формулы Байеса» можно найти в § 2, § 3 главы IV учебника [1] (стр. 50-54); в § 3, § 4 главы II учебного пособия [2].
4. Теоретический материал и подробное решение типовых задач по теме: «Повторение испытаний» можно найти в § 1 главы V учебника [1] (стр. 55); в § 1, § 4 главы III учебного пособия [2].
Решение задачи № 1
Событие 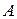 можно словесно описать так: нужная формула содержится в 1-м справочнике и не содержится во 2-м и 3-м, или формула содержится во 2-м справочнике и не содержится в 1-м и 3-м, или формула содержится в 3-м справочнике и не содержится в 1-м и 2-м. По определению произведения событий и противоположного события первая фраза соответствует событию
можно словесно описать так: нужная формула содержится в 1-м справочнике и не содержится во 2-м и 3-м, или формула содержится во 2-м справочнике и не содержится в 1-м и 3-м, или формула содержится в 3-м справочнике и не содержится в 1-м и 2-м. По определению произведения событий и противоположного события первая фраза соответствует событию  , вторая фраза – событию
, вторая фраза – событию  , третья фраза – событию
, третья фраза – событию 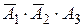 . Теперь из определения суммы событий получаем:
. Теперь из определения суммы событий получаем:
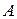 =
=  +
+  +
+ 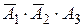 .
.
Событие  описывается так: нужной формулы нет ни в 1-м, ни во 2-м, ни в 3-м справочнике. Опять по определению произведения событий и противоположного события получаем:
описывается так: нужной формулы нет ни в 1-м, ни во 2-м, ни в 3-м справочнике. Опять по определению произведения событий и противоположного события получаем:
 =
=  .
.
Из определения противоположного события ясно, что  . Поэтому
. Поэтому
 =
=  .
.
Такой способ записи  полезен, если требуется вычислить вероятность этого события. Другой способ записи события
полезен, если требуется вычислить вероятность этого события. Другой способ записи события  вытекает из его словесного описания: нужная формула содержится или в 1-м справочнике, или во втором, или в третьем. То есть
вытекает из его словесного описания: нужная формула содержится или в 1-м справочнике, или во втором, или в третьем. То есть
 .
.
Совпадение двух полученных выражений следует из одного из законов Де Моргана (покажите это самостоятельно!).
Решение задачи № 2
Для решения этой задачи нужно хорошо освоить определение классического вероятностного пространства.
Результатом каждого бросания двух костей является пара чисел, выпадающих на верхних гранях этих костей. Таким образом, пространство элементарных событий (исходов), связанное с данным экспериментом, есть множество упорядоченных пар  , где
, где  и
и  принимают значения 1,2,…,6. Следовательно, множество элементарных событий
принимают значения 1,2,…,6. Следовательно, множество элементарных событий  состоит из 36 элементов. Так как выпадения любых двух таких пар можно считать равновероятными, то для расчета вероятностей следует применять классическую схему. Итак,
состоит из 36 элементов. Так как выпадения любых двух таких пар можно считать равновероятными, то для расчета вероятностей следует применять классическую схему. Итак,  .
.
а) Сумма выпавших очков равна 8 у следующих исходов:  ,
,  ,
,  ,
,  ,
,  ,
,  . Следовательно,
. Следовательно,  и
и 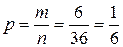 .
.
б) Сумма выпавших очков равна 6, а произведение 9 только у исхода  . Следовательно,
. Следовательно,  и
и  .
.
в) Сумма выпавших очков  у следующих исходов:
у следующих исходов:  ,
,  ,
,  ,
,  ,
, 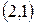 ,
,  ,
,  ,
,  ,
,  ,
,  . Следовательно,
. Следовательно,  и
и  .
.
г) В данном пункте разность очков понимается в том смысле, что из большего выпавшего числа вычитается меньшее. Таким образом, разность выпавших очков меньше 2 у следующих исходов:  ,
,  ,
, 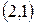 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 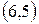 ,
,  . Следовательно,
. Следовательно,  и
и  .
.
д) Сумма очков расположена в промежутке [4; 10] (событие 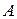 ) у следующих исходов:
) у следующих исходов:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 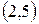 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 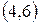 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Следовательно,
. Следовательно,  и
и  . Эту задачу можно решить проще, если перейти к противоположному событию
. Эту задачу можно решить проще, если перейти к противоположному событию  : сумма выпавших очков меньше 4 или больше 10. Этому событию благоприятствуют исходы:
: сумма выпавших очков меньше 4 или больше 10. Этому событию благоприятствуют исходы:  ,
,  ,
, 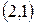 ,
,  ,
, 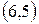 ,
,  . Следовательно,
. Следовательно,  ,
,  и
и  . Результаты в обоих решениях совпадают.
. Результаты в обоих решениях совпадают.
Решение задачи № 3
Эксперимент в данной задаче состоит в извлечении наудачу трех из шестнадцати деталей, находящихся в ящике. Будем считать две такие выборки из 16-ти деталей по 3 различными, если одна из этих выборок содержит деталь, не принадлежащую другой. Число различных выборок из 16-ти по 3 равно, как известно,  . Эти выборки естественно считать равновероятными, поэтому применима классическая схема. Таким образом,
. Эти выборки естественно считать равновероятными, поэтому применима классическая схема. Таким образом,  .
.
а) Событию «извлеченные детали качественные» благоприятствуют те выборки, которые получаются извлечением деталей только из 12 качественных деталей, находящихся в ящике, то есть  . Следовательно,
. Следовательно,
 .
.
б) Событию «среди извлеченных деталей 2 бракованные» благоприятствуют те выборки, которые получаются, когда одна деталь извлечена из группы двенадцати качественных деталей, а 2 детали извлечены из группы четырех бракованных деталей. В такой выборке одна качественная деталь может произвольным образом «состыковываться» с двумя бракованными деталями. Поэтому  . Следовательно,
. Следовательно,  .
.
Решение задачи № 5
Для решения данной задачи нам понадобится понятие условной вероятности.
Введем события:
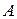 – при изготовлении формы возникла трещина,
– при изготовлении формы возникла трещина,
 – форма забракована.
– форма забракована.
По условию имеем:  ,
,  . Из определения условной вероятности вытекает:
. Из определения условной вероятности вытекает:  . Из условия задачи ясно, что деталь может быть забракована только в случае, если она имеет трещину, т.е.
. Из условия задачи ясно, что деталь может быть забракована только в случае, если она имеет трещину, т.е.  . Следовательно,
. Следовательно,  . По свойству 1 вероятности форма не бракуется с вероятностью
. По свойству 1 вероятности форма не бракуется с вероятностью  .
.
Пусть событие  заключается в том, что
заключается в том, что  -я форма не забракована. Тогда событие
-я форма не забракована. Тогда событие  означает, что обе выбранные формы не забракованы. Так как события
означает, что обе выбранные формы не забракованы. Так как события  и
и  независимы, то
независимы, то  .
.
Решение задачи № 7
Для решения этой задачи нужно изучить раздел «Схема Бернулли» Вероятность того, что событие (в данном случае – попадание в мишень) совершится в  независимых испытаниях точно
независимых испытаниях точно  раз, находится по формуле Бернулли:
раз, находится по формуле Бернулли:  , где
, где  – вероятность того, что событие
– вероятность того, что событие 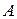 произойдет в одном испытании, а
произойдет в одном испытании, а  .
.
а) Пусть  – исследуемое событие. Используя формулу вероятности суммы несовместных событий, получаем:
– исследуемое событие. Используя формулу вероятности суммы несовместных событий, получаем:

 .
.
б) Пусть  – нужное событие. Имеем:
– нужное событие. Имеем:
 .
.
в) Пусть  – изучаемое событие. Тогда
– изучаемое событие. Тогда  и
и
 .
.
Решение задачи № 8
Для решения этой задачи необходима формула полной вероятности.
Введем полную систему гипотез:
 – извлечен и переложен белый шар;
– извлечен и переложен белый шар;
 – извлечен и переложен черный шар.
– извлечен и переложен черный шар.
Так как в первой урне всего 11 шаров, а среди них 6 белых и 5 черных, то  и
и  . Пусть
. Пусть 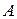 – событие, заключающееся в том, что извлеченный из второй урны шар оказался белым. Если выполнилась гипотеза
– событие, заключающееся в том, что извлеченный из второй урны шар оказался белым. Если выполнилась гипотеза  , то во второй урне стало всего 20 шаров и среди них 5 белых. Поэтому
, то во второй урне стало всего 20 шаров и среди них 5 белых. Поэтому  . Если выполнилась гипотеза
. Если выполнилась гипотеза  , то во второй урне стало всего 20 шаров и среди них 4 белых. Поэтому
, то во второй урне стало всего 20 шаров и среди них 4 белых. Поэтому  . По формуле полной вероятности имеем:
. По формуле полной вероятности имеем:
 .
.
Рекомендации по выполнению заданий 10-11
Теоретический материал и подробное решение типовых задач по теме: «Дискретная случайная величина» можно найти в § 2-6 главы VI; в § 1-5 главы VII (стр.75);, в § 3-7 главы VIII учебника [1] (стр. 85); в § 1–3 главы IV учебного пособия [2].
Решение задачи № 10
В таблице, представляющей собой закон распределения с.в.  , не заполнена одна ячейка во второй строке. Однако известно, что сумма чисел в этой строке должна равняться единице. Таким образом, в этой ячейке запишем число
, не заполнена одна ячейка во второй строке. Однако известно, что сумма чисел в этой строке должна равняться единице. Таким образом, в этой ячейке запишем число  :
:

| -7 | -2 | ||

| 0,1 | 0,3 | 0,25 | 0,35 |
По свойству 4 математического ожидания  равно скалярному произведению 1-й и 2-й строк этой таблицы То есть,
равно скалярному произведению 1-й и 2-й строк этой таблицы То есть,
 .
.
Перейдем к нахождению дисперсии  . Сначала составим закон распределения с.в.
. Сначала составим закон распределения с.в.  :
:

| ||||

| 0,1 | 0,3 | 0,25 | 0,35 |
(тот факт, что в первой строке этой таблицы числа идут не по возрастанию, не влияет на правильность вычислений). Находим  :
:
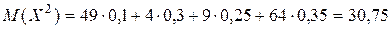 .
.
По свойству 1 дисперсии (формула(21) в лекции 5) имеем:
 .
.
Среднеквадратичное отклонение  вычисляется по формуле:
вычисляется по формуле:
 .
.
Так как с.в.  только четыре значения:
только четыре значения:  , то
, то

Согласно определению 20 функция распределения  с.в.
с.в.  задается равенством:
задается равенством:  . Поэтому:
. Поэтому:
· при 
 ;
;
· при 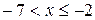
 ;
;
· при 
 ;
;
· при 
 ;
;
· при 
 .
.
Начертить график этой функции самостоятельно!
Рекомендации по выполнению заданий 12-15
1.Теоретический материал и подробное решение типовых задач по теме: «Непрерывная случайная величина» можно найти в § 1-5 главы ХI; в § 1-7 главы ХII, в § 1-4 главы ХIII учебника [1]; и в § 1-6 главы VI учебного пособия [2].
Решение задачи № 12
Если  , то
, то  и первое условие плотности выполняется.
и первое условие плотности выполняется.
Определим, при каком  выполняется второе условие плотности, то есть. Имеем по свойству аддитивности интеграла:
выполняется второе условие плотности, то есть. Имеем по свойству аддитивности интеграла:

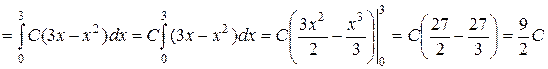 .
.
Итак,  . Таким образом,
. Таким образом,

График данной функции имеет вид:

Математическое ожидание  вычислим по формуле:
вычислим по формуле:

 .
.
Функцию распределения  вычислим по формуле:
вычислим по формуле:  .
.
Если  , то
, то  .
.
Если  , то
, то 
 .
.
Если  , то
, то 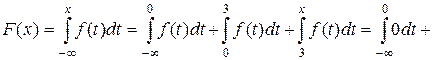
 .
.
Таким образом,

График данной функции имеет вид:

Из свойства аддитивности вероятности следует:
 .
.
 .
.
По формуле  , так как функция
, так как функция  непрерывна (см., например, чертеж). Следовательно,
непрерывна (см., например, чертеж). Следовательно, 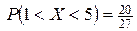 .
.
Решение задачи № 13
Для решения этой задачи надо изучить нормальный закон распределения.
Параметрами данного нормального закона являются числа  (математическое ожидание) и
(математическое ожидание) и  (среднеквадратичное отклонение). Функция распределения
(среднеквадратичное отклонение). Функция распределения  этого закона вычисляется по формуле
этого закона вычисляется по формуле  , где
, где  – затабулированная функция Лапласа. Применяя формулы, а также нечетность функции
– затабулированная функция Лапласа. Применяя формулы, а также нечетность функции  , имеем:
, имеем:

 ;
;

 .
.
Решение задачи № 14
Пусть  – с.в., равная ошибке измерения. Известно, что
– с.в., равная ошибке измерения. Известно, что  , а так как систематических ошибок нет, то
, а так как систематических ошибок нет, то  . Действуя так же, как и в предыдущей задаче, получаем:
. Действуя так же, как и в предыдущей задаче, получаем:

 .
.
Контрольные задания
Вариант 1
1. Пусть Ai – событие (i = 1,2,3,4),состоящее в том, что i-ый компьютер в дисплейном классе выйдет из строя в течение суток. Выразить через события Ai следующие события:
а) А - хотя бы один компьютер выйдет из строя в течение суток,
б) В - ни один не выйдет из строя,
в) С - 3 компьютера выйдут из строя.
2. Брошены 3 игральные кости. Найти вероятность того, что
а) на каждой из выпавших граней появится 5 очков,
б) на всех выпавших гранях появится одинаковое число очков,
в) сумма выпавших очков не превысит 6.
3. В ящике имеется 24 детали, среди которых 13 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 1 бракованная и 2 качественные.
4. В электросеть включены лампочки, соединенные между собой следующим образом:
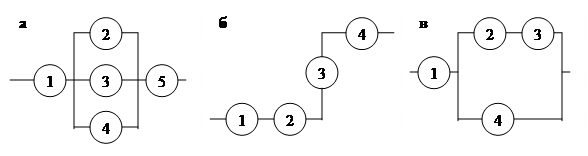 |
Ai – работа i-й лампочки, i = 1, 2, 3, 4, 5.
P(A 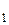 )=0,6; P(A
)=0,6; P(A 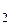 )=0,7; P(A
)=0,7; P(A  )=0,8; P(A
)=0,8; P(A 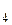 )=0,5; P(A
)=0,5; P(A  )=0,9.
)=0,9. 
Найти вероятность безотказной работы цепи.
5. Для сигнализации об аварии в системе установлены три независимо работающих сигнализатора. Вероятности того, что в момент аварии сработает 1-й сигнализатор = 0,8, 2-й = 0,7, 3-й = 0,9. Найти а) вероятность того, что в случае аварии сработает хотя бы один сигнализатор, б) все три сигнализатора.
6. Вероятность того, что студент сдаст первый экзамен, равна 0,7; второй –0,6; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только первый экзамен, б) по крайней мере два экзамена, в) все три экзамена.
7. Вероятность попадания стрелком в мишень при одном выстреле равна 0,6. Найти вероятность того, что при шести выстрелах стрелок попадет:
а) не более 3 раз, б) ни одного раза, в) хотя бы один раз.
8. В первой урне содержится 11 шаров, из них 3 белых, во второй урне 16 шаров, из них 2 белых. Из первой урны наудачу извлекли один шар и переложили во вторую. Найти вероятность того, что извлеченный после этого из второй урны шар окажется белым.
9. На стройку поступают изделия трех заводов. Первый завод поставляет 10% всех изделий, второй-30%. третий-60%. Вероятность того, что изделие качественное равны для 1-го завода 0,9, для 2-го-0,85, для З-го-0,8. Наудачу взятое изделие оказалось бракованным. Найти вероятность того, что оно изготовлено на 2-м заводе.
10. Найти F(x), M(X), D(X), 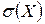 , P(2<X<7)
, P(2<X<7)
| Х | -1 | |||
| Р | 0,25 | 0,2 | 0,45 |
11. Магазин получил 2000 бутылок молока. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Составить закон распределения с.в. Х- числа разбитых бутылок, пренебрегая значениями Х, вероятность которых меньше 0,005. Найти M(X), D(X), 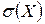 .
.
12. Дана плотность распределения непрерывной случайной величины

Найти c, F(x), M(Х), построить графики f(х), F(x).
13. С.в. распределена по нормальному закону с плотностью:

Найти Р(-2<X<-1), Р(-6  X
X  3).
3).
14. Производится взвешивание коробок конфет без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со среднеквадратичным отклонением - 12 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 15 г.
15. Вероятность попадания в цель при одном выстреле из орудия равна 0,7. Найти вероятности того, что из 300 выстрелов число попаданий будет
а) не менее 150, б) между 170 и 250, в) более 200.
Вариант 2
1. На заводе изделия изготавливаются на четырех станках. Обозначим через А  – событие (i = 1,2,3,4), состоящее в том, что изделие, изготовленное на i-м станке является бракованным. Выразить через события A
– событие (i = 1,2,3,4), состоящее в том, что изделие, изготовленное на i-м станке является бракованным. Выразить через события A  следующие события:
следующие события:
а) А - все четыре изделия бракованные,
б) В - ни одно изделие не бракованное,
в) С - хотя бы одно изделие бракованное.
2. Брошены 2 игральные кости. Найти вероятность следующих событий:
а) сумма выпавших очков равна 4,
б) сумма очков равна 5, а произведение 6,
в) сумма очков не превышает 7,
г) разность очков меньше 3,
д) сумма очков расположена в промежутке [3;6].
3. В ящике имеется 16 деталей, среди которых 4 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 2 бракованные.
4. В электросеть включены лампочки, соединенные между собой следующим образом:
 |
Ai – работа i-й лампочки, i = 1, 2, 3, 4, 5, 6.
P(A  )=0,5; P(A
)=0,5; P(A  )=0,7; P(A
)=0,7; P(A  )=0,6; P(A
)=0,6; P(A  )=0,85; P(A
)=0,85; P(A  )=0,9; P(A
)=0,9; P(A  )=0,75.
)=0,75. 
Найти вероятность безотказной работы цепи.
5. Независимо друг от друга работают три сигнализатора, установленные в данной системе. Вероятности того, что в момент аварии сработает 1-й сигнализатор = 0,8, 2-й = 0,9, 3-й = 0,9. Найти вероятность того, что в случае аварии сработают не менее двух сигнализаторов.
6. Вероятность попадания в цель при стрельбе из трех орудий равна соответственно 0,7; 0,8; 0,6. Какова вероятность того, что при одном залпе в мишень попадет только один стрелок.
7. Обычную монету бросили 10 раз. Какова вероятность, что при этом герб
выпал:
а) не более 4 раз, б) ни одного раза, в) хотя бы один раз.
8. В первой урне содержится 18 шаров, из них 8 белых, во второй урне 16 шаров, из них 7 белых. Из первой урны наудачу извлекли один шар и переложили во вторую. Найти вероятность того, что извлеченный после этого из второй урны шар окажется белым.
9. Часы, поступающие в магазин, производятся тремя заводами: с первого поступает 70%, со второго-20%, с третьего-10% всех изделий. Процент брака на каждом из заводов составляет соответственно 3%, 2% и 4%. Найти: 1) вероятность того, что купленные часы бракованные; 2) вероятность того, что эти бракованные часы изготовлены на 2-м заводе.
10. Найти F(x), M(X), D(X), σ(X), P(1<X<7)
| Х | -1 | |||
| Р | 0,2 | 0,25 | 0,1 |
11. Магазин получил 2000 бутылок молока. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Составить закон распределения с.в. Х- числа разбитых бутылок, пренебрегая значениями Х, вероятность которых меньше 0,005. Найти M(X), D(X), 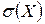 .
.
12. Найти M(Х), D(X), если задана функция распределения
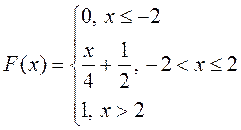
13. С.в. распределена по нормальному закону с плотностью:

Найти Р(-2<X<-1), Р(-6  X
X  3).
3).
14. При изготовлении детали допускается случайная ошибка со среднеквадратичным отклонением - 0,1 см. Найти вероятность того, что деталь изготовлена с ошибкой не превосходящей по абсолютной по абсолютной величине 10,3 см.
15. Автомат изготавливает одинаковые изделия. Вероятность того, что наудачу взятая деталь имеет отличное качество равна 0,7. Найти вероятность того, что в партии из 1000 изделий деталей отличного качества окажется: а) не менее 500, б) между 600 и 900, в) более 700.
Вариант 3
1. Проводятся три испытания прибора. Аi – событие (i=1,2,3,4), состоящее в том, что при i-м испытании прибор выйдет из строя. Выразить через события Аi следующие события:
а) А - прибор выйдет из строя при двух испытаниях;
б) В - прибор не выйдет из строя;
в) С - прибор выйдет из строя хотя бы при одном испытании.
2. Брошены 2 игральные кости. Найти вероятность следующих событий
а) сумма выпавших очков равна 7,
б) сумма очков равна 10, а произведение 24,
в) разность очков меньше 3,
г) сумма очков расположена в промежутке [7;9].
3. В ящике имеется 9 деталей, среди которых 2 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 1 бракованная.
4. В электросеть включены лампочки, соединенные между собой следующим образом:
 | 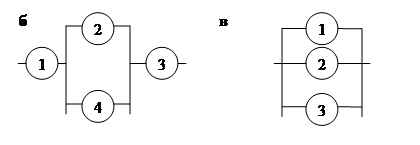 |
Ai – работа i-й лампочки, i = 1, 2, 3, 4.
P(A 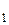 )=0,6; P(A
)=0,6; P(A 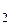 )=0,7; P(A
)=0,7; P(A  )=0,8; P(A
)=0,8; P(A 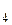 )=0,5.
)=0,5. 
Найти вероятность безотказной работы цепи.
5. В карьере работает 3 экскаватора, загруженных на 70% каждый. Найти вероятность того, что прибывший автомобиль застанет хотя бы один экскаватор свободным. Какова вероятность того, что в этот момент свободны точно 2экскаватора.
6. Станция скорой медицинской помощи имеет три реанимационные бригады. Вероятность того, что в любой момент времени заняты: 1-я бригада равна 0,5, 2-я – 0,6, 3-я – 0,7. Найти вероятность того, что в случайный момент времени все бригады заняты.
7. Вероятность попадания стрелком в мишень при одном выстреле равна 0,6, Найти вероятность того, что при четырех выстрелах стрелок попадет:
а) не более 3 раз, б) ни одного раза, в) хотя бы 2раза.
8.В первой урне содержится 11 шаров, из них 4 белых, во второй урне 12 шаров, из них 2 белых. Из первой урны наудачу извлекли один шар и переложили во вторую. Найти вероятность того, что извлеченный после этого из второй урны шар окажется белым.
9. Детали изготавливаются на двух заводах, причем первый завод выпускает 70%, а второй 30%. Вероятность того, что деталь окажется бракованной равна 0,2, если она сделана на первом заводе, и 0,3, если на втором. Найти вероятность того, что наудачу взятая качественной деталь окажется качественной.
10. Найти F(x), M(X), D(X), σ(X), P(3<X<7)
| Х | -1 | |||
| Р | 0,2 | 0,1 | 0,3 |
11. Вероятность попадания в цель при каждом выстреле равна 0,002. Производится 2000 выстрелов. Составить закон распределения с.в.Х - числа попаданий в цель, пренебрегая значениями X, вероятность которых меньше 0,005. Найти M(X), D(X), σ(X).
12. Дана плотность распределения непрерывной случайной величины

13. С.в. X распределена по нормальному закону с плотностью:
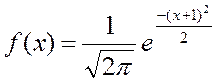
Найти 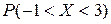 ,
,  .
.
14. Размер детали задан полем допуска 10-12 мм. Оказалось, что средний размер деталей равен 11,4 мм., а среднеквадратичное отклонение равно 0,7 мм. Считая, что размер детали подчиняется закону нормального распределения, определить вероятность появления брака.
15. Имеется 100 станков одинаковой мощности, работающих независимо друг от друга в одинаковом режиме, при котором их привод оказывается включенным в течение 0,8 всего рабочего времени. Какова вероятность того, что в произвольный момент времени окажутся включенными от 70 до 86 станков. Найти вероятность того, что включенными окажутся более 64 станков.
Вариант 4
1. Брошено 5 монет. Обозначим через Ai-событие, состоящее в том, что при бросании i-ой монеты (1,2,3,4,5) выпадет «герб». Выразить через Ai следующие события:
А - «герб» выпадет только один раз,
Б - «герб» выпадет хотя бы один раз,
С - «герб» не выпадет ни разу.
2. Брошены 2 игральные кости. Описать пространство элементарных событий и найти вероятности- следующих событий:
а) сумма выпавших очков равна 8,
б) сумма очков равна 6, а произведение 8,
в) сумма очков не превышает 4,
г) разность очков меньше 2,
д) сумма очков расположена в промежутке [ 2,4 ].
3. В ящике имеется 18 деталей, среди которых 6 бракованных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 3 бракованных.
- В электросеть включены лампочки, соединенные между собой следующим образом:
 б)
б)
 а) в)
а) в)


























 Найти вероятность безотказной работы цепи, если
Найти вероятность безотказной работы цепи, если
Ai – работа i-й лампочки, i = 1, 2, 3, 4, 5, 6, 7,
P(A  )=0,6; P(A
)=0,6; P(A  )=0,7; P(A
)=0,7; P(A  )=0,8; P(A
)=0,8; P(A  )=0,5, P(A5)=0,9, P(A6)=0,6, P(A7)=0,7.
)=0,5, P(A5)=0,9, P(A6)=0,6, P(A7)=0,7.