Построение корпуса Чебышева
Корпус Чебышева представляет собой 9 теоретических шпангоутов, построенных на оба борта.
Чебышевские шпангоуты строятся по абсциссам, которые вычисляются по формулам:
х1= -х9=0,9116*1 = 0,9116*48,16=43902м;
х2= -х8=0,6010*1 = 0,6010*48,16=28944м;
х3= -х7=0,5288*1 =0,5288*48,16=25467 м;
х4= -х6=0,1679*1 = 0,1679*48,16=8086 м;
х5= 0 м,
где l – чебышевская шпация.
При Lc>0,15L:
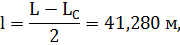
где Lc=41,280м – длина симметрично расположенной цилиндрической вставки.
На рисунке 1 листа 45.079-010-04 построен корпус Чебышева.
Проведение равнообъёмных ватерлиний и расчёт метацентрического радиуса
Расчёт производится по формулам:
I 
II 
III 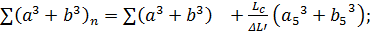
IV 
V 
VI 
VII 
VIII 
где a,b – ординаты вспомогательной ватерлинии, замеряемые по корпусу Чебышева от центра тяжести предыдущей равнообъёмной ватерлинии;
n=9 – количество чебышевских шпангоутов;
 – чебышевский промежуток;
– чебышевский промежуток;
a5,b5 – ординаты вспомогательной ватерлинии на границах цилиндрической вставки, то есть ординаты мидель-шпангоута.
Метацентрический радиус в таблице 3 - Вычисление метацентрического радиуса по ординатам вспомогательных ватерлиний, прежде всего, рассчитывается при плавании судна по начальную ватерлинию КВЛ при угле крена θ=0°. Затем через центр тяжести начальной ватерлинии точку F0 под углом ∆θ.
На рисунке 1приведена кривая метацентрического радиуса.
| L | 137,6 | Длина по КВЛ, м | ||||||
| Lc | 41,28 | Длина симметричной цилиндрической вставки, м | ||||||
| ΔL' | 10,702 | |||||||
| V0 | Водоизмещение, м³ | |||||||
| zg | 3,8 | Аппликата центра тяжести, м | ||||||
| zc | 1,76 | Аппликата центра величины, м | ||||||
| a0 | 2,04 | Возвышение центра тяжести над центром величины, м | ||||||
| ΔL | 6,88 | |||||||
| Xc | Абсцисса центра величины | |||||||
| Mo |
| Таблица 3 Вычисление метацентрического радиуса по ординатам вспомогательных ватерлиний | ||||||||||||||||||
| θk | ||||||||||||||||||
| № шп | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ |
| 4,43 | 4,43 | 19,6 | 19,6 | 86,9 | 86,9 | 4,58 | 4,31 | 18,6 | 95,9 | 80,1 | 4,78 | 4,16 | 22,9 | 17,3 | ||||
| 8,05 | 8,05 | 64,8 | 64,8 | 8,14 | 8,06 | 66,2 | 64,9 | 8,29 | 8,06 | 68,6 | 64,9 | |||||||
| 8,23 | 8,23 | 67,7 | 67,7 | 8,28 | 8,26 | 68,6 | 68,3 | 8,4 | 8,32 | 70,5 | 69,2 | |||||||
| 8,41 | 8,41 | 70,7 | 70,7 | 8,4 | 8,49 | 70,5 | 8,49 | 8,59 | 73,9 | |||||||||
| 8,41 | 8,41 | 70,7 | 70,7 | 8,4 | 8,49 | 70,5 | 8,49 | 8,59 | 73,9 | |||||||||
| 8,41 | 8,41 | 70,7 | 70,7 | 8,37 | 8,49 | 8,49 | 8,59 | 73,9 | ||||||||||
| 8,23 | 8,23 | 67,7 | 67,7 | 8,31 | 8,36 | 69,9 | 8,48 | 8,35 | 71,9 | 69,7 | ||||||||
| 8,22 | 8,22 | 67,6 | 67,6 | 8,14 | 8,16 | 66,2 | 66,6 | 8,44 | 8,05 | 71,3 | 64,7 | |||||||
| 5,48 | 5,48 | 5,99 | 5,01 | 35,9 | 25,1 | 6,56 | 4,49 | 20,1 | 90,2 | |||||||||
| I | 200,61 | 201,35 | 203,47 | |||||||||||||||
| II | 0,00 | 3,07 | 29,62 | |||||||||||||||
| III | 13043,17 | 13197,98 | 13668,43 | |||||||||||||||
| IV | 0,00 | 0,01 | 0,07 | |||||||||||||||
| V | 46530,31 | 47082,57 | 48760,84 | |||||||||||||||
| VI | 0,00 | 0,12 | 11,53 | |||||||||||||||
| VII | 46530,31 | 47082,44 | 48749,31 | |||||||||||||||
| VIII | 6,83 | 6,91 | 7,15 | |||||||||||||||
| Продолжение таблицы | ||||||||||||||||||
| θk | ||||||||||||||||||
| № шп | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ |
| 4,98 | 4,09 | 24,8 | 16,7 | 68,3 | 5,24 | 4,04 | 27,4 | 16,4 | 66,1 | 5,91 | 3,73 | 13,9 | 51,8 | |||||
| 8,43 | 8,14 | 71,1 | 66,2 | 8,04 | 8,16 | 64,6 | 66,5 | 5,91 | 7,09 | 50,3 | ||||||||
| 8,51 | 8,46 | 72,4 | 71,6 | 8,04 | 8,49 | 64,6 | 5,91 | 7,1 | 50,4 | |||||||||
| 8,58 | 8,83 | 73,6 | 8,04 | 9,08 | 64,6 | 82,4 | 5,91 | 7,1 | 50,4 | |||||||||
| 8,58 | 8,83 | 73,6 | 8,04 | 9,15 | 64,6 | 83,8 | 5,91 | 7,1 | 50,4 | |||||||||
| 8,58 | 8,83 | 73,6 | 8,04 | 9,02 | 64,6 | 81,4 | 5,91 | 7,1 | 50,4 | |||||||||
| 8,58 | 8,27 | 73,6 | 68,4 | 8,04 | 8,02 | 64,6 | 64,4 | 5,91 | 6,82 | 46,6 | ||||||||
| 8,56 | 7,88 | 73,2 | 62,1 | 8,04 | 7,56 | 64,6 | 57,2 | 5,91 | 6,46 | 41,7 | ||||||||
| 7,08 | 4,08 | 50,2 | 16,6 | 67,9 | 7,57 | 3,75 | 57,3 | 14,1 | 52,9 | 5,91 | 3,06 | 9,36 | 28,6 | |||||
| I | 206,46 | 202,65 | 158,95 | |||||||||||||||
| II | 33,42 | -75,21 | -107,74 | |||||||||||||||
| III | 14344,82 | 13642,05 | 6490,79 | |||||||||||||||
| IV | 0,08 | -0,19 | -0,34 | |||||||||||||||
| V | 51173,83 | 48666,76 | 23155,30 | |||||||||||||||
| VI | 14,48 | 74,68 | 195,39 | |||||||||||||||
| VII | 51159,35 | 48592,08 | 22959,91 | |||||||||||||||
| VIII | 7,51 | 7,13 | 3,37 | |||||||||||||||
| Продолжение таблицы | ||||||||||||||||||
| θk | ||||||||||||||||||
| № шп | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ |
| 4,96 | 3,27 | 24,6 | 10,7 | 34,9 | 4,24 | 3,2 | 10,2 | 76,1 | 32,6 | 3,77 | 3,24 | 14,2 | 10,5 | 53,6 | ||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,3 | 24,6 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | |||||
| 4,96 | 5,23 | 24,6 | 27,4 | 4,24 | 4,43 | 19,6 | 76,1 | 86,9 | 3,77 | 3,93 | 14,2 | 15,4 | 53,6 | 60,5 | ||||
| 4,96 | 2,42 | 24,6 | 5,84 | 14,1 | 4,24 | 2,22 | 4,91 | 76,1 | 10,9 | 3,77 | 2,13 | 14,2 | 4,55 | 53,6 | 9,7 | |||
| I | 126,90 | 107,97 | 96,46 | |||||||||||||||
| II | -3,92 | 2,71 | 0,43 | |||||||||||||||
| III | 3226,18 | 1964,75 | 1389,14 | |||||||||||||||
| IV | -0,02 | 0,01 | 0,00 | |||||||||||||||
| V | 11509,11 | 7009,05 | 4955,61 | |||||||||||||||
| VI | 0,32 | 0,18 | 0,01 | |||||||||||||||
| VII | 11508,79 | 7008,87 | 4955,61 | |||||||||||||||
| VIII | 1,69 | 1,03 | 0,73 | |||||||||||||||
| Продолжение таблицы | ||||||||||||||||||
| θk | ||||||||||||||||||
| № шп | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ | a | b | a² | b² | a³ | b³ |
| 3,49 | 3,33 | 12,2 | 11,1 | 42,5 | 3,33 | 3,42 | 11,1 | 11,7 | 36,8 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | |||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 3,62 | 12,2 | 13,1 | 42,5 | 47,3 | 3,33 | 3,46 | 11,1 | 36,8 | 41,5 | 3,26 | 3,43 | 10,6 | 11,8 | 34,6 | 40,3 | ||
| 3,49 | 2,12 | 12,2 | 4,5 | 42,5 | 9,56 | 3,33 | 2,19 | 11,1 | 4,81 | 36,8 | 10,5 | 3,26 | 2,36 | 10,6 | 5,55 | 34,6 | 13,1 | |
| I | 89,58 | 85,96 | 84,88 | |||||||||||||||
| II | -1,13 | -4,24 | -8,50 | |||||||||||||||
| III | 1106,34 | 974,11 | 934,94 | |||||||||||||||
| IV | -0,01 | -0,02 | -0,05 | |||||||||||||||
| V | 3946,78 | 3475,03 | 3335,31 | |||||||||||||||
| VI | 0,04 | 0,56 | 2,28 | |||||||||||||||
| VII | 3946,74 | 3474,48 | 3333,03 | |||||||||||||||
| VIII | 0,58 | 0,51 | 0,49 |

Вычисление координат центра величины и поперечного метацентра
На конечных углах крена центр величины меняет своё положение. Координаты центра величины и поперечного метацентра рассчитаны в таблице 4 по формулам:
для координат центра величины:

где Δθ – угловой промежуток, рад;
для координат поперечного метацентра:
 .
.
| Таблица 4 Вычисление координат центра величины и метацентра | |||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X |
| θ° | r | r cosθ | Σ r cosθ | yc=Δθ/2(IV) | r sinθ | Σ r sinθ | zc-zc0= Δθ/2(VII) | ym=(V)-(VI) | zm-zc0= (VIII)+(III) |
| 6,83 | 6,83 | 6,83 | |||||||
| 6,91 | 6,884 | 13,71 | 0,598 | 0,602 | 0,602 | 0,026 | -0,004 | 6,91 | |
| 7,15 | 7,041 | 27,64 | 1,206 | 1,242 | 2,446 | 0,107 | -0,036 | 7,148 | |
| 7,51 | 7,254 | 41,93 | 1,83 | 1,944 | 5,631 | 0,246 | -0,114 | 7,5 | |
| 7,13 | 6,7 | 55,89 | 2,439 | 2,439 | 10,01 | 0,437 | -1E-05 | 7,137 | |
| 5,25 | 4,758 | 67,35 | 2,939 | 2,219 | 14,67 | 0,64 | 0,72 | 5,398 | |
| 3,37 | 2,919 | 75,02 | 3,274 | 1,685 | 18,57 | 0,81 | 1,589 | 3,729 | |
| 2,53 | 2,072 | 80,01 | 3,491 | 1,451 | 21,71 | 0,947 | 2,04 | 3,02 | |
| 1,69 | 1,295 | 83,38 | 3,638 | 1,086 | 24,25 | 1,058 | 2,552 | 2,353 | |
| 1,36 | 0,962 | 85,64 | 3,737 | 0,962 | 26,3 | 1,147 | 2,775 | 2,109 | |
| 1,03 | 0,662 | 87,26 | 3,807 | 0,789 | 28,05 | 1,224 | 3,018 | 1,886 | |
| 0,88 | 0,505 | 88,43 | 3,858 | 0,721 | 29,56 | 1,29 | 3,138 | 1,794 | |
| 0,73 | 0,365 | 89,3 | 3,896 | 0,632 | 30,91 | 1,349 | 3,264 | 1,714 | |
| 0,65 | 0,275 | 89,94 | 3,924 | 0,589 | 32,13 | 1,402 | 3,335 | 1,677 | |
| 0,58 | 0,198 | 90,41 | 3,945 | 0,545 | 33,27 | 1,451 | 3,4 | 1,65 | |
| 0,54 | 0,14 | 90,75 | 3,96 | 0,522 | 34,33 | 1,498 | 3,438 | 1,638 | |
| 0,51 | 0,089 | 90,98 | 3,97 | 0,502 | 35,36 | 1,543 | 3,467 | 1,631 | |
| 0,5 | 0,044 | 91,11 | 3,975 | 0,498 | 36,36 | 1,586 | 3,477 | 1,63 | |
| 0,49 | 3E-17 | 91,15 | 3,977 | 0,49 | 37,34 | 1,629 | 3,487 | 1,629 |