В металле электроны проводимости находятся на расстоянии 1-3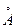 
друг относительно друга, проходят расстояния от 
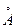(при комнатной температуре) до 10 см (при 1 
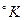) не сталкиваясь. Столь большой пробег обусловлен двумя обстоятельствами. Первое – принцип Паули (рис. 3.6) второе – экранирование кулоновского взаимодействия.
Рис. 3.6. Схема столкновения двух электронов с волновыми векторами 
. После столкновения электроны имеют волновые векторы 
. Принцип Паули допускает лишь такие столкновения, в которых конечные состояния были бы до столкновения вакантными.
Оценим влияние принципа Паули в случае двухчастичного столкновения (рис. 3.7):
1+2 → 3+4.
Эта схема описывает столкновение электрона в возбужденном состоянии 1 с электроном в состоянии 2 внутри сферы Ферми. Удобно отсчитывать энергию от уровня Ферми 
, приняв его за нулевой. Тогда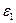 
будет положительной, а 
- отрицательной величиной. Согласно принципу Паули состояния 3 и 4 электронов после столкновения должны находиться вне сферы Ферми, поскольку все состояния внутри сферы уже заняты. Следовательно, энергии 
и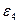 
должны быть положительными (рис. 3.7).
Рис. 3.7. Пояснение процесса столкновения двух электронов.
Закон сохранения энергии требует, чтобы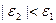 
, так как в противном случае условие 
(где обе стороны положительны) не может быть выполнено. Это означает, что столкновения возможны в том случае, если состояние 2 лежит внутри слоя толщиной 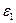внутри поверхности Ферми. Подходящей мишенью для электрона 1 является не любой электрон, а лишь электрон из заполненного слоя, в котором число электронов составляет долю 
всего их числа. Даже если электрон-мишень 2 находится в нужном слое, лишь небольшая часть конечных состояний совместима с законами сохранения энергии и импульса и допустима по принципу Паули. Это обстоятельство еще уменьшает допустимое количество на множитель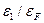 
. На рис. 3.7 показана малая сфера, на поверхности которой все пары состояний 3, 4 на противоположных концах диаметра удовлетворяют требованиям закона сохранения, но столкновения возможны только такие, в результате которых оба состояния 3, 4 оказываются вне сферы Ферми. В результате понижающий множитель равен 
. Множитель 
и есть фактор, характеризующий уменьшение частоты столкновений, вызванного влиянием принципа Паули.
Если 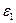порядка 
, то уменьшение частоты электрон-электронных столкновений относительно классической величины будет характеризоваться множителем 
, а для эффективного сечения столкновений получим выражение
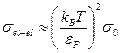, (3.26)
где 
- сечение для экранирования кулоновского взаимодействия. Взаимодействие одного электрона с другим имеет порядок длины экранирования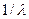 
. Численные расчеты показывают, что эффективное сечение столкновения между электронами с учетом экранирования порядка 
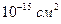. Однако наибольшее уменьшение связано с влиянием принципа Паули .
При комнатной температуре 
, а следовательно 
. Средняя длина свободного пробега при комнатной температуре для электрон-электронных столкновений равна по порядку величины 
(
). Эта величина на порядок больше, чем средняя длина свободного пробега для электрон-фононного взаимодействия при комнатной температуре. Это значит, что электроны сталкиваются преимущественно с фононами.
Таким образом, принцип Паули дает ответ на один из центральных вопросов теории металлов: почему электроны проходят в металле такие большие расстояния, не сталкиваясь между собой.