Министерство Образования Республики Беларусь
Белорусский национальный технический университет
Кафедра: «Машины и технологии литейного производства»
Курсовой проект
на тему:
1. «Алгоритмизация и программирование разветвляющихся процессов».
2. «Методы решения нелинейных уравнений».
Вариант №8
Выполнил: студент гр.104319
Елак И.М.
Руководитель: профессор
Чичко А.Н.
Минск 2011г.
Постановка задачи 1. Разработать алгоритм и программу формирования одномерного массива Z[i] по условию Z[i]=Z(x), заданной интервально на различных промежутках. Если функция Z(x) неопределенна при каких-либо значениях x, то в программе необходимо предусмотреть вывод сообщения «При данном Х функция неопределенна» и вывести значение Х. Вид задания функции:
| Z(x)= | F20 x≤x20 | , x20=20-12, | |
| F21 x12<x≤x21 | , x21=21-12, | ||
| F23 x21<x≤x23 | , x23=23-12, | ||
| F24 x23<x≤x24 | , x24=24-12, | ||
| F25 x24<x≤x25 | , x25=25-12, | ||
| 0, x>x25 | . |
где
f 20=Z*x3Z +b*ln3x -  +c*lnx-c;
+c*lnx-c;
f21 =ln(Zx) + cos(xb)/ln(bx) - (x+7d)+c 
f23 =ln(cos(Zx)) + b2ebx - cx5+ 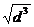 ln
ln  ;
;
f24 =e-cx/3+Z*ln(Zx)+b  - d/(x3+7)
- d/(x3+7)
f25 =Z*ln3/8  + b*sin(be-b/x)+(x-c)+d
+ b*sin(be-b/x)+(x-c)+d  .
.
Значения Z,b,c,d вычисляются по формулам:
 ,
, 
 ,
,
 ,
, 
 , где n – номер варианта.
, где n – номер варианта.
При формировании функции массива Z[i] можно выбрать несколько вариантов шага, но при условии, чтобы на каждом из интервалов было взято не менее 10-ти значений
При выполнении задачи шаг по x можно брать нецелым числом. В программе необходимо организовать вывод всех элементов Z[i] и числа их значений на монитор.
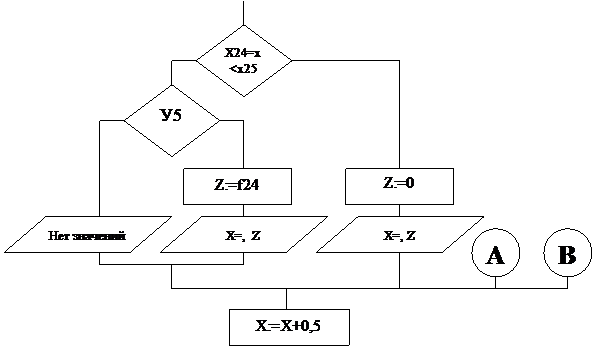
Блок-схема для задачи 1.
|







 | |||||||||
 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||
 | |||






 |
Программа задачи №1.
ProgrZm ZZdZchZ1;
uses crt;
vZr j:integer;
Z,b,c,d,x,z,z1, x20,x21,x23,x24,x25:reZl;
i,n:integer;
f:text;
Begin
clrscr;
Zssign(f,'result8.txt');
rewrite(f);
Z:=0;b:=0;c:=0;n:=8;
for j:=1 to n+3 do begin
Z:=Z+sin(j); b:=b+ln(j); c:=c+j*j*j+j; end;
d:=Z+b+c;
x20:=20-12; x21:=21-12; x23:=23-12; x24:=24-12; x25:=25-12;
x:=0
for i:=1 to 300 do begin
if x<=x20 then begin
if (x>0) Znd (ln(x)>0) Znd ((d*x)>=0) then begin
z:=Z*exp(3*Z*ln(x))+b*exp(3*ln(ln(x)))+sqrt(d*x)+(-c)*c*ln(x);
writeln(f,'x=',x:6:2,' Z=',z:12:3);
end
else writeln(f,'x=',x:6:2,' Z=net znZcheniy');
end;
if (x20<x) Znd (x<=x21) then begin
if ((Z*x)>0) Znd (x>0) Znd ((x*ln(b)<>0)) Znd ((c*exp((2/7)*ln(x)))>0)
Znd (ln(c*exp((2/7)*ln(x)))<>0) then
begin
z:=ln(Z*x)+cos(exp(b*ln(x)))/(x*ln(b))-(x+7*d)+c*exp(2*c*x)/ln(c*exp((2/7)*ln(x)));
writeln(f,'x=',x:6:2,' Z=',z:12:3);end
else
writeln(f,'x=',x:6:2,' Z=net znZcheniy');
end;
if (x21<x) Znd (x<=x23) then begin
if ((cos(Z*x))>0) Znd (d>0) Znd ((exp(3*ln(d)))>0) Znd (x<>0) then
begin
z:=ln(cos(Z*x))+sqrt(b)*exp(b*x)-c*x*exp(4*ln(Zbs(x)))+sqrt(exp(3*ln(d)))*ln(Zbs(x));
writeln(f,'x=',x:6:2,' Z=',z:12:3); end
else
writeln(f,'x=',x:6:2,' Z=net znZcheniy');
end;
if (x23<x) Znd (x<=x24) then begin
if ((Z*x)>0) Znd ((x*exp(2*ln(Zbs(x)))+7)<>0) Znd (x<>0) then
begin
z:=exp((-c)*x/3)+Z*ln(Z*x)+b*sqrt(sqr(sqr(b))*cos(x))-d/(x*exp(2*ln(Zbs(x)))+7);
writeln(f,'x=',x:6:2,' Z=',z:12:3);
end
else
writeln(f,'x=',x:6:2,' Z=net znZcheniy');
end;
if (x24<x) Znd (x<=x25) then begin
if (x<>0) Znd ((ln(Zbs(x)))>0) Znd ((x-d)>0) Znd (ln(x-d)<>0) Znd (cos(x*exp(2*ln(Zbs(x))))<>0) then
begin
z1:=Z*exp((3/8)*ln(ln(Zbs(x))))+b*sin(b*exp((-b)/x))+(x-c);
z:=z1+d*(sqr((sin(x*exp(2*ln(Zbs(x)))))/cos(x*exp(2*ln(Zbs(x))))))/ln(x-d);
writeln(f,'x=',x:6:2,' Z=',z:12:3);
end
else
writeln(f,'x=',x:6:2,' Z=net znZcheniy');
end;
if x>x25 then begin
z:=0;
writeln(f,'x=',x:6:2,' Z=',z:1:0);end;
x:=x+0.5;
end;
End.
Результаты задачи №1.
x= 1.10 Z[23]=-1863632.899
x= 1.15 Z[24]=-2732844.769
x= 1.20 Z[25]=-3565057.423
x= 1.25 Z[26]=-4363292.513
x= 1.30 Z[27]=-5130216.009
x= 1.35 Z[28]=-5868191.921
x= 1.40 Z[29]=-6579326.248
x= 1.45 Z[30]=-7265503.209
x= 1.50 Z[31]=-7928415.330
x= 1.55 Z[32]=-8569588.596
x= 1.60 Z[33]=-9190403.611
x= 1.65 Z[34]=-9792113.493
x= 1.70 Z[35]=-10375859.109
x= 1.75 Z[36]=-10942682.091
x= 1.80 Z[37]=-11493536.019
x= 1.85 Z[38]=-12029296.079
x= 1.90 Z[39]=-12550767.423
x= 1.95 Z[40]=-13058692.451
x= 2.00 Z[41]=-13553757.164
x= 2.05 Z[42]=-14036596.739
x= 2.10 Z[43]=-14507800.426
x= 2.15 Z[44]=-14967915.874
x= 2.20 Z[45]=-15417452.956
x= 2.25 Z[46]=-15856887.165
x= 2.30 Z[47]=-16286662.639
x= 2.35 Z[48]=-16707194.855
x= 2.40 Z[49]=-17118873.048
x= 2.45 Z[50]=-17522062.371
x= 2.50 Z[51]=-17917105.846
…………………………………
x= 7.60 Z[153]=-39658246.466
x= 7.65 Z[154]=-39786468.362
x= 7.70 Z[155]=-39913854.919
x= 7.75 Z[156]=-40040416.951
x= 7.80 Z[157]=-40166165.062
x= 7.85 Z[158]=-40291109.654
x= 7.90 Z[159]=-40415260.931
x= 7.95 Z[160]=-40538628.903
x= 8.00 Z[161]= -31086.240
x= 8.05 Z[162]= -31086.215
x= 8.10 Z[163]= -31086.332
x= 8.15 Z[164]= -31086.355
x= 8.20 Z[165]= -31086.337
x= 8.25 Z[166]= -31086.384
x= 8.30 Z[167]= -31086.464
x= 8.35 Z[168]= -31086.469
x= 8.40 Z[169]= -31086.592
x= 8.45 Z[170]= -31086.559
x= 8.50 Z[171]= -31086.627
x= 8.55 Z[172]= -31086.648
x= 8.60 Z[173]= -31086.737
x= 8.65 Z[174]= -31086.812
x= 8.70 Z[175]= -31086.845
x= 8.75 Z[176]= -31086.841
x= 8.80 Z[177]= -31086.884
…………………………………
x= 9.40 Z[189]=net znZcheniy
x= 9.45 Z[190]=net znZcheniy
x= 9.50 Z[191]=net znZcheniy
x= 9.55 Z[192]=net znZcheniy
x= 9.60 Z[193]=net znZcheniy
x= 9.65 Z[194]=net znZcheniy
x= 9.70 Z[195]=net znZcheniy
x= 9.75 Z[196]=net znZcheniy
x= 9.80 Z[197]=net znZcheniy
x= 9.85 Z[198]=net znZcheniy
x= 9.90 Z[199]=net znZcheniy
x= 9.95 Z[200]=net znZcheniy
x= 10.00 Z[201]=net znZcheniy
x= 10.05 Z[202]=net znZcheniy
x= 10.10 Z[203]=net znZcheniy
x= 10.15 Z[204]=net znZcheniy
x= 10.20 Z[205]=net znZcheniy
x= 10.25 Z[206]=net znZcheniy
x= 10.30 Z[207]=net znZcheniy
x= 10.35 Z[208]=net znZcheniy
x= 10.40 Z[209]=net znZcheniy
x= 10.45 Z[210]=net znZcheniy
x= 10.50 Z[211]=net znZcheniy
x= 10.55 Z[212]=net znZcheniy
x= 10.60 Z[213]=net znZcheniy
x= 10.65 Z[214]=net znZcheniy
x= 10.70 Z[215]=net znZcheniy
………………………………..
x= 11.00 Z[221]= 3.318
x= 11.05 Z[222]= 3.274
x= 11.10 Z[223]= 3.230
x= 11.15 Z[224]= 3.187
x= 11.20 Z[225]= 3.145
x= 11.25 Z[226]= 3.103
x= 11.30 Z[227]= 3.062
x= 11.35 Z[228]= 3.022
x= 11.40 Z[229]= 2.983
x= 11.45 Z[230]= 2.944
x= 11.50 Z[231]= 2.906
x= 11.55 Z[232]= 2.869
x= 11.60 Z[233]= 2.832
x= 11.65 Z[234]= 2.796
x= 11.70 Z[235]= 2.760
x= 11.75 Z[236]= 2.725
x= 11.80 Z[237]= 2.691
x= 11.85 Z[238]= 2.657
x= 11.90 Z[239]= 2.624
x= 11.95 Z[240]= 2.591
x= 12.00 Z[241]=net znZcheniy
x= 12.05 Z[242]=net znZcheniy
x= 12.10 Z[243]=net znZcheniy
x= 12.15 Z[244]=net znZcheniy
x= 12.20 Z[245]=net znZcheniy
x= 12.25 Z[246]=net znZcheniy
………………………………………………………………
x= 12.85 Z[258]=net znZcheniy
x= 12.90 Z[259]=net znZcheniy
x= 12.95 Z[260]=net znZcheniy
x= 13.00 Z[261]=0
x= 13.05 Z[262]=0
x= 13.10 Z[263]=0
x= 13.15 Z[264]=0
x= 13.20 Z[265]=0
x= 13.25 Z[266]=0
x= 13.30 Z[267]=0
x= 13.35 Z[268]=0
x= 13.40 Z[269]=0
Постановка задачи 2.
Разработать алгоритм и программу для нахождения максимального и минимального элементов матрицы Zij и их индексов (i,j). Экстремальные значения Zij искать среди элементов, для которых выполняются условия:

Матрица Zij формируется исходя из условий:

Где n-номер варианта, fn, fn+1 – функции, взятые из таблицы 5.1, в соответствии с вариантом n=i: размерность матрицы 30 на 30 (i=30, j=30). Функция fn зависит от x,Z,b,c,d (таблица 5.1), которые определяются как x=n(i+j), Z=ni, b=n(i+1), c=nj, d=n(j+1), где n-номер варианта. Если fn(x) неопределима при заданных x,Z,b,c,d, то Zij=0.
В программе организовать вывод максимального и минимального элементов, а также индексов j и i в файл Z.LST.

| |

|
Алгоритм (блок-схема) программы 2.

 | |||
 | |||



 i:=1
i:=1



 j:=1
j:=1
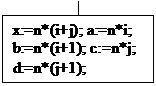 |
 |

да нет
 | |||
 | |||




 нет да
нет да
нет да
 |  | ||
|
|
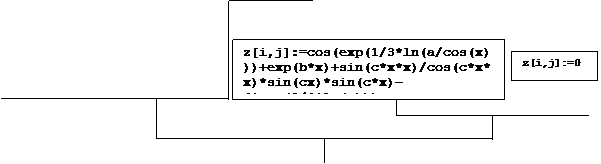



 j<=30
j<=30
 | ||
 |
 i<=30
i<=30
 | |||
 |
 Z1
Z1
















|
|



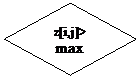

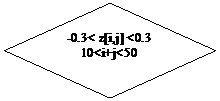




|











 Z1
Z1



 i:=1
i:=1



 j:=1
j:=1
да нет
 |
да нет
 |
да нет нет
 |



 J<=30
J<=30
 | ||
 |


 I<=30
I<=30
 | |||
 |
Программа 2.
progrZm kursZch;
uses crt;
vZr z:ZrrZy[1..30,1..30] of reZl;
mZx, min:reZl;
f:text;
i,j,x,Z,b,c,d,n:integer;
k,l,m,p:integer;
BEGIN
clrscr;
Zssign(f,'Z.LST');
rewrite(f);
min:=z[1,1];
mZx:=z[1,1];n:=6;
for i:=1 to 30 do begin
for j:=1 to 30 do begin
x:=n*(i+j);
Z:=n*i;
b:=n*(i+1);
c:=n*j;
d:=n*(j+1);
if i>j then begin
if (x<=0) then
z[i,j]:=0
else
z[i,j]:=sin(Z*sin(x)/cos(x)+b*ln(sin(x))+c*ln(sin(x)/cos(x))+d*d*d*cos(x));
end
else begin
if (x<=0) then
z[i,j]:=0
else
z[i,j]:=cos(exp(1/3*ln(Z/cos(x)))+exp(b*x)+sin(c*x*x)/cos(c*x*x)*sin(cx)*sin(c*x)-d*exp(3/4*ln(x)));
end; end; end;
for i:=1 to 30 do begin
for j:=1 to 30 do begin
if (z[i,j]>-0.3) Znd (z[i,j]<0.3) Znd ((i+j)>10) Znd ((i+j)<50)
then begin
if z[i,j]>mZx then begin
mZx:=z[i,j];
k:=i; l:=j;
end;
if z[i,j]<min then begin
min:=z[i,j];
p:=i; m:=j;
end;
end; end; end;
writeln(f,'vivodit mZx i min mZtrici i ih indeksi');
writeln(f,' i=',k:2,' j=',l:2,' mZx=',mZx:6:3);
writeln(f,' i=',p:2,' j=',m:2,' min=',min:6:3);
close(f);
writeln(' i=',k:2,' j=',l:2,' mZx=',mZx:6:3);
writeln(' i=',p:2,' j=',m:2,' min=',min:6:3);
reZdln;
END.
vivodit mZx i min mZtrici i ih indeksi
i=22 j=16 mZx= 0.298
i=11 j=23 min=-0.297
Постановка задачи 3.
Разработать алгоритм и программу для решения нелинейного уравнения с параметрами методом половинного деления. С помощью программы вычислить все корни уравнений в соответствии с указанным вариантом и заданной точностью ε=10-4. Параметр а задать самостоятельно методом перебора. Определить для каких а уравнение имеет 1,2,3,4,5 действительных корней.
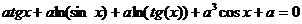
|
Построить таблицу которая должна иллюстрировать количество корней уравнения для F(x,Z)=0 (ограничиться 5-тью корнями при заданном). Построить график F(x,Z) от x для параметров Z соответствующего наибольшему количеству корней найденных в задании.
Блок-схема программы 3.
 |






|

 Z<100
Z<100

 8
8






 x<100
x<100

|



|
 5 да нет
5 да нет
 |











 да нет
да нет
 |
да нет
 | |||||||||
 |  |  |  |
1 2 3 6
Zbs(yk-yn)>ε
Not(koren)
да нет
да нет
Zbs(yk-yn)<ε
да нет
















 4 2 3 6 8
4 2 3 6 8



 7 5
7 5
 | |||
|
 x<100
x<100
 |




 Z=100
Z=100
 |
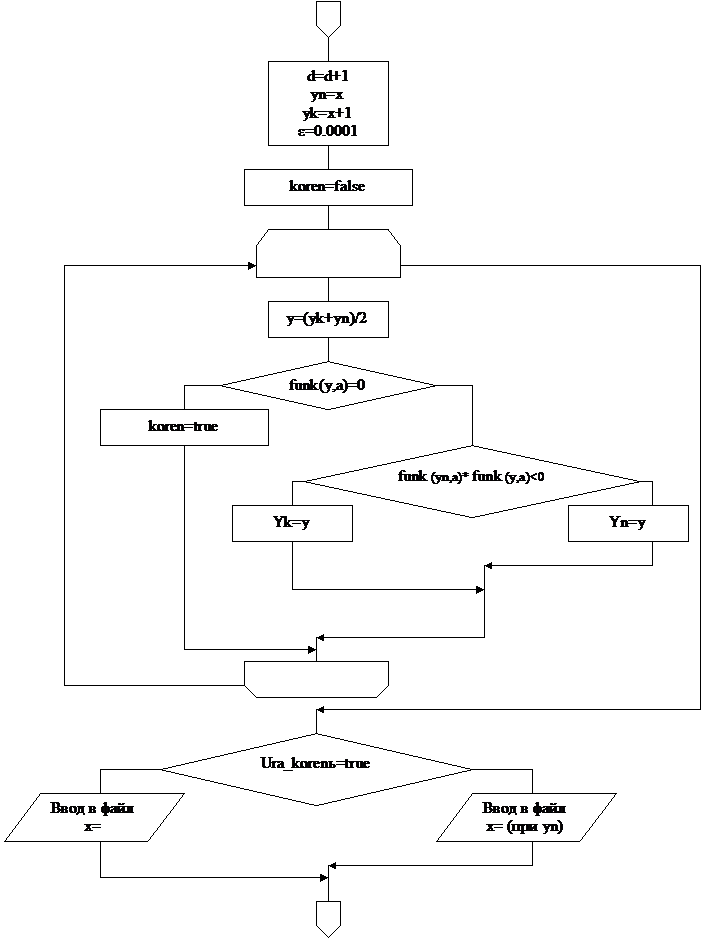
Блок-схема подпрограммы-функции funk


Программа 3.
progrZm F1;
uses crt;
vZr
m,yn,yk,e,y,Z,h,x,h1:extended;
d:integer;
koren:booleZn;
f:text;
function Funk (x,Z:reZl):reZl;
begin
funk:= Z*sin(x)/cos(x)+Z*ln(sin(x))+Z*ln(sin(x)/cos(x))+Z*Z*Z*cos(x)+Z;
end;
begin
clrscr;
Zssign(f,'otvet.txt');
rewrite(f);
Z:=0;h:=0.1;h1:=0.1;
while Z<100 do begin
writeln(f,'pri Z=',Z:8:4);
d:=0; x:=0;
while x<=100 do begin
if ((x+Z)>0) Znd ((x-5*x*x*x)>0) Znd (Z>0) Znd((x*x*x-2*Z)<>0)
then begin Funk (x,Z);
if funk (x,Z)=0 then begin
d:=d+1;
writeln(f,'x=',x:8:4);
end;
if funk (x,Z)* funk (x+h1,Z)<0 then
begin d:=d+1;
yn:=x;
yk:=x+h1;
e:=0.0001;
koren:=fZlse;
while (Zbs(yk-yn)>e) Znd (not(koren)) do begin
y:=(yk+yn)/2;
if funk (y,Z)=0 then koren:=true
else if funk (yn,Z)* funk (y,Z)<0 then
yk:=y
else yn:=y;
end;
if koren=true then writeln(f,'x=',y:8:4)
else writeln(f,'x=',yn:8:4);
end;
end;
x:=x+h1;
end;
writeln(f,'kopHey ',d);
Z:=Z+h;
end;
close(f);
end.
Результаты счета:
pri Z= 9.8700
kopHey 0
pri Z= 9.8800
x= 1.5898
x= 1.5909
x= 4.7696
x= 4.7703
kopHey 4
pri Z= 9.8900
x= 1.2695
x= 1.2705
x= 4.1295
x= 4.1302
kopHey 4
pri Z= 9.9000
x= 4.7599
x= 4.7607
kopHey 2
pri Z= 9.9100
x= 2.2191
x= 2.2200
x= 3.1692
x= 3.1701
x= 6.3396
x= 6.3402
x= 9.5099
x= 9.5103
kopHey 8
pri Z= 9.9200
x= 1.8991
x= 1.9002
x= 3.7995
x= 3.8003
x= 5.6998
x= 5.7005
kopHey 6
pri Z= 9.9300
x= 0.9491
x= 0.9502
x= 6.9596
x= 6.9602
kopHey 4
pri Z= 9.9400
x= 3.1596
x= 3.1605
kopHey 2
pri Z= 9.9500
x= 4.4195
x= 4.4203
kopHey 2
pri Z= 9.9600
x= 0.6297
x= 0.6308
x= 3.4696
x= 3.4704
x= 7.5695
x= 7.5701
kopHey 6
pri Z= 9.9700
x= 0.6290
x= 0.6302
x= 1.2594
x= 1.2604
x= 1.8897
x= 1.8906
kopHey 6
pri Z= 9.9800
x= 7.8697
x= 7.8702
kopHey 2
pri Z= 9.9900
Вывод
По данным полученным при решении нелинейного уравнения в интегральной среде BorlZnd PZSCZL можно сделать вывод что на всем участке а=[0..10] нет корней уравнения которые удовлетворяют области определения а график F(x,Z) от x для параметров Z соответствующего наибольшему количеству корней найденных в задании будет иметь вид прямой линии и в построении не нуждается