57. Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
58. 
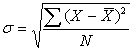
59. Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
60. 
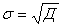
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее: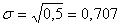 
.
Квадратический коэффициент вариации
61. Квадратический коэффициент вариации - это самый популярный относительный показатель вариации:
62. 
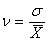
63. Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 - вариация считает слабой, а если больше 0,333 - сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина - нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫДЛЯ ИЗУЧЕНИЯ КУРСА
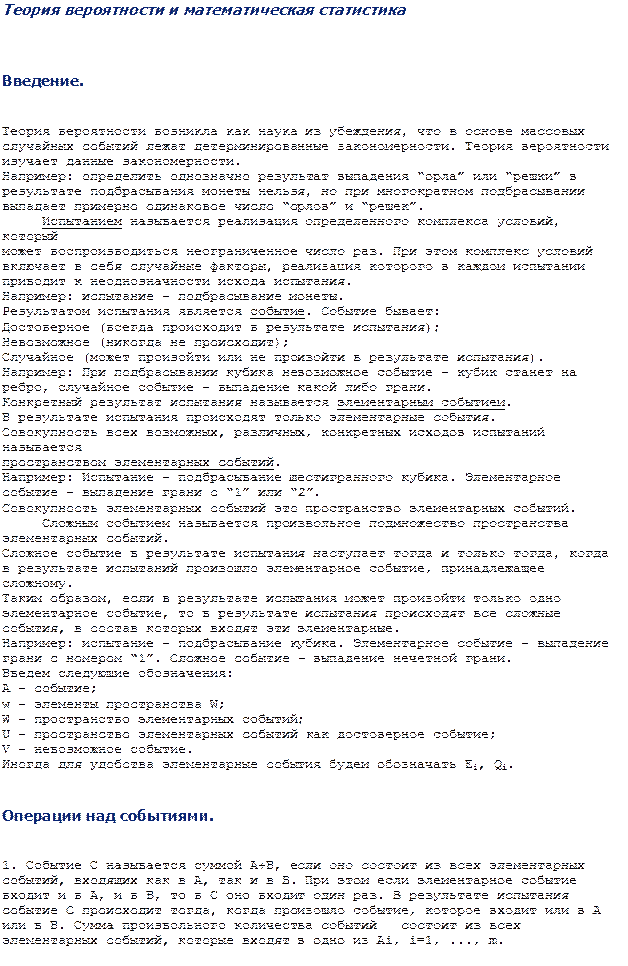2. Событие C произведением A и B, если оно состоит из всех элементарных
событий, входящих и в A, и в B. Произведением произвольного числа событий
называется событие состоящее из элементарных событий, входящих во все Ai,
i=1,..., m.
3. Разностью событий A-B называется событие C, состоящее из всех элементарных
событий, входящих в A, но не входящих в B.
4. Событие называется противоположным событию A, если оно удовлетворяет
|
|
двум свойствам.
Формулы де Моргана: 
и 
|
5. События A и B называются несовместными, если они никогда не могут
произойти в результате одного испытания.
События A и B называются несовместными, если они не имеют общих
элементарных событий.
C=A×B=V
Тут V - пустое множество.
Частость наступления события.
Пусть пространство элементарных событий конечно и состоит из m элементарных
событий. В этом случае в качестве возможных исходов испытаний рассматривают 2
m событий - множество всех подмножеств пространства элементарных событий W
и невозможное событие V.
Пример:
W=(w1, w2, w3)
A1=V
A2=(w1)
A3=(w2)
A4=(w3)
A5=(w1, w2)
A6=(w2, w3)
A7=(w1, w3)
A8=(w1, w2, w3)
Обозначим систему этих событий через F. Берем произвольное событие AÎF.
Проводим серию испытаний в количестве n. n - это количество испытаний, в
каждом из которых произошло событие A.
Частостью наступления события A в n испытаниях называется число 
Свойства частости
1. 
2. Частость достоверного события равна 1. Wn(U)=1.
3. Частость суммы попарно несовместных событий равна сумме частостей.
Рассмотрим систему Ai, i=1,..., k; события попарно несовместны, т.е.
Событие 
Пусть в результате некоторого испытания произошло событие A. По определению сумы
это означает, что в этом испытании произошло некоторое событие Ai.
Так как все события попарно несовместны, то это означает, что никакое другое
событие Aj (i¹j) в этом испытании произойти не может.
Следовательно:
nA=nA1+nA2+...+nA 
Теория вероятности используется при описании только таких испытаний, для которых
|
|
выполняется следующее предположение: Для любого события A частость наступления
этого события в любой бесконечной серии испытаний имеет один и тот же предел,
который называется вероятностью наступления события A.
Следовательно, если рассматривается вероятность наступления произвольного
события, то мы понимаем это число следующим образом: это частость наступления
события в бесконечной (достаточно длинной) серии испытаний.
К сожалению, попытка определить вероятность как предел частости, при числе
испытаний, стремящихся к бесконечности, закончилась неудачно. Хотя
американский ученый Мизес создал теорию вероятности, базирующуюся на этом
определении, но ее не признали из-за большого количества внутренних
логических несоответствий.
Теория вероятности как наука была построена на аксиоматике Колмогорова.