Построение вероятностного пространства.
Последовательно строим вероятностное пространство.
Этап 1:
Имеется испытание. В результате проведения испытания может наблюдаться одно
событие из серии событий e. Все события из системы e называются наблюдаемыми.
Введем предположение, что если события A Ì e, B Ì e наблюдаемы,
то наблюдаемы и события 
.
Система событий F называется полем событий или алгеброй событий, если для
двух произвольных событий A, B Ì F выполняется:
1) Дополнения 
2) (A+B) Î F, (A×B) Î F
3) все конечные суммы элементов из алгебры принадлежат алгебре
4) все конечные произведения элементов из алгебры принадлежат алгебре
5) все дополнения конечных сумм и произведений принадлежат алгебре.
Таким образом, систему e мы расширяем до алгебры или поля F путем включения
всех конечных сумм, произведений, и их дополнений. Т.е. считаем, что в
результате проведения испытания наблюдаемая система является полем или
алгеброй.
Множество всех подмножеств конечного числа событий является наблюдаемой
системой - алгеброй, полем.
Этап 2:
Каждому событию A Î F ставим в соответствие число P(A), которое называется
вероятностью наступления события A. Такая операция задает вероятностную
меру.
Вероятностная мера - числовая скалярная функция, аргументами которой
являются элементы из системы алгебры F. Введенная вероятностная мера
удовлетворяет системе из трех аксиом.
1. 

2. P(U)=1.
3. Рассмотрим конечную или бесконечную систему попарно несовместных
событий, каждое из которых принадлежит алгебре F.
 . Если
. Если  , то
, то  .
.
Алгебра событий называется s - алгеброй, если эта система событий содержит в
себе все конечные суммы и произведения из алгебры F и их дополнения, а также
все бесконечные суммы и произведения из алгебры и их дополнения.
Пример: В пространстве R1 зададим в качестве поля событий все
конечные интервалы вида a³x>b, b¹a.
Распространение этой алгебры на s - алгебру приводит к понятию борелевской
алгебры, элементы которой называются борелевскими множествами. Борелевская
алгебра получается не только расширением поля вида a³x>b, но и
расширением полей вида a>x³b, a³x³b.
Над наблюдаемым полем событий F задается счетно-аддитивная мера -
числовая скалярная функция, элементами которой являются элементы поля F, т.е.
события. Она удовлетворяет следующим трем условиям-аксиомам теории вероятности.
1. 

. P(A) - число, принадлежащее сегменту [0, 1] и называющееся вероятностью
наступления события A.
2. P(A) Î [0, 1] P(U)=1.
3. Пусть имеется A1, A2, A3,..., Ak - система попарно несовместных событий
 Если
Если  , то
, то  .
.
Лекция 1.
Предмет теории вероятностей. Случайные события. Алгебра событий. Относитель-ная частота и вероятность случайного события. Полная группа событий. Классичес-кое определение вероятности. Основные свойства вероятности. Основные формулы комбинаторики.
В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра — но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.
Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие — событие, которое всегда происходит при проведении опыта;
б) невозможное событие — событие, которое в результате опыта произойти не может;
в) случайное событие — событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным — выпадение 10 очков, а случайным — выпадение 3 очков.
Алгебра событий.
Определение 1.1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.
Пример 1. Два стрелка делают по одному выстрелу по мишени. Если событие А — попадание первого стрелка, а событие В — второго, то сумма А+В — это хотя бы одно попадание при двух выстрелах.
Пример 2. Если при броске игральной кости событием А i назвать выпадение i очков, то выпадение нечетного числа очков является суммой событий А1+А2+А3.
Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В (рис. 1).
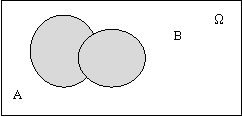
А В А + В
Рис.1.
Определение 1.2. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.

Пример 3. В примере 1 (два выстрела по мишени) событием АВ будет попадание обоих стрелков.
Пример 4. Если событие А состоит в том, что из колоды карт извлечена карта пиковой масти, а событие В — в том, что из колоды вынута дама, то событием АВ будет извлечение из колоды дамы пик.
Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В.
А В АВ

Рис.2.
Определение 1.3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В — нет.
Пример 5. Вернемся к примеру 1, где А\ В — попадание первого стрелка при промахе второго.
Пример 6. В примере 4 А\В — извлечение из колоды любой карты пиковой масти, кроме дамы. Наоборот, В \А — извлечение дамы любой масти, кроме пик.
А В А - В
Рис.3.
Введем еще несколько категорий событий.
Определение 1.4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.
Примеры: совместными событиями являются попадания двух стрелков в примере 1 и появление карты пиковой масти и дамы в примере 4; несовместными — события А1 — А6 в примере 2.
Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.
Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием.
Определение 1.5. Говорят, что события А1, А2,…,А п образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.
Замечание. В частности, если события, образующие полную группу, попарно несовмест-ны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.
Пример. В примере 2 события А1 — А6 (выпадение одного, двух,…, шести очков при одном броске игральной кости) образуют полную группу несовместных событий.
Определение 1.6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.
Примеры: выпадение любого числа очков при броске игральной кости, появление любой карты при случайном извлечении из колоды, выпадение герба или цифры при броске монеты и т.п.