Разберём весьма частный, однако, часто встречающийся случай: W состоит из конечного числа N равновероятных событий.
Понятие ''равновероятности'' здесь является исходным, неопределяемым. Основанием для суждения о равновозможности, равновероятности обычно служит физическая симметрия, равноправие исходов. Понятие "вероятность" здесь уже является производным, определяемым: вероятностью P (A) события A называется
P (A)= 
,
где N (A) – число элементарных событий, благоприятствующих событию A.
В этих условиях выведем основные формулы исчисления вероятностей.
1°. Вероятность достоверного события равна 1: P (W)=1. Это очевидно, так как N (W)= N.
2°. Вероятность невозможного события равна 0: P (Æ)=0. Это ясно, поскольку N (Æ)=0.
3°. P (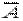
)=1- P (A). Справедливость равенства следует из равенства N (A)+
+ N (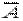)= N.
4°. 0£ P (A)£1 для " A, поскольку 0£ N (A)£ N.
5°. A Í B Û P (A)£ P (B), поскольку в этом случае N (A)£ N (B).
6°. Для любых событий A и B: P (AB)£ P (A), так как N (AB)£ N (A).
7°. Теорема сложения для несовместимых событий. Если события A и B несовместимы, то вероятность их суммы равна сумме вероятностей:
P (A + B)= P (A)+ P (B).
Действительно, N (A + B)= N (A)+ N (B) и остаётся разделить это равенство на N.
8°. Теорема сложения в общем случае:
P (A + B)= P (A)+ P (B)- P (AB).
Действительно, из определения суммы событий: N (A + B)= N (A)+ N (B)-
- N (AB). Деля почленно это равенство на N, убеждаемся в справедливости теоремы.
9°. Обобщение теоремы сложения на n событий:
P (A 1+ A 2+¼+ An)= 
(-1) k +1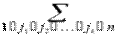 
P (Aj 1 Aj 2¼ Ajk).
Формула доказывается методом математической индукции несложно, но громоздко. Во внутренней сумме число слагаемых, очевидно, равно 
и суммирование ведётся по всевозможным наборам различных натуральных индексов j 1, j 2, ¼, jk.
|
|
10°. Условная вероятность.
Добавим к комплексу условий, реализация которых интерпретируется как опыт, ещё одно условие: произошло событие ^ B; это возможно практически лишь в случае, когда P (B)>0. Все опыты, в которых B не произошло, мы как бы игнорируем. Считаем, что добавление события B к комплексу условий не нарушает равновероятности исходов и не меняет природы самих исходов. Теперь опыт может иметь лишь один из N (B) исходов, а из них событию A благоприятствуют N (AB) исходов. В соответствии с классическим определением, вероятность события A при условии, что произошло событие B, равна:
P (A | B)= =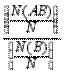 
= 
.
Таким образом, по существу, условная вероятность ничем не отличается от обычной, безусловной вероятности.
В случае, если A Í B, формула для условной вероятности упрощается:
P (A | B)= 
,
так как здесь AB = A.
11°. Теорема умножения: вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло:
P (AB)= P (B)× P (A | B)= P (A)× P (B | A).
Первая из этих формул для P (B)>0 является лишь формой записи формулы пункта 10° для условной вероятности; вторая получена из неё перестановкой местами A и B, что для P (A)>0 возможно. Вместе с тем ясно, что теорема умножения верна и для случая P (A)=0 или P (B)=0, но при этом она становится тривиальной и бессодержательной.
12°. Независимость событий.
Будем говорить, что событие ^ A не зависит от события B, если P (A | B)= P (A). В этом случае теорема умножения упрощается: P (AB)= P (A)× P (B).
|
|
И наоборот, для событий, имеющих положительную вероятность, из последней формулы следует независимость события A от B:
P (A | B)=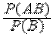 
= 
= P (A).
Таким образом, второе эквивалентное определение независимости: события A и B, имеющие положительные вероятности, независимы, если вероятность их произведения равна произведению их вероятностей: P (AB)= P (A) P (B). События A и B в этом определении симметричны: если событие A не зависит от B, то и B не зависит от A.
Если события A и B независимы, то независимы также и события A и 
.
Действительно:
P ( | A)+ P (B | A)= 
+ 
= 
= 
=1,
откуда:
P ( | A)=1- P (B | A)=1- P (B),
а это и доказывает наше утверждение.
Ясно, что независимы также и события , .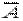
Если события A и B независимы, то они не могут быть несовместимыми: если A и B – одновременно несовместимы и независимы, то, с одной стороны, AB =Æ и P (AB)=0, а, с другой, – P (AB)= P (A)× P (B), что противоречит предположению о положительности вероятностей P (A) и P (B).
Обобщение понятия независимости на n событий: события A 1, A 2, ¼, An называются независимыми в совокупности, если для любого набора различных индексов j 1, j 2, ¼, jk вероятность произведения событий Aj 1 Aj 2¼ Ajk равна произведению вероятностей событий Aj 1, Aj 2, ¼, Ajk:
P (Aj 1 Aj 2¼ Ajk)= P (Aj 1)× P (Aj 2)×¼× P (Ajk).
Можно думать, что для независимости событий в совокупности достаточно попарной независимости, Конкретные примеры, однако, доказывают, что это не так.
Таким образом, для независимых событий легко вычислять вероятность произведения, а для несовместимых событий легко вычислять вероятность суммы.
|
|
Если события A 1, A 2, ¼, An независимы, то
P (A 1+ A 2+¼+ An)= P (
)=1- P (
)× P (
)×¼× P (
).
Если события A 1, A 2, ¼, An несовместимы, то
P ( × ×¼× )= P (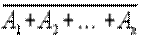
)=1- P (A 1+ A 2+¼+ An)=1- 
P (Ak).
13°. Теорема умножения для n событий:
P (A 1 A 2¼ An)= P (A 1)× P (A 2¼ An | A 1).
Учитывая, что условные вероятности ничем не отличаются от безусловных – лишь добавляется к комплексу условий ещё одно, которое в дальнейшем терять или отбрасывать нельзя, – можем продолжить:
P (A 1 A 2¼ An)= P (A 1)× P (A 2| A 1)× P (A 3¼ An | A 1 A 2) ¼.
Окончательно:
P (A 1 A 2¼ An)= P (A 1)× P (A 2| A 1)× P (A 3| A 1 A 2)×¼× P (An | A 1 A 2¼ An -1).
Эта теорема позволяет дать ещё одно определение независимости в совокупности: события A 1, A 2, ¼, An, имеющие положительные вероятности, независимы в совокупности, если для любого набора неравных индексов
P (Aj 1 Aj 2¼ Ajk | Ai 1 Ai 2¼ Aim)= P (Aj 1 Aj 2¼ Ajk),
что легко устанавливается по теореме умножения и формуле для условных вероятностей.
14°. Формула полной вероятности.
Пусть A 1, A 2, ¼, An – любое разбиение пространства W, B – любое событие. Тогда B = B W= B (A 1+ A 2+¼+ An)= BA 1+ BA 2+¼+ BAn и получаем формулу полной вероятности:
P (B)= 
P (BAk)= P (Ak)× P (B | Ak).
Обычно A 1, A 2, ¼, An – взаимоисключающие друг друга ситуации, в которых может происходить событие B.
15°. Формулы Байеса.
В обозначениях предыдущего пункта:
P (Ak | B)= 
= 
, k =1, 2, ¼, n,
и мы получили формулы Байеса, которые называют также формулами вероятностей гипотез: если событие B может произойти лишь с одним и только одним из событий A 1, A 2, ¼, An и оно действительно произошло, то, спрашивается, с каким из событий Ak оно произошло? Можно сделать n гипотез и, соответственно, формулы Байеса дают апостериорные вероятности P (Ak | B) для этих гипотез, выражая их через априорные вероятности P (Am) и условные вероятности P (B | Am) того, что в условиях m -ой гипотезы произойдёт событие B.
Таковы основные формулы исчисления вероятностей. Они получены в условиях весьма частного случая – классической схемы, т. е. для пространства конечного числа N равновероятных элементарных событий. В этой схеме число событий, которым благоприятствуют ровно k исходов, равно 
, а общее число различных событий, следовательно, равно 2 N.
Весьма неожиданно, что все полученные формулы являются общими и в действительности сохраняют свою силу для любого пространства элементарных событий. Покажем это.
^ Понятие об аксиоматическом построении
теории вероятностей
Пусть дано пространство элементарных событий W. Множество Å событий A, B, C, ¼ назовём полем событий, если
а) WÎÅ;
б) A, B ÎÅ Þ A + B ÎÅ, AB 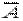ÎÅ, ÎÅ, ÎÅ.
Таким образом, введённые действия с событиями: сложение, умножение и переход к противоположному событию – не выводят нас из поля событий, поле событий замкнуто относительно этих операций.
Очевидно, также, что ÆÎÅ.
Примем следующие три аксиомы:
I. Любому событию A из поля событий Å приведено в соответствие неотрицательное число P (A), называемое вероятностью события A.
II. P (W)=1: вероятность достоверного события равна единице.
III. Аксиома сложения. Вероятность суммы несовместимых событий равна сумме их вероятностей.
Если A 1, A 2, ¼, An – попарно несовместимые события, то
P (A 1+ A 2+¼+ An)= P (Ak).
Тройка (W, Å, P (×)) называется вероятностным пространством.
Таким образом, поле событий Å является областью определения вероятностной функции P (×), при этом, как будет показано ниже (4°), отрезок [0; 1] является областью её значений.
Все пятнадцать формул исчисления вероятностей оказываются следствием трёх только что введённых аксиом. Действительно:
1°. P (W)=1 по II аксиоме.
2°. W+Æ=W, WÆ=Æ, поэтому по III аксиоме: P (W)+ P (Æ)= P (W), откуда P (Æ)=0.
В классической схеме были справедливы и обратные утверждения: если P (A)=1, то событие A – достоверное; если P (A)=0, то событие A – невозможное. В общей же схеме обратные утверждения, вообще говоря, ошибочны. Приходится вводить особые названия для событий единичной и нулевой вероятности: если P (A)=1, то говорят, что событие A происходит почти наверное, если P (A)=0, говорят, что событие A почти наверное не происходит. Пожалуй, именно это различие значительно усложняет строгую теорию вероятностей по сравнению с классическим случаем.
3°. A + 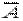=W и A 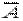=Æ. Поэтому по аксиомам III и II: P (A)+ P (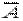)= P (W)=1. Отсюда: P (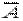)=1- P (A).
4°. По аксиоме I: P (A)³0. Так как P (A)+ P (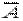)= P (W)=1, и, ввиду аксиомы I: P (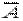)³0, то P (A)£1. Итак, для любого события A: 0£ P (A)£1.
5°. Если A Ì B, то B = A + 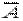B, и слагаемые здесь несовместимы. По аксиоме III: P (B)= P (A)+ P ( 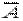B); по I аксиоме: P ( 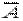B)³0; поэтому P (B)³ P (A).
6°. Для любых двух событий A и B: P (AB)£ P (A).
Действительно: A = AB + A и по аксиомам III и I:
P (A)= P (AB)+ P (A )³ P (AB).
7°. Формула P (A + B)= P (A)+ P (B) в случае, когда AB =Æ, верна по аксиоме III.
8°. Докажем теорему сложения для двух событий:
P (A + B)= P (A)+ P (B)- P (AB).
Очевидно,
A + B = A + B ,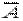
B = AB + B ,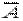
причём в обоих равенствах справа слагаемые несовместимы. По III аксиоме:
P (A + B)= P (A)+ P (B ),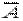
P (B)= P (AB)+ P (B ).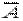
Вычитая почленно нижнее равенство из верхнего, получим теорему сложения.
9°. Теорема сложения для n событий
P (A 1+ A 2+¼+ An)= 
(-1) k +1 
P (Aj 1 Aj 2¼ Ajk)
является прямым следствием теоремы сложения для двух событий.
10°. Формула для условной вероятности
P (A | B)=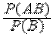
является определением условной вероятности в предположении, что вероятность P (^ B) ненулевая: P (B)>0. Вероятность P (A | B) показывает, какая часть вероятности P (B) приходится на долю события A.
11°. Прямым следствием определения условной вероятности оказывается формула:
P (AB)= P (B)× P (A | B)= P (A)× P (B | A).
12°. Совершенно так же, как и в классической схеме, на основе последних формул строится понятие независимости событий: события A и B независимы в том и только в том случае, когда P (AB)= P (A)× P (B).
13°. Теорема умножения для n событий
P (A 1 A 2¼ An)= P (A 1)× P (A 2| A 1)× P (A 3| A 1 A 2)×¼× P (An | A 1 A 2¼ An -1)
является прямым следствием теоремы умножения для двух событий.
14°, 15°. Выводы формулы полной вероятности и формул вероятностей гипотез воспроизводятся без изменений: для любого события B и любого разбиения пространства W (W= A 1+ A 2+¼+ An):
P (B)= P (Ak)× P (B | Ak),
P (Ak | B)= = , k =1, 2, ¼, n.
В более полных, чем наш, курсах теории вероятностей приходится рассматривать также и суммы бесконечного числа событий и, соответственно, требовать, чтобы эта операция не выводила из поля событий: для бесконечной последовательности попарно несовместимых событий A 1, A 2, ¼, An, ¼ требуют, чтобы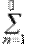 
An ÎÅ. Такие поля событий называются борелевскими полями или сигма-алгебрами. Приходится для борелевского поля событий усиливать аксиому III, распространяя её и на бесконечные суммы попарно несовместимых событий:
P (
An)= P (An).
Любопытно отметить, что в изложенном аксиоматическом построении теории вероятностей не нашлось места такому понятию, как событие "произошло" или "не произошло". Теория вероятностей оказывается частью теории меры, причём характерными свойствами вероятностной меры оказываются её неотрицательность: P (A)³0 и нормированность на единицу: P (W)=1. Просматривая выведенные свойства вероятностной функции P (×), можно заметить, что она ведёт себя подобно массе: единичная "масса вероятности" распределяется в пространстве W. Если нас интересует вероятность некоторого события A, то мы должны подсчитать, сколько этой массы досталось множеству A.
Одномерные случайные величины
Пусть имеется вероятностное пространство (W, Å, ^ P (×)) Определим на W числовую функцию X = X (w): каждому элементарному событию w приведено в соответствие вещественное число X (w).Такая функция называется случайной величиной. Мы ставим опыт, получаем элементарное событие w, смотрим, какое число X (w)= x было приведено ему в соответствие, и говорим: в опыте случайная величина X приняла значение x.
Рассмотрим простейший случай: число возможных значений случайной величины ^ X конечно или счётно:x 1, ¼, xk, ¼ Такую случайную величину называют дискретной. Законом распределения дискретной случайной величины называют совокупность вероятностей её возможных значений: pk = P { X = xk }. Будем предполагать, что события { X = xk } содержатся в поле событий Å, и тем самым вероятности pk определены.
Очевидно, одно и только одно из своих значений случайная величина обязательно примет. Поэтому выполняется равенство
pk =1,
называемое иногда условием нормировки в дискретном случае.
Задать случайную величину значит задать закон её распределения: т. е. указать её возможные значения и распределение вероятностей между ними.
^ В общем случае общепринятый способ задания случайной величины даёт так называемая функция распределения:
F (x)= P { X < x }.
Она указывает, какая вероятность досталась не отдельным точкам, а полуоси левее точки x, не включая саму точку x. Приходится дополнительно предполагать, что событие { X < x }ÎÅ, в противном случае функция распределения была бы не определена.
Дискретную случайную величину можно задавать её функцией распределения. Нетрудно сообразить, что это будет ступенчатая функция с разрывами в точках xk и скачками pk в этих точках:
F (x)= P { X < x }= 
P { X = xk }= 
pk,
где суммирование ведётся по всем тем возможным значениям X, которые оказались меньше x.
Если существует такая функция p (x), которая позволяет представить функцию распределения интегралом:
F (x)= 
p (x) dx,
то случайная величина X называется непрерывной, а p (x) – плотностью вероятности случайной величины X.
Функция распределения F (x) непрерывной случайной величины является непрерывной функцией (отсюда и название случайной величины), и, более того, – дифференцируемой функцией: F ¢(x)= p (x).
В более общем случае случайная величина X может принадлежать к смешанному типу: вероятность распределяется как между отдельными точками (дискретная составляющая), так и на интервалах (непрерывная составляющая). Если отдельным точкам xk достались вероятности pk, а остальная вероятность пошла на непрерывное распределение с линейной плотностью p (x), то:
F (x)= P { X < x }= 
P { X = xk }+ p (x) dx.
Если суммарная вероятность, доставшаяся точкам xk случайной величины X смешанного типа, равна A (pk = A), а на непрерывное распределение X уходит вероятность B, (
p (x) dx = B), то A + B =1.
Можно считать, что случайная величина X является смесью двух случайных величин: дискретной Y с возможными значениями xk и вероятностями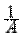 
pk и непрерывной Z с плотностью 
p (x). Функция распределения X имеет вид: F (x)= AFY (x)+ BFZ (x).
Вообще, если имеются случайные величины Xi, i =1, 2, ¼, n с функциямираспределения FXi (x), то смесью этих случайных величин называют случайную величину с функцией распределения
F (x)= 
AiFXi (x),
где числа Ai удовлетворяют условиям: 0£ Ai £1, A 1+ A 2+¼+ An =1, и играют роль весовых множителей, они регулируют вклад в смесь отдельных составляющих. Функция F (x), очевидно, обладает необходимыми свойствами функции распределения и может задавать случайную величину.
^ Основные свойства функции распределения F (x)
и плотности вероятности p (x)
1°. Считаем, что случайная величина X или совсем не принимает значений ±¥ или почти наверное их не принимает: P { X =+¥}= P { X =-¥}=0. При этом предположении:
F (x)= F (-¥)=0, 
F (x)= F (+¥)=1.
2°. F (x) – монотонно-неубывающая функция:
x 1< x 2 Þ F (x 1)£ F (x 2).
Действительно: { X < x 2}={ X < x 1}+{ x 1£ X < x 2}. Справа стоит сумма двух несовместимых событий. Поэтому:
P { X < x 2}= P { X < x 1}+ P { x 1£ X < x 2},
или:
F (x 2)= F (x 1)+ P { x 1£ X < x 2}
и неравенство F (x 2)³ F (x 1) следует из неотрицательности вероятности P { x 1£ X <
< x 2}.
3°. В доказательстве второго свойства мы выразили через функцию распределения вероятность попадания случайной величины ^ X в полуоткрытый интервал:
P { x 1£ X < x 2}= F (x 2)- F (x 1).
4°. Перепишем последнее равенство, взяв x 1= x, x 2= x +e, e>0:
P { x £ X < x +e}= F (x +e)- F (x).
Перейдём здесь к пределу при e®0: P { X = x }= 
F (x +e)- F (x)= F (x +0)- F (x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F (x +0)- F (x) её функции распределения в точке x. Во всех точках непрерывности F (x) этот скачок и, следовательно, вероятность P { X = x }, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности.
Если мы наблюдаем непрерывную случайную величину и получили значение X = x, то мы получили пример события A ={ X = x }, вероятность которого равна нулю, которое, однако, произошло, а событие 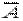={ X ¹ x }, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся.
Так как функция распределения определена равенством F (x)= P { X < x }, где под знаком вероятности стоит строгое неравенство, то вероятность, возможно сосредоточенная в точке x, не учитывается, поэтому F (x) – функция, непрерывная слева:
F (x -e)= F (x -0)= F (x).
5°. Теперь нетрудно выразить через F (x) вероятность попадания случайной величины в произвольный интервал:
P { x 1£ X £ x 2}= F (x 2+0)- F (x 1),
P { x 1< X < x 2}= F (x 2)- F (x 1+0),
P { x 1< X £ x 2}= F (x 2+0)- F (x 1+0).
6°. Плотность вероятности p (x) неотрицательна. Это следует из монотонного неубывания F (x).
7°. Переходя к пределу при x ®+¥ в равенстве F (x)= p (x) dx, и учитывая, что F (+¥)=1, получим условие нормировки для непрерывной случайной величины:
p (x) dx =1.
Геометрический смысл этого равенства: площадь под кривой плотности вероятности всегда равна единице.
8°. Общее правило вычисления вероятностей для дискретной и непрерывной случайной величины: если ^ A –– некоторое числовое множество на вещественной оси, то
P { X Î A }= P { X = xk },
P { X Î A }= 
p (x) dx
и ясно, что в непрерывном случае вероятность событий { X Î A } определена лишь для таких множеств A, для которых имеет смысл интеграл 
p (x) dx.
9°. Мы считаем, что задавая произвольную функцию F (x) с обязательными свойствами функции распределения: монотонное неубывание, непрерывность слева, F (-¥)=0, F (+¥)=1, – мы задаём некоторую случайную величину. Если F (x) – ступенчатая функция, то она задаёт дискретную случайную величину: точки скачков – её возможные значения, величины скачков – их вероятности.
Дискретную случайную величину можно задать таблицей её возможных значений и их вероятностей: xk, pk, k =1, 2, ¼, n, лишь бы были " pk ³0 и pk =1.
Непрерывную случайную величину можно задать плотностью вероятности p (x). В качестве таковой может служить любая неотрицательная функция, удовлетворяющая условию нормировки: p (x) dx =1.