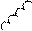
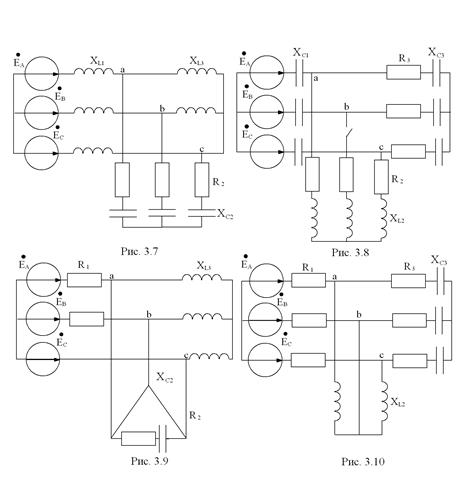
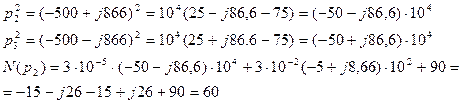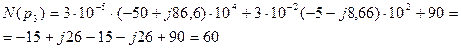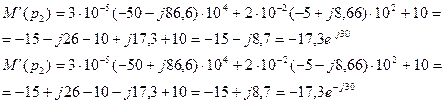К симметричному трехфазному генератору через сопротивления подключены два приемника, соединенные либо в звезду, либо в треугольник. Вследствие аварии произошло замыкание накоротко одного из сопротивлений или разрыв цепи (место разрыва на схемах указано соответствующим рубильником); электрическая цепь стала несимметричной.
Необходимо проделать следующее:
1. Определить токи во всех ветвях схемы методом двух узлов.
2. Построить в одной комплексной плоскости топографическую и векторную диаграммы токов.
3. Найти активную, реактивную и полную мощности трехфазной цепи.
4. Составить баланс активных мощностей.
На топографической диаграмме должны быть указаны векторы напряжения на всех элементах цепи.
Таблица 3.1
| № вар. | № рис. | ЕА, В | R1, Ом | R2, Ом | R3, Ом | XL1, Ом | XL2, Ом | XL3, Ом | XС1, Ом | XС2, Ом | XС3, Ом |
| 3.1 | |||||||||||
| 3.2 | |||||||||||
| 3.3 | |||||||||||
| 3.4 | |||||||||||
| 3.5 | |||||||||||
| 3.6 | |||||||||||
| 3.7 | |||||||||||
| 3.8 | |||||||||||
| 3.9 | |||||||||||
| 3.10 | |||||||||||
| 3.10 | |||||||||||
| 3.9 | |||||||||||
| 3.8 | |||||||||||
| 3.7 | |||||||||||
| 3.6 |
Окончание табл. 3.1
| № вар. | № рис. | ЕА, В | R1, Ом | R2, Ом | R3, Ом | XL1, Ом | XL2, Ом | XL3, Ом | XС1, Ом | XС2, Ом | XС3, Ом |
| 3.5 | |||||||||||
| 3.4 | |||||||||||
| 3.3 | |||||||||||
| 3.2 | |||||||||||
| 3.1 | |||||||||||
| 3.6 | |||||||||||
| 3.7 | |||||||||||
| 3.8 | |||||||||||
| 3.9 | |||||||||||
| 3.10 | |||||||||||
| 3.1 | |||||||||||
| 3.2 | |||||||||||
| 3.3 | |||||||||||
| 3.4 | |||||||||||
| 3.5 | |||||||||||
| 3.3 | |||||||||||
| 3.4 | |||||||||||
| 3.5 | |||||||||||
| 3.6 | |||||||||||
| 3.7 | |||||||||||
| 3.8 | |||||||||||
| 3.9 | |||||||||||
| 3.10 | |||||||||||
| 3.1 | |||||||||||
| 3.2 | |||||||||||
| 3.4 | |||||||||||
| 3.5 | |||||||||||
| 3.6 | |||||||||||
| 3.7 | |||||||||||
| 3.8 | |||||||||||
| 3.9 | |||||||||||
| 3.10 | |||||||||||
| 3.1 | |||||||||||
| 3.2 | |||||||||||
| 3.3 |














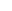


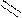

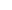 Пример
Пример
Определить токи в ветвях цепи методом двух узлов:
R1=R2=R3=15 Ом;
XL1=XL2=XL3=12 Ом;
XС1=XС2=XС3=20 Ом;
ЕА=270 В;

Рис. 3.11
Преобразуем звезду О’ в эквивалентный треугольник:

Аналогично – для YCbc и YCca:

|



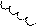




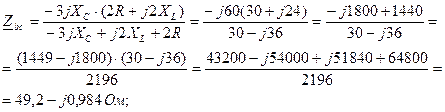


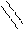 .
. 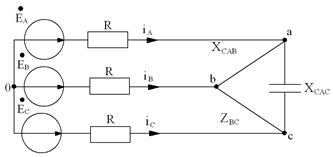
Рис. 3.13
Перейдем от треугольника к эквивалентной звезде:
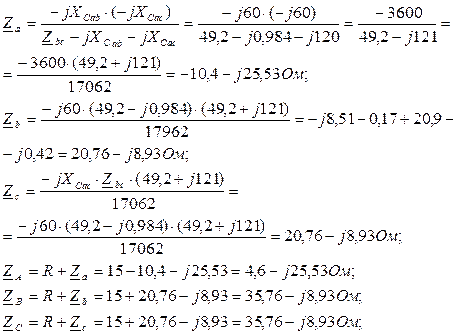
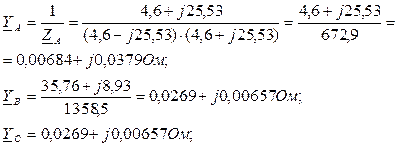
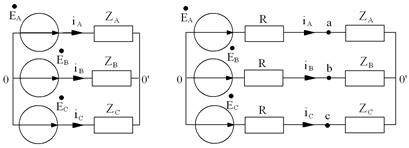
Рис. 3.14

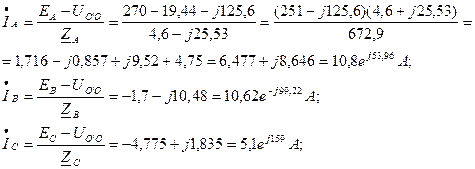 Определим напряжение
Определим напряжение 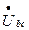 :
:
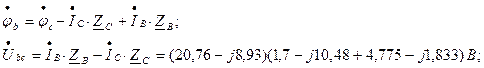
т.к. 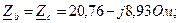
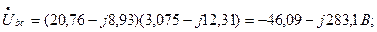
Определим ток 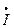 bO”OC:
bO”OC:
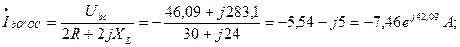
Определим токи 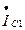 ;
; 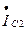 ;
; 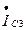 :
:
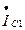 =
= 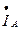 = 6,477+ j 8,646 =10,8 j 53,16 A;
= 6,477+ j 8,646 =10,8 j 53,16 A;
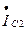 =
=  = - 1б7 -j 10б48 + 5б54 +j 5=3б84- j 5б48=6б69 e -j55 А;
= - 1б7 -j 10б48 + 5б54 +j 5=3б84- j 5б48=6б69 e -j55 А;
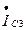 =
= 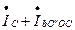 =- 4б775 +j 1б833 - 5б54 -j 5 =- 10б3 -j 3б17 =- 10б8 ej 17,09 A.
=- 4б775 +j 1б833 - 5б54 -j 5 =- 10б3 -j 3б17 =- 10б8 ej 17,09 A.
Определим полную, активную и реактивную мощности трехфазной цепи:

S=6934 B·A;
P=5501,7 Вт;
Q=4220,6 BAp.
Определим мощность на активных сопротивлениях цепи:
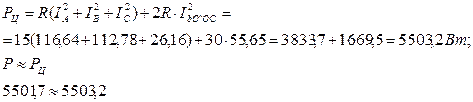
Переходные процессы в линейных
Электрических цепях
Расчётно-графическая работа № 4
Указания
Номер схемы соответствующий номеру варианта, активное сопротивление, индуктивность, ёмкость и начальная фаза синусоидально изменяющейся ЭДС заданы в табл. 4.1.
Задача
1. В заданной электрической цепи с источником постоянной ЭДС Е=100 В происходит коммутация.
Требуется: рассчитать ток на индуктивности операторным методом и ток через ёмкость классическим методом.
2. ЭДС источника напряжения изменяется с частотой w=1000 рад/с по синусоидальному закону. Амплитуда ЭДС равна Ем=100 В.
Коммутация происходит в момент времени t=0. До коммутации цепь работает в установившемся режиме.
Необходимо: определить классическим методом ток в одной из параллельных ветвей и операторным методом ток через источник.
Таблица 4.1
| № вар. | № рис. | R, Ом | L, Гн | С, Ф | Y, град |
| 4.1 | 5E-3 | (1/36)E-3 | |||
| 4.2 | 5E-3 | (5/2)E-2 | |||
| 4.3 | 2E-2 | (1/9)E-5 | |||
| 4.4 | 5E-3 | (1/2)E-4 | |||
| 4.5 | 1E-2 | 1E-4 | |||
| 4.6 | 2E-2 | (1/18)E-3 | |||
| 4.7 | 3E-2 | (5/4)E-5 | |||
| 4.8 | 4E-2 | 2E-5 | |||
| 4.9 | 1,5E-3 | 5E-5 | |||
| 4.10 | 5E-2 | (15/36)E-4 | |||
| 4.1 | 5E-2 | (15/36)E-4 | |||
| 4.2 | 1,5E-3 | 5E-5 | |||
| 4.3 | 4E-2 | 2E-5 | |||
| 4.4 | 3E-2 | (5/4)E-5 | |||
| 4.5 | 2E-2 | (1/18)E-5 | |||
| 4.6 | 1E-2 | 1E-4 | |||
| 4.7 | 5E-3 | (1/2)E-4 | |||
| 4.8 | 2E-2 | (1/9)E-5 | |||
| 4.9 | 5E-3 | (5/2)E-2 | |||
| 4.10 | 5E-3 | (1/36)E-3 | |||
| 4.1 | 1E-2 | 1E-4 | |||
| 4.2 | 5E-3 | (1/2)E-4 | |||
| 4.3 | 2E-2 | (1/9)E-3 | |||
| 4.4 | 5E-3 | (5/2)E-2 | |||
| 4.5 | 5E-3 | (1/36)E-3 | |||
| 4.6 | 2E-2 | (1/9)E-5 | |||
| 4.7 | 1E-3 | (1/2)E-4 |
Окончание табл.4.1
| № вар. | № рис. | R, Ом | L, Гн | С, Ф | Y, град |
| 4.8 | 5E-3 | 1E-4 | |||
| 4.9 | 3E-2 | (5/4)E-5 | |||
| 4.10 | 4E-2 | 2E-5 | |||
| 4.1 | 1,5E-2 | 5E-5 | |||
| 4.2 | 5E-2 | (15/36)E-4 | |||
| 4.3 | 5E-2 | (15/36)E-4 | |||
| 4.4 | 1,5E-3 | 5E-5 | |||
| 4.5 | 4E-2 | 2E-5 | |||
| 4.6 | 3E-2 | (5/4)E-5 | |||
| 4.7 | 2E-2 | (1/18)E-5 | |||
| 4.8 | 1E-2 | 1E-4 | |||
| 4.9 | 5E-3 | (1/2)E-4 | |||
| 4.10 | 2E-2 | (1/9)E-5 | |||
| 4.1 | 5E-3 | (5/2)E-2 | |||
| 4.2 | 5E-3 | (1/36)E-3 | |||
| 4.3 | 1E-2 | 1E-4 | |||
| 4.4 | 5E-3 | (1/2)E-4 | |||
| 4.5 | 2E-2 | (1/9)E-3 | |||
| 4.6 | 5E-3 | (5/2)E-2 | |||
| 4.7 | 5E-3 | (1/36)E-3 | |||
| 4.8 | 1E-3 | (3/2)E-2 | |||
| 4.9 | 15E-3 | 2E-2 | |||
| 4.10 | 8E-3 | 1E-3 |

Задача
В электрической цепи (рис. 4.1) R1=20 Ом, R=10 Ом, L=10 мГн, С=100 мкФ, U=90 В.
Определить ток в индуктивности при переходном процессе двумя методами: классическим и операторным.
Построить график iL(t).
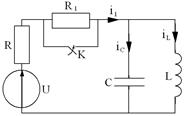
Рис. 4.1
1. Классический метод.
1.1. Определим независимые начальные условия
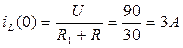
uc(0)=0, так как сопротивление индуктивности постоянному току равно нулю.
1.2. Определим величину принужденного тока для послекоммутационной цепи
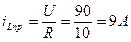
1.3. Составим и решим характеристическое уравнение
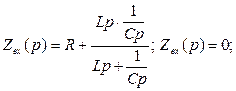
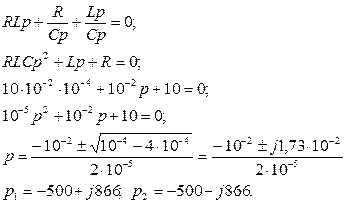
1.4. Корни характеристического уравнения комплексно сопряженные, следовательно функция свободного тока имеет вид:

Постоянными интегрирования в уравнении будут А и φ.
1.5. Составим систему уравнений для определения постоянных интегрирования
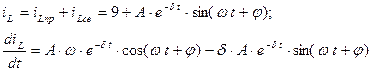
1.6. Независимые начальные условия
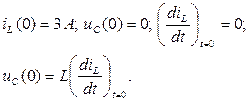
1.7. Решим систему (1.5.) для t=0

1.7. Искомая величина тока

2. Операторный метод.
2.1. Составим операторную схему цепи по известным независимым начальным условиям (рис. 4.2).
|
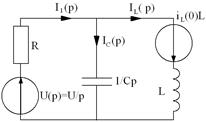
Рис. 4.2
2.2. Составим систему уравнений по законам Кирхгофа
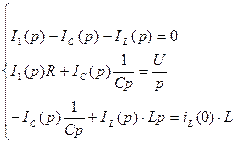



2.4. Перейдем от изображения к оригиналу по теореме разложения
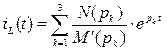
Корни