Пример выполнения расчетно-графической работы № 1

Анализ линейных электрических цепей

Постоянного тока

Расчётно-графическая работа № 1

Для электрической цепи с заданным графом (рис. 1.1-1.4), схемой ветвей (рис. 1.5) и заданными параметрами элементов схемы (табл. 1.1) провести следующий анализ.

1 Составить матрицу соединений [А].

2 Нарисовать одно из деревьев графа с указанием (штриховой линией) ветвей связи.

3 Выбрать главное сечение и составить матрицу сечений [Д].

4 Записать с помощью матриц [А] и [Д] две системы уравнений по первому закону Кирхгофа (для узлов и сечений).

5 Выбрать главные контуры и составить матрицу контуров [В].

6 Записать с помощью матрицы [В] систему уравнений по второму закону Кирхгофа.

7 Записать для каждой ветви компонентное уравнение ветви (используя обобщённый закон Ома).

8 Составить систему узловых уравнений, определить потенциалы, напряжения на ветвях и токи в ветвях.

9 Составить систему контурных уравнений, определить токи в ветвях.

Внимание! Уравнения по п.8 и 9 составить без эквивалентного преобразования электрической схемы.

10 Определить ток I₄ в четвёртой ветви методом эквивалентного генератора.

11 Проверить соблюдение баланса мощности в электрической цепи. Определить расход энергии за t=10 секунд.

12 Для любого контура с двумя источниками ЭДС построить потенциальную диаграмму.

 

Таблица 1.1

№ вар.	№ рис.	ПАРАМЕТРЫЭЛЕМЕНТОВ ЦЕПИ
Е1 В	Е2 В	Е3 В	Е4 В	Е5 В	Е6 В	I1 A	I2 A	I3 A	I4 A	I5 A	I6 A	R1 Oм	R2 Oм	R3 Oм	R4 Oм	R5 Oм	R6 Oм
	1.1														¥
	1.2														¥
	1.3														¥
	1.4														¥
	1.1													¥
	1.2													¥
	1.3													¥
	1.4													¥
	1.1							1,5						¥
	1.2							1,5						¥
	1.3							1,5						¥
	1.4							1,5						¥
	1.1									1,5						¥
	1.2									1,5						¥
	1.3									1,5						¥
	1.4									1,5						¥
	1.1														¥
	1.2														¥
	1.3														¥
	1.4														¥
	1.1													¥
	1.2													¥
	1.3													¥

Окончание табл. 1.1

	1.4													¥
	1.1							1,5						¥
	1.2							1,5						¥
	1.3							1,5						¥
	1.4							1,5						¥
	1.1									1,5						¥
	1.2									1,5						¥
	1.3									1,5						¥
	1.4									1,5						¥
	1.1														¥
	1.2														¥
	1.3														¥
	1.4														¥
	1.1													¥
	1.2													¥
	1.3													¥
	1.4													¥
	1.1							1,5						¥
	1.2							1,5						¥
	1.3							1,5						¥
	1.4							1,5						¥
	1.1															¥
	1.2															¥
	1.3															¥
	1.4															¥
	1.1														¥
	1.2														¥

	2 (2) 3

(1) (4)

(3)

3 5

(1) (3)

 

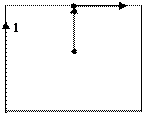Рис. 1.5

Пример выполнения расчетно-графической работы № 1

(1)

 

	(2)

 

1 4

 

Рис. 1.6

 

 

Рис. 1.7

 

R₂=3 Ом; R₄=5 Ом; R₆=2 Ом.

Е₁=2 В; Е₄=3 В; Е₆=3В.

J₃=1 А; J₅=2 А.

 

Рис. 1.8

Схема с положительными направлениями токов и напряжений, выбранными по направленному графу.

1. Составить матрицу соединений [A]:

2. Нарисовать одно из деревьев графа с указанием (штриховой линией) ветвей связи:

(1)

 

(3)

(2)

1 4

6

 

(4)

 

Рис. 1.9.

3. Выбрать главные сечения и составить матрицу сечений [ Д ]:

(1)

 

(2)

(3)

1 4

(4)

 

 

	Рис. 1.10

 

Номера сечений указаны в кружочках.

Матрица сечений [Д]= ;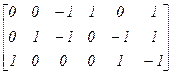

4. Записать с помощью матриц [А] и [Д] две системы уравнений по 2-му закону Кирхгофа:

а) для узлов [А] [I]=0:

 

б) для сечений: [Д] [I]=0

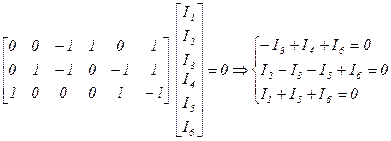
5. Выбрать главные контуры и составить матрицу контуров [B]:

(1)

 

(2)

(3)

1 I 4

II

6

 

Рис. 1.11

(4)

Матрица контуров

6. Записать с помощью матрицы [B] систему уравнений по 2-му закону Кирхгофа:

[B][U]=0;

 

7. Записать для каждой ветви компонентное уравнение (используя обобщенный закон Ома):

U2=I2R2 U2=φ1-φ2

U1=-E1 U1=φ1-φ2

U4=I4R4 U4=φ2-φ3

I3=J3 U3=φ2-φ1

U6=I6R6-E6 U6=φ6-φ3

UR5=I5-J5 U5=(I5-J5)R5 U5=φ2-φ4

8. Составить систему узловых уравнений, определить потенциалы, напряжения на ветвях и токи в ветвях:

XIlkHHrDwmA

Рис. 1.12

Для решения методом узловых потенциалов принимаем .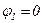

 

Система узловых уравнений: число уравнений N=N_y-N_B-1,

где: N_y=4 – число узлов,

N_B=1 – число вырожденных ветвей (ветви с 1-м источником ЭДС),

т.е. для данной цепи: N=4-1-1=2.

где , т.е.

 

 

 

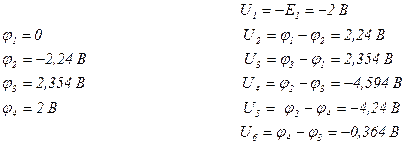
Токи в ветвях: I₃ = J₃ = 1 A

 

Проверка

 

 

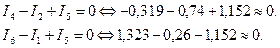
9. Составить систему контурных уравнений, определить токи в ветвях:

IR5

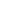
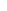
Рис. 1.13

 

На рисунке выбраны независимые контуры и их направление обхода (положительное направление контурных токов).

Число уравнений равно числу независимых контуров, ветвь с источником тока не может создать независимый контур.

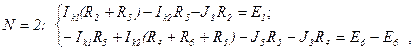
т.е. J₅ как контурный ток "замыкаем" через R₅, J_{3 ,} через R₂, E₄, R₄. В матричной форме

 

 

 

10. Определить ток I₄ в четвертой ветви эквивалентного генератора:

 

Рис. 1.14

 

 

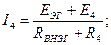
Е_ЭГ – определяем как U_23xx;

 

R_ВНЭГ – определяем как R_ВН23 при разомкнутой четвертой ветви.

Эквивалентная схема для определения R_ВНЭГ:

 

Рис. 1.15

Схема для определения E_ЭГ:

Рис. 1.16

пусть

11. Проверить соблюдение баланса мощности в электрической цепи. Определить расход энергии за t=10 с.

 

Мощность, расходуемая источниками:

 

Мощность, рассеиваемая резисторами:

 

Энергия, расходуемая за t=10 с. в электрической цепи: W=Pt=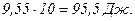

 

12. Для любого контура с двумя источниками ЭДС построить потенциальную диаграмму:

 

Потенциальная диаграмма, обход по контуру: E₁, E₆, R₆, R₄, R₂. показана на рис.1.17

		φ1

 

 

Е4

1 2 3 4 5 6 7 8 9 10 R, Ом

R2

R4

R6

-1

		φ2

 

 

Рис. 1.17