Уважаемые студенты, высылаю вам примеры решения задач по различным тема курса физики (1 семестр). Вам необходимо изучить и постараться разобраться в этих примерах. Это поможет вам успешно выполнить лабораторные работы. Лабораторные работы вы получите на занятии по расписанию. Там же будет подробная инструкция по выполнению и оформлению лабораторной работы.
ВНИМАНИЕ! Каждый студент после получения каждой лекции, практического задания или лабораторного задания должен отправить мне на почту сообщение следующего содержания:
Я Ф.И.О., студент группы …. (например20ПИзо,20ЭТзо, и т.д.) материал для изучения (физики) получил.
Это будет своего рода перекличкой, т.е. свидетельство вашего присутствия на сессии.
ЭЛЕКТРОСТАТИКА
ЗАКОН КУЛОНА. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ТЕЛ
Основные формулы
· Закон Кулона
,
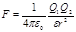где F — сила взаимодействия двухточечных зарядов Q1, и Q 2; r — расстояние между зарядами; e — диэлектрическая проницаемость среды; e 0 — электрическая постоянная:
.
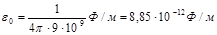Закон сохранения заряда
,
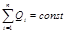где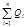 
— алгебраическаясумма зарядов,входящихв изолированную систему; n — число зарядов.
Примеры решения задач
Пример 1. Три одинаковых положительных заряда Q1 = Q2 = Q3 =1 нКл расположены по вершинам равностороннего треугольника (рис. 13.1). Какой отрицательный заряд Q4 нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?
Решение. Все три заряда, расположенных по вершинам треугольника, находятся в одинаковых условиях. Поэтому для решения задачи достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы один из трех зарядов, например Q1,
находился в равновесии.
В соответствии с принципом суперпозиции на заряд действует каждый заряд независимо от остальных. Поэтому заряд Q1 будетнаходиться в равновесии, если векторная сумма действующих на него сил равна нулю:
F 1 + F 3 + F 4 = F + F 4 =0, (1)
где F 2, F 3, F 4 — силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3 и Q4; F — равнодействующая сил F 2 и F 3.
Так как силы F и F 4 направлены по одной прямой, то векторное равенство (1) можно заменить скалярной суммой:
F—F4 =0, или F4 = F.
Выразив в последнем равенстве F через F2 и F3 и учитывая, что F3 = F2, получим
.
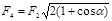Применяя закон Кулона и имея в виду, что Q2 = Q3 = Q1, найдем
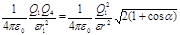, (2)
откуда
.
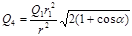Из геометрических построений в равностороннем треугольнике следует, что
.
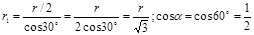С учетом этого формула (2) примет вид
.
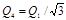Подставив сюда значение Q1, получим
Q4 =0,58 нКл.
Отметим, что равновесие системы зарядов будет неустойчивым.
Пример 2. Два заряда 9 Q и - Q закреплены на расстоянии l =50 см друг от друга. Третий заряд Q1 может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q1, при котором он будет находиться в равновесии. При каком знаке заряда равновесие будет устойчивым *?
Решение. Заряд Q1 будет находиться в равновесии в том случае, если векторная сумма сил, действующих на него, будет равна нулю. Это значит, что на заряд Q1 должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (рис. 13.2) может быть выполнено это условие. Для определенности будем считать, что заряд Q1 —положительный.
*Равновесие называется устойчивым, если при малом смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия.
На участке I (рис. 13.2, а) на заряд Q1 действуют две противоположно направленные силы: F 1 и F 2. Сила F 1, действующая со стороны заряда 9 Q, в любой точке этого участка будет больше, чем сила F 2, действующая со стороны заряда - Q, так как больший (по модулю) заряд 9 Q всегда находится ближе к заряду Q1, чем меньший заряд -Q. Поэтому равновесие на этом участке невозможно;
На участке II (рис. 13.2, б) обе силы F 1 и F 2 направлены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.
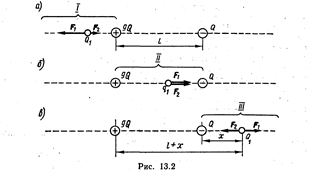
На участке III (рис. 13.2, б) силы F 1 и F 2 направление противоположные стороны, так же как и на участке I, но в отличие от него меньший (по модулю) заряд (— Q) всегда находится ближе к заряду Q1, чем больший заряд (9 Q). Это значит, что можно найти такую точку на прямой, где силы F 1 и F 2 будут одинаковы по модулю, т. е.
|F 1 |=|-F 2 |. (1)
Пусть расстояние от меньшего заряда до заряда Q1 равно х, тогда расстояние от большего заряда будет l+х. Выражая в равенстве (1) F1 и F2 в соответствии с законом Кулона, получим
.
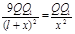Сокращая на QQ1 и извлекая из обеих частей равенства квадратный корень, найдем l + x =±3 x, откуда x1 =+ l /2 и x2=-l /4.
Корень x2 не удовлетворяет физическому условию задачи (в этой точке силы F1 и F2 хотя и равны по модулю, но направлены в одну сторону).
Определим знак заряда, при котором равновесие будет устойчивым. Рассмотрим смещение заряда Q1 в двух случаях: 1) заряд положителен;2) заряд отрицателен.
1. Если заряд Q1 положителен, то при смещении его влево обе силы F1 и F2 возрастают, но F1 возрастает медленнее (заряд 9 Q всегда находится дальше, чем – Q). Следовательно, F2 (по модулю) больше, чем F1, и на заряд Q1 будет действовать результирующая сила, направленная также влево. Под действием этой силы заряд Q1 удаляется от положения равновесия. То же происходит и при смещении заряда Q1 вправо. Сила F2 убывает быстрее, чем F1. Векторная сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
2. Если заряд Q1 отрицателен, то его смещение влево вызовет увеличение сил F2 и F1, но сила F1 возрастает медленнее, чем F2, т.е. | F2 |>| F1 |. Результирующая сила будет направлена вправо. Под действием этой силы заряд Q1 возвращается к положению равновесия. При смещении Q1 вправо сила F2 убывает быстрее, чем F1, т. е. | F1 |>| F2 |. результирующая сила направлена влево и заряд Q1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q1 несущественна.
Отметим, что в электростатике устойчивое равновесие возможно только при определенных ограничениях. В нашем примере заряд Q1 может перемещаться только вдоль прямой, проходящей через заряды Q и –9 Q. Если это ограничение снять, то устойчивого равновесия не будет. В системе зарядов, находящихся под действием одних только электростатических сил, устойчивое равновесие невозможно (теорема Ирншоу).
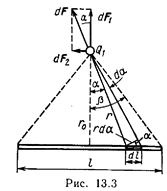Пример 3. Тонкий стержень длиной l =30 см (рис. 13.3) несет равномерно распределенный по длине заряд с линейной плотностью t=1 мкКл/м. На расстоянии r0 =20 см от стержня находится заряд Q1 =10 нКл, равноудаленный от концов, стержня. Определить силу F взаимодействия точечного заряда с заряженным стержнем.
Решение. Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределенный по длине стержня. Однако если выделить на стержне дифференциально малый участок длиной d l, то находящийся на нем заряд dQ =td l можно рассматривать как точечный и тогда по закону Кулона* сила взаимодействия между зарядами Q1 и d Q:
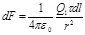, (1)
где r — расстояние от выделенного элемента до заряда Q1.
Из чертежа (рис. 13.3) следует, что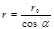 
и 
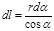, где
r0 — расстояние от заряда Q1 до стержня. Подставив эти выражения r к d l в формулу (1), получим
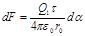. (2)
Следует иметь в виду, что d F — вектор, поэтому, преждечеминтегрировать разложим его на две составляющие: d F 1, перпендикулярную стержню, и d F 2, параллельную ему.
Из рис. 13.3 видно, что d F1 =d F cosa, d F 2=d F sina. Подставляя значение d F из выражения (2) в эти формулы, найдем:
.
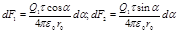* Здесь и далее, если в условии задачи не указана среда, имеется в виду, что заряды находятся в вакууме (e=1).
Интегрируя эти выражения в пределах от –b до +b, получим
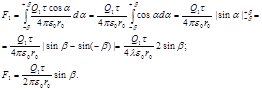
В силу симметрии расположения заряда Q1 относительно стержня интегрирования второго выражения дает нуль;
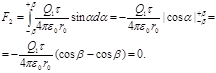
Таким образом, сила, действующая на заряд Q1,
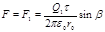. (3)
Из. рис. 13.3 следует, что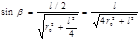 
. Подставив это выражение sinb в формулу (3), получим
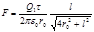. (4)
Произведем вычисления по формуле (4):
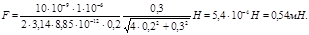
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
Основные формулы
· Напряженность электрического поля
E = F / Q,
где F — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.
· Сила, действующая на точечный заряд Q, помещенный в электрическое поле,
F = Q E.
· Поток вектора напряженности Е электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле,
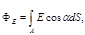или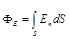 
,
где a — угол между вектором напряженности Е и нормалью n к элементу поверхности; d S — площадь элемента поверхности; En — проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле,
Ф E=ЕS cosa.
· Поток вектора напряженности Е через замкнутую поверхность
,
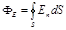где интегрирование ведется по всей поверхности.
· Теорема Остроградского — Гаусса. Поток вектора напряженности Е через любую замкнутую поверхность, охватывающую заряды Ql, Q2,..., Qn,
,
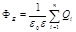где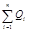 
— алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; п — число зарядов.
· Напряженность электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда,
.
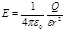Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд Q, на расстоянии r от центра сферы:
а) внутри сферы (r<.R)
E =0;
б) на поверхности сферы (r = R)
;
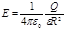в) вне сферы (r>R)
.
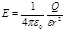· Принцип суперпозиции (наложения) электрических полей, согласно которому напряженность Е результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:
Е = E 1 + Е 2 +...+ Е n.
В случае двух электрических полей с напряженностями Е 1 и Е 2 модуль вектора напряженности
,
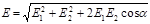где a — угол между векторами E 1 и E 2.
· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянии r от ее оси,
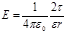, где t — линейная плотность заряда.
Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити (цилиндра):
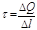
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,
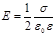
где s — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:
.
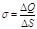· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью о заряда (поле плоского конденсатора)
.
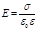Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Электрическое смещение D связано с напряженностью E электрического поля соотношением
D =e 0 e E.
Это соотношение справедливо только дляизотропных диэлектриков.
· Поток вектора электрического смещения выражается аналогично потоку вектора напряженности электрического поля:
а) в случае однородного поля поток сквозь плоскую поверхность
;
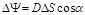б) в случае неоднородного поля и произвольной поверхности
,
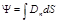где Dn — проекция вектора D на направление нормали к элементу поверхности, площадь которой равна d S.
· Теорема Остроградского — Гаусса. Поток вектора электрического смещения сквозь любую замкнутую поверхность, охватывающую заряды Q1, Q2,..., Qn,
,
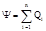где п —число зарядов (со своим знаком), заключенных внутри замкнутой поверхности.
· Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру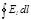 
, где El— проекция вектора напряженности Е в данной точке контура на направление касательной к контуру в той же точке.
В случае электростатического поля циркуляция вектора напряженности равна нулю:
.
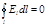Примеры решения задач
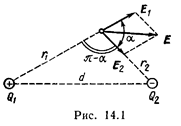
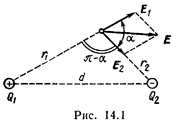Пример 1. Электрическое поле создано двумя точечными зарядами: Q1 =30 нКл и Q2 = –10 нКл. Расстояние d между зарядами равно 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r1 =15 см от первого и на расстоянии r2 =10 см от второго зарядов.
Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность Е электрического поля в искомой точке может быть найдена как векторная сумма напряженностей E 1 и Е 2 полей, создаваемых каждым зарядом в отдельности: E = E 1 + E 2.
Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны
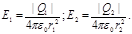(1)
Вектор E 1 (рис. 14.1) направлен по силовой линии от заряда Q1, так как заряд Q1 >0; вектор Е 2 направлен также по силовой линии, но к заряду Q2, так как Q2 <0.
Модуль вектора Е найдем по теореме косинусов:
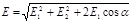, (2)
где угол a может быть найден из треугольника со сторонами r1, r2 и d:
.
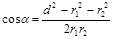В данном случае во избежание громоздких записей вычислим отдельно значение cosa. По этой формуле найдем
cosa =0,25.
Подставляя выражения E1 и E2 а по формулам (1) в равенство (2) и вынося общий множитель 1/(4pe 0) за знак корня, получаем
.
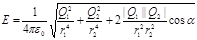Подставив значения величин p, e 0, Q1, Q2, r1 -, r2 и a в последнюю формулу и произведя вычисления, найдем
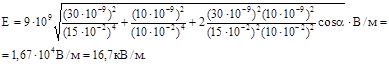
Пример 2. Электрическое поле создано двумя параллельными бесконечными заряженными плоскостями с поверхностными плотностями заряда s 1 =0,4 мкКл/м2 и s 2 =0,1 мкКл/м2. Определить напряженность электрического поля, созданного этими заряженными плоскостями.
Решение. Согласно принципу суперпозиции, поля, создаваемые каждой заряженной плоскостью в отдельности, накладываются друг на друга, причем каждая заряженная плоскость создает электрическое поле независимо от присутствия другой заряженной плоскости (рис. 14.2).
Напряженности однородных электрических полей, создаваемых первой и второй плоскостями, соответственно равны:
; 
.
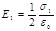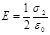Плоскости делят все пространство на три области: I, II и III. Как вид но из рисунка, в первой и третьей областях электрические силовые линии обоих полей направлены в одну сторону и, следовательно, напряженности суммарных полей Е(I) и E (III) в первой и третьей областях равны между собой и равны сумме напряженностей полей, создаваемых первой и второй плоскостями: Е(I)= E (III)= E1+E2, или
Е(I)= E (III) =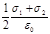 
.
Во второй области (между плоскостями) электрические силовые линии полей направлены в противоположные стороны и, следовательно, напряженность поля E(II) равна разности напряженностей полей, создаваемых первой и второй плоскостями: E(II)=|E1-E2|, или
.
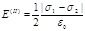Подставив данные и произведя вычисления, получим
E(I)=E(III)=28,3кВ/м=17 кВ/м.
Картина распределения силовых линий суммарного поля представлена на рис. 14.3.
Пример 3. На пластинах плоского воздушного конденсатора находится заряд Q =10 нКл. Площадь S каждой пластины конденсатора равна 100 см2 Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.
Решение. Заряд Q одной пластины находится в поле, созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила (рис. 14.4)
F=E1Q,, (1)
где E1 — напряженность поля, создаваемого зарядом одной пластины. Но 
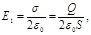где s – поверхностная плотность заряда пластины.
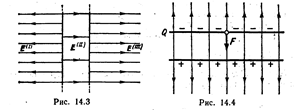
Формула (1) с учетом выражения для E1 примет вид
F = Q2 /(2e 0S).
Подставив значения величин Q, e 0 и S в эту формулу и произведя вычисления, получим
F =565 мкН.
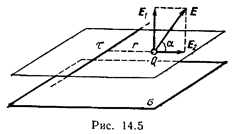
Пример 4. Электрическое поле создано, бесконечной плоскостью, заряженной с поверхностной плотностью s = 400 нКл/м 2, и бесконечной прямой нитью, заряженной с линейной плотностью t=100 нКл/м. На расстоянии r =10 см от нити находится точечный заряд Q =10 нКл. Определить силу, действующую на заряд, ее направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости.
Решение. Сила, действующая на заряд, помещённый в поле,
F=EQ, (1)
где Е — напряженность поля в точке, в которой находится заряд Q.
Определим напряженность Е поля, создаваемого, по условию задачи, бесконечной заряженной плоскостью и бесконечной заряженной нитью. Поле, создаваемое бесконечной заряженной плоскостью, однородно, и его напряженность в любой точке
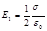. (2)
Поле, создаваемое бесконечной заряженной линией, неоднородно. Его напряженность зависит от расстояния и определяется по формуле
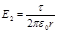. (3)
Согласно принципу суперпозиции электрических полей, напряженность поля в точке, где находится заряд Q, равна векторной сумме напряженностей E 1 и Е 2 (рис. 14.5): E = E 1 + E 2. Так как векторы E 1 и Е 2 взаимно перпендикулярны, то
.
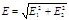Подставляя выражения E1 и E2 по формулам (2) и (3) в это равенство, получим
,
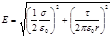или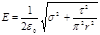 
.
Теперь найдем силу F, действующую на заряд, подставив выражение Е в формулу (1):
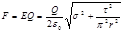. (4)
Подставив значения величин Q, e 0, s, t, p и r в формулу (4) и сделав вычисления, найдем
F =289 мкН.
Направление силы F, действующей на положительный заряд Q, совпадает с направлением вектора напряженности Е поля. Направление же вектора Е задается углом a к заряженной плоскости. Из рис. 14.5 следует, что
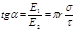, откуда 
.
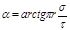Подставив значения величин p, r, s и t в это выражение и вычислив, получим
a=51°3¢
Пример 5. Точечный заряд Q =25 нКл находится в ноле, созданном прямым бесконечным цилиндром радиусом R= 1 см, равномерно заряженным с поверхностной плотностью s=2 мкКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r =10 см.
Решение. Сила, действующая на заряд Q, находящийся в поле,
F=QE, (1)
где Е — напряженность поля в точке, в которой находится заряд Q.
Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра
E =t/(2pe 0r), (2)
где t — линейная плотность заряда.
Выразим линейную плотность t через поверхностную плотность s. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q1 двумя, способами:
Q1=sS=s2pRl и Q 1 =t l.
Приравняв правые части этих равенств, получим t l =2p Rls. После сокращения на l найдем t=2p Rs. С учетом этого формула (2) примет вид E=Rs/(e0r). Подставив это выражение Е в формулу (1), найдем искомую силу:
F=QsR/(e0r). (3)
Так как R и r входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах.
Выполнив вычисления по формуле (3), найдем
F =25×10-9×2×10-6×10-2/(8,85×10-12×10×10-2)H==565×10-6H=565мкH.
Направление силы F совпадает с направлением вектора напряженности Е, а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.
Пример 6. Две концентрические проводящие сферы радиусами R1 =6 см и R2= 10 см несут соответственно заряды Q1 =l нКл и Q2 = –0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r1 =5 см, r2 =9 см r3 =15см. Построить график Е(r).
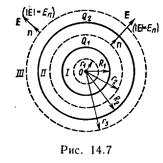Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 14.7): область I (r < R1), область II (R1 < r2 < R2), область III (r3 > R2).
1. Для определения напряженности E1 в области I проведем сферическую поверхность S1 радиусом r1 и воспользуемся теоремой Остроградского—Гаусса. Так как внутри области I зарядов нет, то согласно указанной теореме получим равенство
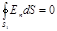, (1)
где En — нормальная составляющая напряженности электрического поля.
Из соображений симметрии нормальная составляющая En должна быть равна самой напряженности и постоянна для всех точек сферы, т. е. En=E1= const. Поэтому ее можно вынести за знак интеграла. Равенство (1) примет вид
.
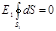Так как площадь сферы не равна нулю, то
E1 =0,
т. е. напряженность поля во всех точках, удовлетворяющих условию r1<.R1, будет равна нулю.
2. В области II сферическую поверхность проведем радиусом r2. Так как внутри этой поверхности находится, заряд Q1,тодля нее, согласно теореме Остроградского—Гаусса,можно записать равенство
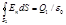. (2)
Так как En = E2 =const, то из условий симметрии следует
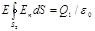, или ES2 = Q1 /e 0,
откуда
E2 = Q1 /(e 0 S 2).
Подставив сюда выражение площади сферы, получим
E2 = Q /(4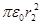 
). (3)
3. В области III сферическую поверхность проведем радиусом r3. Эта поверхность охватывает суммарный заряд Q1 + Q2. Следовательно, для нее уравнение, записанное на основетеоремыОстроградского — Гаусса, будет иметь вид
.
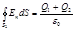Отсюда, использовав положения, примененные в первых двух случаях, найдем
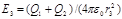. (4)
Убедимся в том, что правые части равенств (3) и (4) дают единицу напряженности электрического поля;
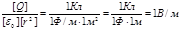
Выразим все величины в единицах СИ (Q1 =10-9 Кл, Q2 = –0,5´10-9 Кл, r1 =0,09 м, r2 =15м, l/(4pe 0)=9×109 м/Ф) и произведем вычисления:
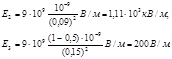
4. Построим график E (r). В области I (r1<R1) напряженность E =0. В области II (R1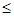 
r<.R2) напряженность E2 (r) изменяется по закону l/r 2. В точке r=R1 напряженность E2 (R1)=Q 1 /(4pe 0R 
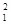)=2500 В/м.В точке r=R1 (r стремится к R1 слева) E2(R2)=Q1 /(4pe 0R 
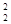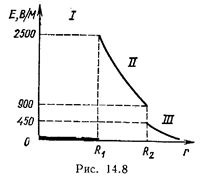
)=900В/м. В области III (r > R2) E3 (r) изменяется по закону 1/ r2, причем в точке r=R2 (r стремится к R2 справа) Е3(R2) =(Q1–|Q2 |)/(4pe 0R 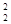)=450 В/м. Таким образом, функция Е (r) в точках r = R1 и r=R2 терпит разрыв. График зависимости Е(r) представлен на рис. 14.8.