ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОЛЕ

Основные формулы

· Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду;

j=П/ Q,

или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:

j= A/Q.

Потенциал электрического поля в бесконечности условно принят равным нулю.

Отметим, что при перемещении заряда в электрическом поле работа A_в.с внешних сил равна по модулю работе A_с.п сил поля и противоположна ей по знаку:

A_в.с= – A_с.п.

· Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,

.

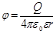· Потенциал электрического поля, создаваемого металлической, несущей заряд Q сферой радиусом R, на расстоянии гот центра сферы:

внутри сферы (r < R) ;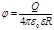

на поверхности сферы (r = R)

;

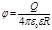вне сферы (r>R) .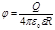

Во всех приведенных для потенциала заряженной сферы формулах e есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

· Потенциал электрического поля, созданного системой п точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраическойсуммепотенциалов j ₁, j ₂,..., j _n, создаваемых отдельными точечными зарядами Q₁, Q₂,..., Q_n:

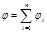
· Энергия W взаимодействия системы точечных зарядов Q₁, Q₂,..., Q_n определяется работой, которую эта система зарядов может совершить при удаленииих относительно друг друга в бесконечность, и выражается формулой

,

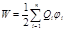где j _i — потенциал поля, создаваемого всеми п– 1 зарядами (за исключением 1-го) в точке, где расположен заряд Q_i.

· Потенциал связан с напряженностью электрического поля соотношением

Е = –gradj.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

,

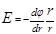или в скалярной форме

,

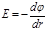а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению,

E =(j ₁ –j ₂,)/ d,

где j ₁ и j ₂ — потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.

· Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал j ₁, в другую, имеющую потенциал j ₂,

A = Q (j ₁ —j ₂), или ,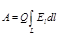

где E_l — проекция вектора напряженности Е на направление перемещения; dl — перемещение.

В случае однородного поля последняя формула принимает вид

A=QElcosa,

где l — перемещение; a — угол между направлениями вектора Е и перемещения l.

 

Примеры решения задач

 

Пример 1. Положительные заряды Q₁ =3 мкКл и Q₂ =20 нКл находятся в вакууме на расстоянии r₁ =l,5 м друг от друга. Определить работу A, которую надо совершить, чтобы сблизить заряды до расстояния r₂ =1 м.

Решен и е. Положим, что первый заряд Q₁ остается неподвижным, а второй Q₂ под действием внешних сил перемещается в поле, созданном зарядом Q₁, приближаясь к нему с расстояния r₁ =t,5 м до r₂ =1 м.

Работа А' внешней силы по перемещению заряда Q из однойточки поля с потенциалом j ₁ в другую, потенциал которой j ₂, равна по модулю и противоположна по знаку работе А сил поля по перемещению заряда между теми же точками:

А'= —А.

Работа А сил поля по перемещению заряда A = Q (j ₁ —j ₂). Тогда работа А' внешних сил может быть записана в виде

A' = – Q (j ₁ —j ₂)= Q (j ₂ — j₁). (1)

Потенциалы точек начала и конца пути выразятся формулами

; .

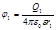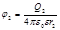Подставляя выражения j ₁ и j ₂ в формулу (1) и учитывая, что для данного случая переносимый заряд Q = Q₂, получим

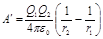. (2)

Если учесть, что 1/(4pe ₀)=9×10 ⁹ м/Ф, то после подстановки значений величин в формулу (2) и вычисления найдем

A '=180 мкДж.

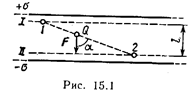
Пример 2. Найти работу А поля по перемещению заряда Q =10 нКл из точки 1 в точку 2 (рис. 15.1), находящиеся между двумя разноименно заряженными с поверхностной плотностью s=0,4 мкКл/м ² бесконечными параллельными плоскостями, расстояние l между которыми равно 3 см.

Решение. Возможны два способа решения задачи.

1-й способ. Работу сил поля по перемещению заряда Q из точки 1 поля с потенциалом j ₁ в точку 2 поля с потенциалом j ₂ найдем по формуле

A = Q (j ₁ —j ₂). (1)

Для определения потенциалов в точках 1 и 2 проведем через эти точки эквипотенциальные поверхности I и II. Эти поверхности будут плоскостями, так как поле между двумя равномерно заряженными бесконечными параллельными плоскостями однородно. Для такого поля справедливо соотношение

j ₁ —j ₂ = El, (2)

где Е — напряженность поля; l — расстояние между эквипотенциальными поверхностями.

Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E =s/e ₀. Подставив это выражение Е в формулу (2) и затем выражение j ₁ —j ₂ в формулу (1), получим

A=Q(s/e₀)l.

2-й способ. Так как поле однородно, то сила, действующая на заряд Q, при его перемещении постоянна. Поэтому работу перемещения заряда из точки 1 в точку 2 можно подсчитать по формуле

A =F Dr cosa, (3)

где F — сила, действующая на заряд; D r — модуль перемещения заряда Q из точки 1 в точку 2; a — угол между направлениями перемещения и силы. Но F=QE=Q(s/e₀). Подставив это выражение F в равенство (3), а также заметив, что D r cosa= l, получим

A = Q (s/e ₀) l. (4)

Таким образом, оба решения приводят к одному и тому же результату.

Подставив в выражение (4) значение величин Q, s, e ₀ и l, найдем

A =13,6 мкДж.

Пример 3. Электрическое поле создана длинным цилиндром радиусом R= 1см, равномерно заряженным с линейной плотностью t=20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях a₁ =0,5 см и а₂ =2 см от поверхности цилиндра, в средней его части.

Решение. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала Е = —gradj. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

Е= –( dj/d r), или dj= — Е d r.

Интегрируя последнее выражение, найдем разность потенциалов двух точек, отстоящих на r₁ и r₂ от оси цилиндра;

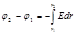. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой 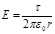. Подставив это выражение Е в равенство (1), получим

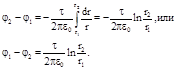(2)

Так как величины r₂ и r₁ входят в формулу в виде отношения, то их можно выразить в любых, но только одинаковых единицах:

r₁=R+a₁= 1,5 см; r₂ = R + a₂ =3см.

Подставив значения величия t, e ₀, r₁ и r₂ в формулу (2) и вычислив, найдем

j ₁ —j ₂ =250 В.

Пример 4. Электрон со скоростью v=1,83×10⁶ м/с влетел в однородное электрическое поле в направлении, противоположном вектору напряженности поля. Какую разность потенциалов U должен пройти электрон, чтобы обладать энергией E_i =13,6 эВ*? (Обладая такой энергией, электрон при столкновении с атомом водорода может ионизировать его. Энергия 13,6 эВ называется энергией ионизации водорода.)

Решение. Электрон должен пройти такую разность потенциалов U, чтобы приобретенная при этом энергия W в сумме с кинетической энергией T, которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации E_i, т. е. W+T=E_i. Выразив в этой формуле W=eU и Т =(m v ² /2), получим eU +(m v ² /2)= E_i. Отсюда .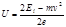

___________________

* Электрон-вольт (эВ) — энергия, которую приобретает частица, имеющая заряд, равный заряду электрона, прошедшая разность потенциалов 1 В. Эта внесистемная единица энергии в настоящее время допущена к применению в физике.

Произведем вычисления в единицах СИ:

U=4,15 В.

Пример 5. Определить начальную скорость υ ₀сближения про­тонов, нахо­дя­щихся на достаточно большом расстоянии друг от друга, если минимальное расстояние r _min, на которое они могут сблизиться, равно 10^-11 см.

Р е ш е н и е. Между двумя протонами действуют силы оттал­кивания, вслед­ствие чего движение протонов будет замедленным. Поэтому задачу можно ре­шить как в инерциальной системе коор­динат (связанной с центром масс двух протонов), так и в неинер­циальной (связанной с одним из ускоренно движу­щихся протонов). Во втором случае законы Ньютона не имеют места. Примене­ние же принципа Даламбера затруднительно из-за того, что ускорение системы будет переменным. Поэтому удобно рассмотреть задачу в инерциальной сис­теме отсчета.

Поместим начало координат в центр масс двух протонов. По­скольку мы имеем дело с одинаковыми частицами, то центр масс будет находиться в точке, делящей пополам отрезок, соединяющий частицы. Относительно центра масс частицы будут иметь в любой момент времени одинаковые по модулю скоро­сти. Когда частицы находятся на достаточно большом расстоянии друг от друга, скорость υ ₁каждой частицы равна половине υ ₀, т. е. υ ₁ =υ ₀ /2.

Для решения задачи применим закон сохранения энергии, со­гласно кото­рому полная механическая энергия Е изолированной системы постоянна, т. е.

Е=Т+ П,

где Т - сумма кинетических энергий обоих протонов относительно центра масс; П - потенциальная энергия системы зарядов.

Выразим потенциальную энергию в начальный П₁ и конечный П₂ моменты движения.

В начальный момент, согласно условию задачи, протоны нахо­дились на большом расстоянии, поэтому потенциальной энергией можно пренебречь (П₁=0). Следовательно, для начального момента полная энергия будет равна кинетической энергии T ₁протонов, т. е.

E=T _l. (1)

В конечный момент, когда протоны максимально сблизятся, скорость и кинети­ческая энергия равны нулю, а полная энергия будет равна потенциальной энер­гии П₂, т. е.

Е= П₂. (2)

Прирав­няв правые части равенств (1) и (2), получим

T₁=П₂. (3)

Кинети­ческая энергия равна сумме кинетических энергий про­тонов:

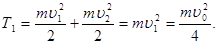(4)

Потенциальная энергия системы двух зарядов Q ₁ и Q ₂, находя­щихся в вакууме, определяется по формуле 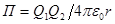, где r - расстоя­ние между зарядами. Воспользовавшись этой формулой, полу­чим

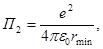(5)

С учетом равенств (4) и (5) формула (3) примет вид

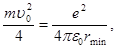откуда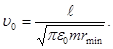

Выполнив вычисления по полученной формуле, найдем υ ₀ =2,35 Мм/с.

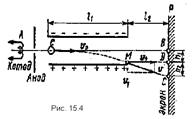
Пример 6. Электрон без на­чальной скорости прошел разность потен­циалов U ₀ =10 кВ и влетел в пространство между пластинами плоского конденсатора, заряжен­ного до разности потенциалов U _l=100 В, по ли­нии АВ, парал­лельной пластинам (рис. 15.4). Рас­стояние d между пла­стинами равно 2 см. Длина l ₁ ­пластин конденсатора в нап­равлении по­лета элек­трона, равна 20 cм. Определить рас­стояние ВС на экране Р, от­стоящем от конденсатора на l ₂=1 м.

Р е ш е н и е. Движение электрона внутри конденсато­ра складыва­ется из двух дви­жений: 1) по инерции вдоль линии АВ с постоянной скоро­стью υ ₀, приобретенной под действием разности потенциалов U ₀, кото­рую электрон прошел до конденсатора; 2) равномерно ускоренного дви­жения в вертикальном направлении к положительно заряженной пла­стине под действием постоянной силы поля конденсатора. По вы­ходе из конденсатора электрон будет двигаться равномерно со скоро­стью υ, которую он имел в точке М в момент вылета из кон­денсатора.

Из рис. 15.4 видно, что искомое расстояние | BC|=h ₁ +h ₂, где с h ₁ - рас­стояние, на которое сместится электрон в вертикальном направлении во время движения в конденсаторе; h ₂- расстояние между точкой D на эк­ране, в которую электрон попал бы, двигаясь по выходе из конденса­тора по направлению начальной скорости υ ₀, и точкой С, в которую электрон попадет в действительности.

Выразим отдельно h ₁ и h ₂. Пользуясь формулой длины пути равно­мерно ускоренного движе­ния, найдем

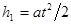. (1)

где а - ускорение, полученное электроном под действием поля конден­сатора; t- время полета электрона внутри конденсатора.

По второму закону Ньютона a=F/m, где F - сила, с которой поле дей­ствует на электрон; т- его масса. В свою очередь, F =eE=eU ₁ /d, где е - заряд электрона; U ₁ - разность потенциалов между пластинами конден­сатора; d - расстояние между ними. Время полета электрона внутри конденсатора найдем из фор­мулы пути равномерного движения 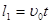, откуда

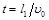
где l ₁- длина конденсатора в направлении полета электрона. Выраже­ние скорости найдем из условия равенства работы, совер­шенной полем при перемещении электрона, и приобретенной им кинетической энер­гии: 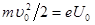. Отсюда

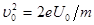(2)

Подставляя в формулу (1) последовательно значения а, F, t и υ ₀²из со­ответствующих выражений, получим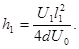

Длину отрезка h ₂найдем из подобия треугольников MDC и век­тор­ного:

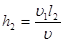(3)

где υ ₁ - скорость электрона в вертикальном направлении в точке М; l ₂- расстояние от конденсатора до экрана.

Скорость υ ₁ найдем по формуле υ ₁ =at, которая с учетом выра­жений для а, F и t примет вид

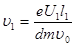
Подставив выражение υ ₁ в формулу (3), получим 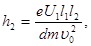, или, заменив υ ₀² по формуле (3), найдем

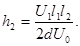
Окончательно для искомого расстояния | BC | будем иметь

| BC|= ­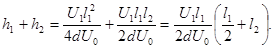

­Подставив значения величин U ₁, U ₀, d, l ₁ и l ₂ в последнее выражение и произведя вычисления, получим | BC |=5,5cм.