ЭЛEКTPИЧECКAЯ EMКOCTЬ. КOHДEHCATOPЫ

Основные формулы

· Электрическая емкость уединенного проводника или конден­сатора

C=Δ Q /Δφ,

где Δ Q - заряд, сообщенный проводнику (конденсатору); Δφ - ­изменение потенциала, вызванное этим зарядом.

· Электрическая емкость уединенной проводящей сферы радиу­сом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε,

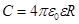
Если сфера полая и заполнена диэлектриком, то электроемкость ее от этого не изменяется.

· Электрическая емкость плоского конденсатора

,

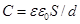где S - площадь пластин (каждой пластины); d - расстояние между ними; ε - диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного п слоями диэлектриком толщиной d _iкаждый с диэлектрическими про­ницаемостями ε, (слоистый конденсатор),

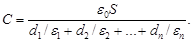
· Электрическая емкость сферического конденсатора (две концентрические сферы радиусами R ₁и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

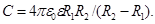
· Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R ₁и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

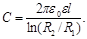
· Электрическая емкость С последовательно соединенных конденсаторов:

в общем случае 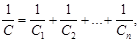где п - число конденсаторов;

в случае двух конденсаторов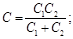

в случае п одинаковых конденсаторов с электроемкостью С₁ каж­дый

C=C ₁ /n.

· Электрическая емкость параллельно соединенных конденса­торов:

в общем случае C=C ₁ +C ₂ +...+C _n;

в случае двух конденсаторов C=C ₁ +C ₂;

в случае п одинаковых конденсаторов с электроемкостью С₁ каж­дый C=nC ₁. ­

Примеры решения задач

Пример 1. Определить электрическую емкость С плоского кон­денсатора с двумя слоями диэлектриков: фарфора толщиной d ₁ = 2 мм и эбонита толщиной d ₂ = 1,5 мм, если площадь S пластин равна 100 см².

Р е ш е н и е. Емкость конденсатора, по определению, C=Q/U, где Q - заряд на пластинах конденсатора; U - разность потенциалов пластин. Заменив в этом равенстве общую разность потенциалов U конденсатора суммой U ₁ +U ₂напряжений на слоях ди­электриков, получим

C=Q/ (U ₁ +U ₂). (1)

Приняв во внимание, что Q=σS, U ₁ = Е ₁ d _i= 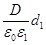и U ₂ =E ₂ d ₂ = 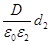, равенство (1) можно переписать в виде

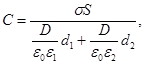(2)

где σ - поверхностная плотность заряда на пластинах; Е ₁ и Е ₂ - напряженности поля в первом и втором слоях диэлектрика соответственно; D - электрическое смещение поля в диэлектриках.

Умножив числитель и знаменатель равенства (2) на ε₀ и учтя, что D=σ, окончательно получим

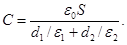
Ответ: С=98,3пФ

Пример 2. Два плоских конденсатора одинаковой электроемко­сти С ₁ =С ₂ =С соединены в батарею последовательно и подключены источнику тока с электродвижущей силой ε. Как изменится разность потенциалов U ₁ на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью ε =7?

Р е ш е н и е. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова: U ₁= U ₂ =ε/2. После заполнения электроемкость второго конденсатора возросла в ε раз:

C ₂'=ε C ₂=ε C.

Электроемкость С первого не изменилась, т. е. C ₁' =C.

Так как источник тока не отключался, то общая разность потен­циалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденсаторе

U ₁' =Q/C ₁' =Q/C, (1)

где Q - заряд на пластинах конденсатора. Поскольку при последовательном соединении конденсаторов заряд на каждой пластине и на всей батареи одинаков, то

Q = С' _бат ε

где 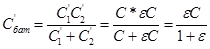. Таким образом,

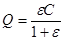ε.

Подставив это выражение заряда в формулу (1), найдем

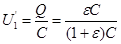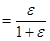ε ε.

Чтобы найти, как изменилась разность потенциалов на пластинах первого конденсатора, вычислим отношение:

U' ₁/ U ₁=2ε/(1+ε).

После подстановки значения ε получим

U' ₁/ U ₁=1,75.

Следовательно, разность потенциалов на пластинах первого конденсатора после заполнения второго конденсатора диэлектриком возросла в 1,75 раза.