Ременная передача
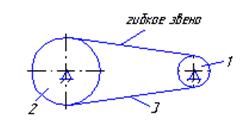
Механизмы с гидравлическим и пневматическим устройством
Кинематическое замыкание осуществляется жидкостью или газом, т.е. жидкость или газ звено.
Применение: В основном как усилители.
Механизмы с электрическим и электромагнитным устройством.
Механизм контроля ширины шлифовального круга:
Лекция №3
Классификация кинематических пар.
Кинематическая связь – это соприкосновение в кинематической паре.
Связь – это ограничение степеней свободы.
Условие кинематической связи – это совокупность ограничений связей, которые накладываются на относительное движение звеньев в кинематической паре при соприкосновении.
Пассивная связь – связь, которая не оказывает влияния на характер движения механизма.
Степень свободы – это показатель, определяющий возможность перемещения тела в пространстве.
В 3-х мерном пространстве – 6 степеней свободы.
В 2-х мерном (плоскость) – 3 степени свободы.
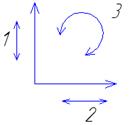
Основное условие синтеза механизма – это грамотное наложение связей для получения необходимого закона движения рабочего органа.
Условие существования кинематической пары:
1 ≤ S ≤ 5, S – число связей
=> Н= 6 – S, Н – число степеней свободы.
Классификация кинематических пар по количеству связей.
I, II, III, IV, V – класс пары.
Одна связь S=1 S= 6 - Н
Пять связей S=5
Примеры:
Шар на плоскости:
Н= 5 степень свободы
3-х мерная система
Цилиндр на плоскости:
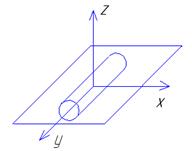
3-х мерная система
Объемный шарнир:
3-х мерная
Плоский шарнир:
2-х мерная
Н=1
S=5
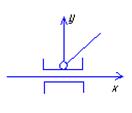
Плоская кулиса:
2-х мерная
Н=2, S=4.
3ПЛ – плоскостная кинематическая пара с 3-мя степенями свободы
число степеней обозначение
свободы
Структурная формула кинетической цепи общего вида (Определяет подвижность механизма):
Формула Чебышева
W = 6n -5p5 – 4p4 – 3p3 – 2p2 – p1 (для 3-х мерного пространства)
W – степень подвижности
n – количество подвижных звеньев
p5 – количество кинематических пар V класса
W = 3n - 2 p5 - p4 (для 2-х мерного пространства)
Пример:
n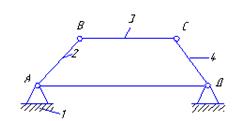 
= 3 (2, 3, 4)
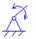Н = 1
S = 6 - 1=5
p5 = 4
p4 = p3 = p2 = p1 = 0
Кинематические пары: 1 -2, 2 -3, 3 -4, 4 -1
W = 3×3 - 2×4 = 1
Пример пассивной связи:
4 – не учитывать
Анализ W:
1. Условие целенаправленности работы (существование механизма):
W≥ 1 1) W = 0 – механизм ферма!
2) W< 0 – механизма не существует
2. Количество неизвестных обобщенных параметров равно W
Пример: 1) W = 1
φ(t) – необходимо знать, чтобы стать механизмом.
2)
W = 2
Необходимо знать φ1(t) и φ2(t).
Если φ2(t).=?, то это не механизм
Т. е. W определяет количество неизвестных обобщенных параметров для полной определенности и прогнозируемости работы механизма.
Определение W в механизмах:
1.Способ замены звеньев со сложной конфигурацией звеньев (т.е. высшими кинематическими парами).
А)
Б)
ВС = ρс(а)
п – п – нормаль к а в точке С
Лекция №4
Структурная классификация плоских механизмов (по Асуру).
+Пример разбиения механизма на группы Асура.
Семейство механизмов – это совокупность механизмов обладающих общими связями, т.е. каждый из механизмов может рассматриваться отдельно, но они обладают общей связью.
Семейства классифицируются по количеству общих связей.
1. Нулевое семейство: общих связей нет.
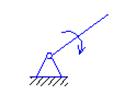
2.Первое семейство: одна связь.
Механизмы: 1 -2, 3 -4,
5 накладывает одну связь
3. Второе семейство:
Основной принцип образования механизмов (Асур, 1914 г.):
Схема любого механизма может быть составлена присоединением к ведущему звену механизмов с нулевой относительной степенью подвижности.
Для плоского механизма в присоединяемой группе p5 =3n/2 для пар только 5 класса (W = 0).
Пример:
Wотн (3,4,5,6)=3n - 2p5 – p4 = 3×4 - 2×6 = 0
W = 3×5 - 2×7 = 1
Анти - пример:
Механизм не работает
Wотн (3,4) = 3×2 - 2×3 = 0
W = 3×3 - 2×5 = 9-10=-1
Еще пример:
W = 1
5 не учитывается (пассивная связь)
Классификация механизмов по группам:
II III IV V (при p4=0)
Класс группы определяется количеством p5 = 3, 6, 9, 12, … присоединенных кинематических пар 5 класса.
Группа – это совокупность кинематических пар, образующих разомкнутую кинематическую цепь.
Порядок группы – число элементов, которыми группа присоединена к механизму.
1)Группа I класса (ведущее звено)
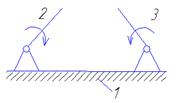
2)Группа II класса 2 порядка
р5 = 3(1-2, 2-3, 3-4)
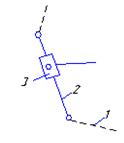
р5=3(1-2, 2-3, 3-4)
элементов присоединения - 2
3)Группа III класса 3 порядка
р5=6(1-2, 1-4, 1-5, 2-3, 4-3, 5-3)
элементов – 3
4)Группа IV класса 2 порядка
р5=9
элементов
Особенность: Четырехсторонний контур. За счет а ║ в + 3 связи, т.е. р5=6+3 (доп.)
Структурная формула механизма: [I(1-2) →II(3-4)]
Лекция №5
Кинематический анализ механизмов.
Задача: Изучение и анализ движения звеньев механизма без учета сил.
Мгновенный центр скоростей:
Абсолютный – центр скоростей звена в абсолютном движении (относительно неподвижного звена).
Относительный – центр скоростей звена (относительно подвижного звена).
Центр (полюс) – это воображаемая точка пространства относительно которой звено совершает движение.
Основная теорема:
Действует во всех случаях.
Обозначение
Р42–относительный центр скоростей. Центр скоростей 4-го звена относительно 2-го.
Пример:
Применение: Мгновенный центр скоростей звена, совершающий поступательные движения находится на перпендикуляре к траектории движения центра тяжести этого звена!
Понятие центроиды:
Центроида – это воображаемая кривая, определяющаяся положением мгновенных центров скоростей во времени.
Соотношение между скоростями звеньев механизма:
Примечание: Пояснить важные определения соотношения скоростей.
Пример 1:
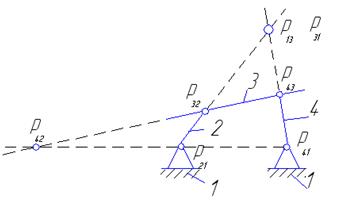
ω41 / ω21 = Р21×Р42 / Р41×Р42
Относительные и абсолютные скорости звеньев механизма обратно пропорциональны длинам отрезков, соединяющих абсолютные центры скоростей этих звеньев с центром скоростей в их относительном движении!
Основная теорема кинематики: Соотношение абсолютных скоростей звеньев обратно пропорционально расстоянию между абсолютными центрами скоростей этих звеньев и относительными центрами скоростей этих звеньев.
Самостоятельно дать всем на определение ω31 / ω41 = Р41×Р34 / Р31×Р34!
И дать ответ Р34=Р43! – Принцип относительности.
Пример 2:
Механизм мальтийского креста.
Заменяющая смена.
р42 – р31
р21 – р31
2 – 3
i23 = ω21 / ω31 = Р31×Р32 / Р21×Р32!
Теорема: Относительный центр скоростей двух звеньев лежит в точке пересечения нормали к точке касания звеньев и оси на которой лежат центры их абсолютных скоростей.