| Наименование показателя | Принятые наименования | Формула |
| Множественный R | Коэффициент множественной корреляции |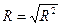 
|
| R-квадрат | Коэффициент детерминации R2 |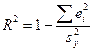 
|
| Нормированный R-квадрат | Скорректированный R2 |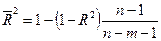 
|
| Стандартная ошибка | Среднеквадратическое отклонение от модели |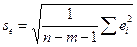 
|
| Наблюдения | Количество наблюдений n | n |
Дисперсионный анализ
| df | SS – сумма квадратов | MS – среднее значение | F-критерий Фишера | Значимость F | |
| Регрессия |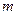 
| 
| 
| 
| 
|
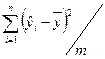
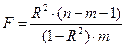
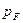
| Остаток |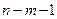 
| 
| 
| ||
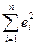
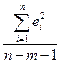
| Итого |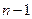 
| 
|
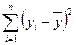
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | b 0 |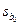 
| 
| 
|
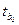
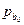
| x1 | b 1 |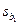 
| 
| 
|
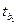
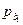
| x2 | b 2 |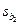 
| 
| 
|
| … | … | … | … | … |
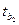
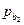
В таблице «Регрессионная статистика» расположены множественный коэффициент корреляции, коэффициент детерминации, нормированный коэффициент детерминации, стандартная ошибка и количество наблюдений. Таблица «Дисперсионный анализ» в столбце df содержит число независимых переменных, количество степеней свободы, в столбце SS – объясненную сумму квадратов, сумму квадратов остатков и общую сумму квадратов результативного фактора, в столбце MS находятся объясненная сумма квадратов и сумма квадратов остатков на одну степень свободы, в столбце F – расчетное значение статистики Фишера. В столбце значимость F расположена вероятность ошибки расчета, если это значение меньше уровня значимости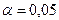 
, то Fрасч > Fкр.
В третьей таблице в столбце Коэффициенты находятся свободный коэффициент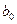 
и коэффициенты при переменных 
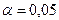уравнения регрессии. Каждому коэффициенту соответствует значение t -статистики (третий столбец таблицы). P-Значение показывает вероятность ошибки расчета t -статистики, причем если P-Значение меньше уровня значимости , то tрасч > tкр.
Приложение 2
Расчет критических значений t и F.
Значение tкр можно получить при помощи статистической функции, которая имеет формат СТЬЮДРАСПОБР(< 
>; < n – m – 1>), где α – уровень значимости, по умолчанию α = 0,05; n – число наблюдений; m – количество независимых переменных в модели. Устанавливаем курсор в пустой ячейке. Вызываем команду ВСТАВКА – ФУНКЦИЯ – СТАТИСТИЧЕСКИЕ (рис. 5.1). Выбираем функцию СТЬЮДРАСПОБР и вводим значения вероятности и количества степеней свободы (рис. 5.2).
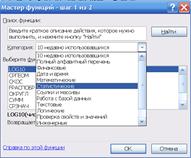Рис. 5.1. Мастер функций
| 
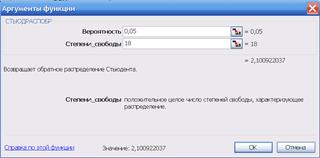Рис. 5.2. Функция СТЬЮДРАСПОБР
|
Значение Fкр можно получить при помощи статистической функции, которая имеет формат FРАСПОБР(< >; < m >; < n – m – 1>), где α – уровень значимости, по умолчанию α = 0,05; n – число наблюдений; m – количество независимых переменных в модели. Вызываем команду ВСТАВКА – ФУНКЦИЯ – СТАТИСТИЧЕСКИЕ – FРАСПОБР (рис. 5.3).
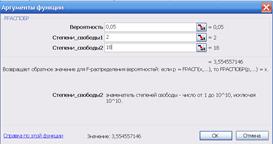
Рис. 5.3. Функция FРАСПОБР
Приложение 3
Значения статистик Дарбина-Уотсона при 5%-м уровне значимости.
| n | k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | |||||
| dL | dU | dL | dU | dL | dU | dL | dU | dL | dU | |
| 0,61 | 1,40 | |||||||||
| 0,70 | 1,36 | 0,47 | 1,90 | |||||||
| 0,76 | 1,33 | 0,56 | 1,78 | 0,37 | 2,29 | |||||
| 0,82 | 1,32 | 0,63 | 1,70 | 0,46 | 2,13 | |||||
| 0,88 | 1,32 | 0,70 | 1,64 | 0,53 | 2,02 | |||||
| 0,93 | 1,32 | 0,66 | 1,60 | 0,60 | 1,93 | |||||
| 0,97 | 1,33 | 0,81 | 1,58 | 0,66 | 1,86 | |||||
| 1,01 | 1,34 | 0,86 | 1,56 | 0,72 | 1,82 | |||||
| 1,05 | 1,35 | 0,91 | 1,55 | 0,77 | 1,78 | |||||
| 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 | 0,69 | 1,97 | 0,56 | 2,21 | |
| 1,10 | 1,37 | 0,98 | 1,54 | 0,86 | 1,73 | 0,74 | 1,93 | 0,62 | 2,15 | |
| 1,13 | 1,38 | 1,02 | 1,54 | 0,90 | 1,71 | 0,78 | 1,90 | 0,67 | 2,10 | |
| 1,16 | 1,39 | 1,05 | 1,53 | 0,93 | 1,69 | 0,82 | 1,87 | 0,71 | 2,06 | |
| 1,18 | 1,40 | 1,08 | 1,53 | 0,97 | 1,68 | 0,86 | 1,85 | 0,75 | 2,02 | |
| 1,20 | 1,41 | 1,10 | 1,54 | 1,00 | 1,68 | 0,90 | 1,83 | 0,79 | 1,99 | |
| 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,67 | 0,93 | 1,81 | 0,83 | 1,96 | |
| 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 | |
| 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 | |
| 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 | |
| 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 | |
| 1,30 | 1,46 | 1,22 | 1,55 | 1,14 | 1,65 | 1,06 | 1,76 | 0,98 | 1,88 | |
| 1,32 | 1,47 | 1,24 | 1,56 | 1,16 | 1,65 | 1,08 | 1,76 | 1,01 | 1,86 | |
| 1,33 | 1,48 | 1,26 | 1,56 | 1,18 | 1,65 | 1,10 | 1,75 | 1,03 | 1,85 | |
| 1,34 | 1,48 | 1,27 | 1,56 | 1,20 | 1,65 | 1,12 | 1,74 | 1,05 | 1,84 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 | 1,14 | 1,74 | 1,07 | 1,83 |
k – количество независимых переменных, n – количество наблюдений.
СПИСОК ЛИТЕРАТУРЫ
1. Бородич С.А. Эконометрика / Учебное пособие для ВУЗов. - Мн.: Новое знание, 2004.
2. Доугерти К. Введение в эконометрику. Пер. с англ. М.: ИНФРА-М, 1999.
3. Елисеева И.И. Эконометрика. М., 2008.
4. Кремер Н.Ш., Путко Б.А. Эконометрика. Юнити-Дана, 2008.
5. Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. начальный курс. М., Дело, 2004.
6. Орлова И.В., Половников В.А. Экономико-математические методы и модели. Компьютерное моделирование. М., 2009.
7. Экономико-математические методы и модели. Практикум. Под ред. Миксюк С.Ф. Мн, БГЭУ, 2008.