Шаг 0. Подготовительная работа.
Занесем статистические данные в электронную таблицу по столбцам (см. рис. 1.1).
Шаг 1. Подобрать наилучшую форму связи между результативным и независимым фактором при помощи построения диаграммы рассеяния.
Вызываем команду ВСТАВКА – ДИАГРАММА. Появится меню МАСТЕР ДИАГРАММ шаг 1 из 4 (рис. 2.1).
Рис. 2.1. Шаг 1 меню МАСТЕРА ДИАГРАММ
Выбираем вид диаграммы: точечная. Нажимаем кнопку ДАЛЕЕ. Появится меню Шаг 2 из 4: выбор диапазона исходных данных (рис. 2.2).
Рис. 2.2. Выбор диапазона исходных данных
| 
Рис. 2.3. Закладка РЯД меню МАСТЕРА ДИАГРАММ
|
Установим курсор в окошко Диапазон и выделим курсором мыши диапазон исходных данных (см. рис. 2.2). Ряды: в столбцах. Компьютер распознает первый столбец исходных данных как независимую переменную, поэтому перейдем в закладку РЯД и проверим, чтобы Значения X и Значения Y соответствовали данным рабочей таблицы (см. рис. 2.3). Нажимаем кнопку ДАЛЕЕ.
Шаг 3 из 4: параметры вывода. Можно установить различные параметры оформления диаграммы. Кнопка ДАЛЕЕ. Шаг 4 из 4: определяем, где поместить диаграмму. Нажимаем кнопку ГОТОВО. Диаграмма рассеяния для рассматриваемого примера представлена на рис. 2.4.
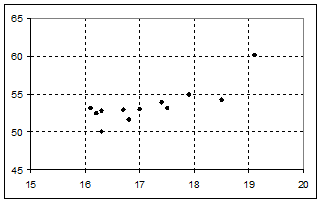
Рис. 2.4. Диаграмма рассеяния
Построим линию тренда. Выделим поле диаграммы. Меню: ДИАГРАММА – ДОБАВИТЬ ЛИНИЮ ТРЕНДА. Появится меню: ЛИНИЯ ТРЕНДА (рис. 2.5). Выберем любой тип линии тренда, кроме типа «Линейная фильтрация». Начнем с линейного. Зайдем на закладку: ПАРАМЕТРЫ(рис. 2.6) и установим флажки: Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации.
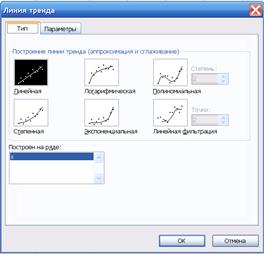Рис. 2.5. Выбор типа линии тренда
| 
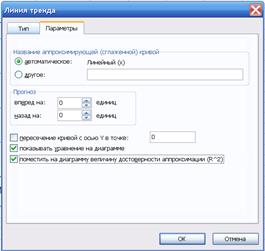Рис. 2.6. Установка параметров линии тренда
|
После нажатия кнопки ОК на графике появится линия тренда, ее уравнение и коэффициент детерминации (см. рис. 2.7).
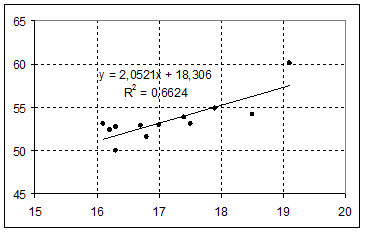
Рис. 2.7. Линия тренда
Уравнение, которое отражено на диаграмме, должно совпадать с тем уравнением, которое мы построили при помощи АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ при выполнении соответствующего варианта лабораторной работы № 1.
Далее, чтобы подобрать нужный вид линии тренда по коэффициенту детерминации R 2, устанавливаем курсор мыши на линии тренда и нажимаем правую клавишу. Появится контекстное меню, из которого нужно выбрать: ФОРМАТ ЛИНИИ ТРЕНДА (см. рис. 2.8). Выберем другой тип линии в меню ЛИНИЯ ТРЕНДА. Например, логарифмическая. Запишем получившееся уравнение и коэффициент детерминации. Затем снова воспользуемся контекстным меню для получения аналогичных данных по полиномиальной 2-й степени, степенной и экспоненциальной линии тренда.
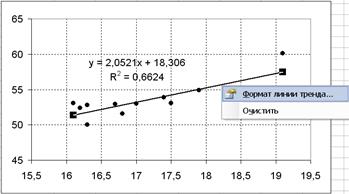
Рис. 2.8. Вход в меню «Формат линии тренда»
Шаг 2. Построить нелинейные регрессионные модели при помощи команды АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ. Выбрать наилучшую из них
Построим рабочую таблицу (рис. 2.9).
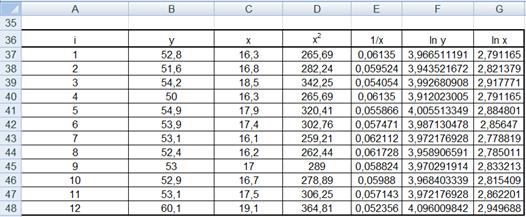
Рис. 2.9. Рабочая таблица для построения
нелинейных регрессионных моделей
Встроенная команда РЕГРЕССИЯ использует алгоритм для нахождения параметров только линейного уравнения, поэтому перед ее использованием выбранный вид нелинейного уравнения регрессии следует привести к линейному виду. Воспользуемся данными таблицы 2.1.
Таблица 2.1.
| № п.п. | Вид уравнения | Входной интервал y | Входной интервал x |
| 1. | Логарифмическое
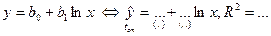
| y | ln x |
| 2. | Полиномиальное 2 степени
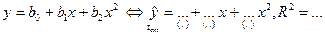
| y | x, x 2 |
| 3. | Степенное
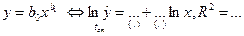
| ln y | ln x |
| 4. | Экспоненциальное
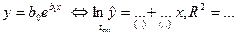
| ln y | x |
| 5. | Гиперболическое
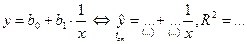
| y | 1 / x |
Построим, например, логарифмическое уравнение. Для этого в меню АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ введем данные столбца y и столбца ln x. Входной интервал Y: B36:B48; Входной интервал X: G36:G48 (см. рис. 2.9 и 2.10).
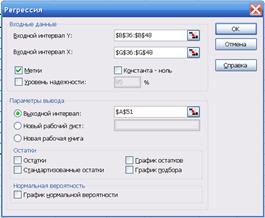
Рис. 2.10. Использование меню РЕГРЕССИЯ при построении уравнения
с логарифмической формой связи
Результаты расчетов (рис. 2.11) запишем, и произведем аналогичные расчеты для построения полиномиальной, степенной, экспоненциальной и гиперболической формы связи, изменяя в меню РЕГРЕССИЯ соответствующие входные и выходные данные.
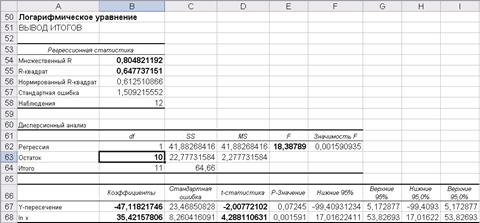
Рис. 2.11. Результаты расчетов для уравнения
с логарифмической формой связи
Для данных примера 2 получены результаты, представленные в таблице 2.2.
Таблица 2.2
| № п.п. | Уравнение регрессии | Примечания |
| 1. | Логарифмическое
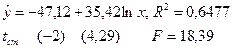
| Уравнение удовлетворительного качества, однако хуже экспоненциального. |
| 2. | Полиномиальное 2 степени
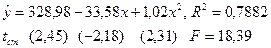
| Наибольший R 2, однако коэффициент при x статистически незначим. |
| 3. | Степенное
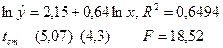
| Уравнение удовлетворительного качества, однако хуже экспоненциального. |
| 4. | Экспоненциальное
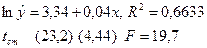
| Второй по величине R 2, коэффициент при x статистически значим. Наилучшее из всех уравнений. |
| 5. | Гиперболическое
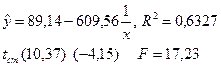
| Уравнение удовлетворительного качества, однако хуже экспоненциального. |
Шаг 3. Найти прогнозное значение результата по наилучшему из построенных уравнений.
Итак, мы выбрали экспоненциальное уравнение (см. табл. 2.2). Выразим y через x в явном виде: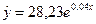 
. Рассчитаем прогноз: 
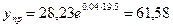тыс. д.е. Значит, если инвестиции будут равны 19,5 тыс. д.е., то объем производства должен составить 61 тыс. 580 ед.
Шаг 4. Оформление отчета.
План отчета.
1. Укажите фамилию, имя, название группы, номер варианта.
2. Запишите все уравнения, полученные при помощи диаграммы рассеяния с коэффициентами детерминации. Выберите наилучшее из них.
3. Запишите все уравнения, полученные при помощи АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ со всеми статистиками. Выберите наилучшее из них. Объясните свой выбор.
4. Совпали ли выбранные в п.2 и п.3 уравнения?
5. Рассчитайте прогноз при помощи уравнения наилучшего качества. Дайте экономическую интерпретацию параметров уравнения.
Лабораторная работа № 3.
ПОСТРОЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИОННОЙ МОДЕЛИ
Постановка задачи: известны статистические данные наблюдений за некоторым количеством однородных экономических объектов.
Требуется:
1. Осуществить выбор факторных признаков для построения двухфакторной (или трехфакторной) регрессионной модели.
2. Построить линейное уравнение регрессии, описывающее зависимость между факторами и результатом.
3. Оценить качество уравнения регрессии с экономической и математической точки зрения.
4. Найти прогнозное значение результата.
ВАРИАНТЫЗАДАНИЙ
Вариант 1
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл.3.1). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 112% от их среднего уровня.
Таблица 3.1
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
| i | y | x 1 | x 2 | x 3 |
Вариант 2
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл. 3.2). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 92% от их среднего уровня.
Таблица 3.2
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
| i | y | x 1 | x 2 | x 3 |
Вариант 3
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл. 3.3). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 106% от их среднего уровня.
Таблица 3.3
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
| i | y | x 1 | x 2 | x 3 |
Вариант 4
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл. 3.4). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 89% от их среднего уровня.
Таблица 3.4
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
Вариант 5
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл. 3.5). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 115% от их среднего уровня.
Таблица 3.5
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
Вариант 6
По данным 30 наблюдений постройте модель множественной регрессии удовлетворительного качества (табл. 3.6). Рассчитайте прогноз результата, если прогнозные значения независимых факторов будут составлять 90% от их среднего уровня.
Таблица 3.6
| № | Валовой продукт, млн. руб. | Балансовая стоимость оборудования, млн. руб. | Объем промышленного производства, млн. руб. | Количество занятых, тыс.чел. |
| i | y | x 1 | x 2 | x 3 |
Пример 3. Известны статистические данные 16 наблюдений некоторых экономических показателей (табл. 3.7). Постройте линейное уравнение регрессии, описывающее зависимость между факторами и результатом для предсказания объема реализации продукта, если прогнозный объем факторных признаков должен составить 120% от их среднего уровня.
Таблица 3.7
| Объем реализации товара, млн. руб. | Расходы на оформление товара, руб. | Расходы на рекламу, руб. | Цена товара, руб. | Индекс потребительских расходов, % |
| y | x 1 | x 2 | x 3 | x 4 |
| y | x 1 | x 2 | x 3 | x 4 |