Порядок выполнения работы. Занесем имеющиеся статистические данные в электронную таблицу (рис

Шаг 0. Подготовительная работа.

Занесем имеющиеся статистические данные в электронную таблицу (рис. 4.1).

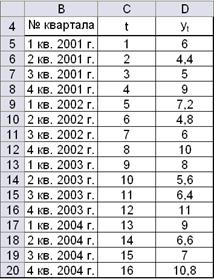
Рис. 4.1. Исходные данные

Шаг 1. Построить график динамики уровней ряда.

Построение графика динамики уровней ряда произведем при помощи функции МАСТЕР ДИАГРАММ. Вызываем меню ВСТАВКА – ДИАГРАММА – ГРАФИК.

В качестве диапазона выберем столбец, содержащий значения фактора y_t. В нашем случае диапазон D5:D20 (см. рис. 4.1). Закладка РЯД позволяет добавлять графики значений других рядов или наборов данных. В качестве значений независимой переменной по умолчанию устанавливаются номера наблюдений t.

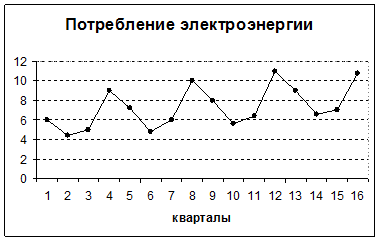
Рис. 4.2. График динамики потребления электроэнергии

Изучая график потребления электроэнергии (рис. 4.2), заметим наличие сезонных колебаний с периодом 4 квартала и возрастающую тенденцию в уровнях ряда.

Шаг 2. Рассчитать значения сезонных компонент методом скользящей средней.

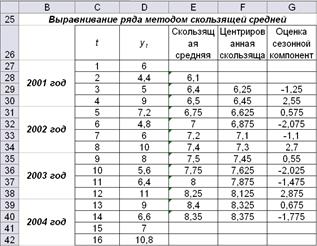
Рис. 4.3. Рабочая таблица расчета сезонных компонент

методом скользящей средней

Составим рабочую таблицу (см. рис. 4.3). Поскольку в нашем случае известны поквартальные данные (длина цикла равна 4), то найдем скользящие средние для каждой группы из четырех соседних значений уровней ряда. Для этого используем функцию СРЗНАЧ (ВСТАВКА – ФУНКЦИЯ – СТАТИСТИЧЕСКИЕ – СРЗНАЧ). Запишем функцию в ячейке E28 = СРЗНАЧ(D27:D30) и скопируем вниз до ячейки E40.

Центрированные скользящие средние находим, чтобы привести данные в соответствие с фактическими моментами времени. Они находятся как средние значения между парами соседних скользящих средних. Например, в ячейке F29 рассчитано среднее между значениями ячеек E28 и E29. Затем функцию можно скопировать вниз по столбцу.

Оценки сезонной компоненты для аддитивной модели рассчитаем как разность между фактическими уровнями ряда и центрированными скользящими средними. В нашем примере G29 = D29 – F29 и т.д. Если нужно построить мультипликативную модель, то фактические уровни ряда делятся на центрированную скользящую среднюю.

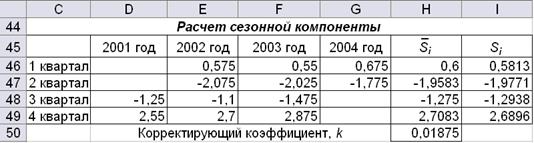
Рис. 4.4. Расчет сезонных компонент

В следующей таблице (см. рис. 4.4) рассчитаем оценки сезонных компонент, распределенных по кварталам. Чтобы не заполнять таблицу вручную, воспользуемся командой ПРАВКА – СПЕЦИАЛЬНАЯ ВСТАВКА. Для этого выделим ячейки G29:G30 (рис. 4.3), нажмем кнопку КОПИРОВАТЬ. Выделим ячейку D48 (рис. 4.4) и вызовем команду ПРАВКА – СПЕЦИАЛЬНАЯ ВСТАВКА – ВСТАВИТЬ «Значения» – ОК. Проделываем аналогичную процедуру для других значений: выделить G31:G34 – КОПИРОВАТЬ – Курсор в ячейку E46 – ПРАВКА – СПЕЦИАЛЬНАЯ ВСТАВКА – ВСТАВИТЬ «Значения» – ОК и т.д. Таким образом, мы установили соответствие между оценками сезонных компонент, соответствующих определенному кварталу.

Найдем средние оценки сезонной компоненты для каждого квартала (по годам) 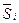при помощи встроенной статистической функции СРЗНАЧ. Например, H46 = СРЗНАЧ(D46:G46) и т.д.

Корректирующий коэффициент в ячейке H50 считается как среднее значение по всем 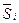. Для аддитивной модели скорректированные значения сезонной компоненты S_i рассчитаем как разность между средней оценкой 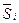и корректирующим коэффициентом. В нашем примере, I46 = H46 – H$50 и т.д. Для мультипликативной модели находим частное от деления средней оценки на корректирующий коэффициент.

Следует помнить, что в аддитивной модели сумма значений сезонных компонент S_i должна быть равна нулю, в мультипликативной – числу периодов в цикле. Для нашего примера длина цикла равна 4 квартала.

Шаг 3. Устранить сезонную компоненту из исходных уровней ряда. Построить уравнение, моделирующее динамику трендовой компоненты.

Составим рабочую таблицу (рис. 4.5). Скопируем статистические данные в ячейки D54:D69. Столбец сезонных компонент S_t сформируем при помощи команды СПЕЦИАЛЬНАЯ ВСТАВКА. В следующем столбце таблицы рассчитаем выровненные значения ряда: для аддитивной модели 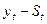, для мультипликативной модели 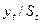. Мы получили ряд, в котором отсутствует сезонная компонента.

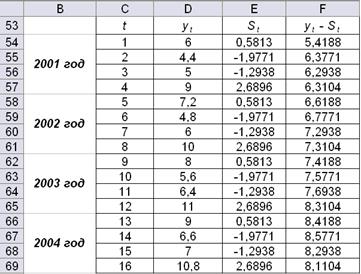
Рис. 4.5. Устранение сезонных компонент из уровней ряда

Построим уравнение линейной регрессии, в котором в качестве независимого фактора выступает время t. Получим линейное уравнение вида: 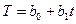, где T – значение трендовой компоненты, t – номер наблюдения. Используем команду СЕРВИС – АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ (см. рис 4.6). В меню РЕГРЕССИЯ обязательно отметим Остатки, чтобы оценить наличие автокорреляции в остатках.

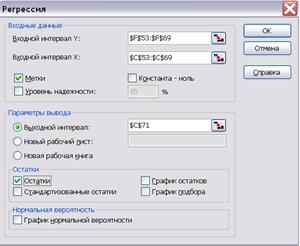
Рис. 4.6. Использование команды РЕГРЕССИЯ

для нахождения трендовой компоненты уровней ряда

Для рассматриваемого примера получим числовые данные, представленные на рис. 4.7.

Рис. 4.7. Протокол выполнения регрессионного анализа

Оценим качество полученного уравнения по коэффициенту корреляции, детерминации, t -статистикам, F -статистике (см. приложение 1 и приложение 2). Обратим внимание, что в ячейках D93:D108 находятся расчетные значения трендовой компоненты T для каждого наблюдения, а в ячейках E93:E108 – остатки (см. рис. 4.7).

Рассчитаем значение коэффициента Дарбина-Уотсона (см. рис. 4.8). Статистику Дарбина – Уотсона найдем по формуле:

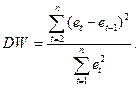(4.1)

В ячейке F109 найдем значение числителя, а в ячейке E109 – значение знаменателя, здесь использована математическая функция СУММКВ, которая возвращает значение суммы квадратов заданного массива (см. рис. 4.8).

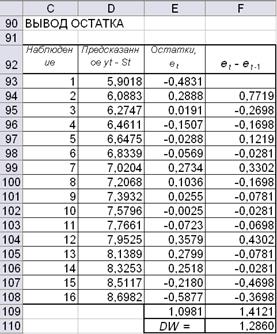
Рис. 4.8. Расчет коэффициента Дарбина-Уотсона

Для рассматриваемого примера все статистики оказались удовлетворительными, кроме статистики Дарбина-Уотсона. DW = 1,286, причем d_L = 1,1 < 1,286 < 1,37 = d_U для 16 наблюдений и 1 независимой переменной t. Значения d_L и d_U статистик Дарбина-Уотсона при 5%-ном уровне значимости см. в приложении 3. Таким образом, невозможно определить, присутствует ли автокорреляция в остатках построенной модели. На практике в этом случае предполагают наличие автокорреляции в остатках. Возможно, выбрав нелинейную форму тренда, мы сможем избавиться от автокорреляции.

Шаг 4. Рассчитать прогноз.

Рассчитаем прогноз объема потребления электроэнергии в 1 квартале 2005 года: 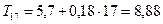, 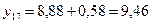. Таким образом, в 1 квартале 2005 года ожидается объем потребления электроэнергии в размере 9 млн. 460 тыс. кВт.

Шаг 5. Оформить отчет о проделанной работе.

План отчета:

1. Укажите фамилию, имя, название группы, номер варианта.

2. Запишите полученные значения сезонных компонент.

3. Запишите уравнение линейного тренда в виде

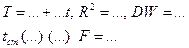
и оцените качество построенной модели по всем характеристикам. Особое внимание уделите критерию Дарбина-Уотсона. При наличии автокорреляции в остатках, попытайтесь объяснить причину.

4. Рассчитайте прогноз экономического показателя на ближайший временной промежуток, используя построенную модель.

ПРИЛОЖЕНИЯ

Приложение 1

Протокол регрессионного анализа.