Часть А. Выполните тестовые задания
1.Что называется эконометрикой?
а) метод применения математики в бухгалтерском учете;
б) наука, дающая количественное выражение взаимосвязей экономических явлений и процессов;
в) способ измерения взаимосвязей качественных процессов и явлений в экономике.
2.С какими науками связана эконометрика?
а) статистикой, экономической теорией, математикой;
б) бухгалтерский учет, статистика, экономика;
в) экономика, геометрия, алгебра.
3.Модель временных данных; регрессионная модель с одним уравнением; системы одновременных уравнений - это
а) этапы эконометрического моделирования;
б) виды переменных;
в) типы эконометрических моделей.
4.Случайная величина ɛ называется:
а) свободным членом;
б) возмущением;
в) оценкой уравнения.
5.Чем отличается парная регрессия от множественной:
а) количеством результативных признаков;
б) количеством факторных признаков;
в) характером расположения точек на корреляционном поле.
6.Что такое спецификация модели?
а) характеристика силы связи между переменными;
б) формулировка вида модели;
в) показатель измерения переменных.
7.Коэффициент регрессии –это:
а) параметр, являющийся сомножителем факторного признака;
б) величина, характеризующая тесноту связи между результативным и факторным признаком;
в) результативный признак.
8.Коэффициент детерминации –это:
а) параметр уравнения регрессии;
б) оценка качества подбора функции;
в) ошибка выборки.
9.При каком виде корреляционной связи коэффициент корреляции имеет знак минус?
а) криволинейной;
б) множественной;
в) обратной.
10.Какие выводы можно сделать о взаимодействии между результативными и факторными признаками, если для парной линейной зависимости получено значение коэффициента корреляции r = - 0,87:
|
|
а) связь сильная, прямая;
б) связь слабая, обратная;
в) связь сильная, обратная.
Часть Б. Задания на соответствие
- Установите соответствие
| 1. y = a + bx | А. парная нелинейная регрессия |
| 2. y = a+b1x+b2x2 | Б. парная линейная регрессия |
| 3. y = abx | В. множественная регрессия |
- Установите соответствие
| 1. Положительная корреляция | А. корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной |
| 2. Отрицательная корреляция | Б. корреляция, при которой увеличение одной переменной связано с увеличением другой переменной. |
- Установите соответствие
| 1. значение коэффициента корреляции близко к 1 | А. это означает наличие слабой связи между переменными |
| 2. значение коэффициента корреляции близко к 0 | Б. это означает наличие сильной связи между переменными. |
- Установите соответствие
| 1. коэффициент корреляции | А. показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных. |
| 2. коэффициент детерминации | Б. показывает тесноту статистической взаимосвязи двух или нескольких случайных величин |
- Установите соответствие между наименованиями элементов уравнения
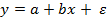и их буквенными обозначениями:
| 1. У | А. случайные отклонения |
| 2. Х | Б. параметры регрессии |
| 3. а, b | В. объясняющая переменная |
| 4. ɛ | Г. объясняемая переменная |
Часть В. Решите задачу
- По имеющимся данным сформулировать априорные предположения о возможной связи между факторами, определив зависимую и независимую переменные.
- Рассчитать оценки парной линейной регрессионной модели по методу наименьших квадратов (МНК).
- Дать интерпретацию коэффициентам регрессии.
- Рассчитать парный линейный коэффициент корреляции и дать интерпретацию.
- Оценить статистическую значимость коэффициентов регрессии и корреляции, приняв уровень значимости 95%.
- Рассчитать теоретический коэффициент эластичности и дать ему интерпретацию.
Имеются данные по 10 фермерским хозяйствам области:
|
|
| N п/п | ||||||||||
| Урожайность зерновых, ц/га | ||||||||||
| Внесено удобрений на 1 га посева, кг | 3,9 | 2,4 | 5,1 | 5,9 | 7,3 | 5,7 | 6,9 | 3,4 | 7,0 | 3,0 |
Типовые задачи.
Тема 1.
- Построить линейное уравнение парной регрессии y от x.
- Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
- Оценить статистическую значимость параметров регрессии и корреляции с помощью F -критерия Фишера и t -критерия Стьюдента.
- Выполнить прогноз y при прогнозном значении x, составляющем 107% от среднего уровня.
- Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
- На одном графике построить исходные данные и теоретическую прямую, интерпретировать полученные данные.
Тема 2.
1. Найти уравнение степенной регрессии y = axb.
2. Привести уравнение к линейному виду.
3. Найти нелинейный коэффициент парной корреляции и с доверительной вероятностью p = 0,9 проверить его значимость.
4. Найти линейный коэффициент парной корреляции и с доверительной вероятностью p = 0,9 проверить его значимость. Интерпретировать полученные данные.
|
|
5. Найти уравнение регрессии вида y=ax2+bx+c.
6. Найти нелинейный коэффициент парной корреляции
7. Проверить с доверительной вероятностью p=0,95 значимость коэффициента корреляции. Интерпретировать полученные данные.
Тема 3.
1. В соответствии с методом наименьших квадратов найти уравнение множественной регрессии.
2. Найти парные коэффициенты корреляции.
3. Найти множественный коэффициент корреляции.
4. Найти скорректированный коэффициент множественной детерминации.
5. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента корреляции.
6. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
7. Осуществить отбор факторов, составить уравнение парной линейной регрессии. Интерпретировать полученные данные.
Тема 4.
1. Найти уравнение парной регрессии Y на Х и оценить его значимость;
2. Введя фиктивную переменную, найти уравнение множественной регрессии по всем объясняющим переменным;
3. Проследить за изменением скорректированного коэффициента детерминации при переходе от парной к множественной регрессии;
4. Оценить на уровне значимости 0.05 значимость различия между свободными членами уравнений, получаемых из общего уравнения множественной регрессии Y для каждой области. Интерпретировать полученные данные.
Тема 5.
1. Найти коэффициенты автокорреляции со смещением на 1, 2, 3, 4 месяца.
2. Проверить найденные коэффициенты на значимость при уровне значимости 0,05.
3. Построить коррелограмму.
4. Построить модель тенденции временного ряда. Интерпретировать полученные данные.
3.2.4 Типовые вопросы для подготовки к экзамену
1. Этапы построения эконометрических моделей
2. Парная линейная регрессия
3. Метод наименьших квадратов
4. Коэффициент парной линейной корреляции
5. Парная нелинейная регрессия. Оценка параметров
6. Оценка существенности (значимости) параметров уравнения регрессии
7. Интервалы прогноза по линейному уравнению регрессии. Построение доверительных интервалов
8. Нелинейная регрессия. Виды нелинейных уравнений парной регрессии
9. Множественная регрессия. Отбор факторов при построении множественной регрессии
10. Матрица парных коэффициентов корреляции.
11. Коллинеарность. Мультиколлинеарность
12. Оценка параметров уравнения множественной регрессии
13. Уравнение множественной регрессии в стандартизованном масштабе. Оценка коэффициентов Bi
14. Переход от уравнения множественной регрессии в натуральном масштабе к уравнению в стандартизованном масштабе и обратно
15. Частные уравнения регрессии
16. Множественная корреляция
17. Частные коэффициенты корреляции
18. Оценка надежности результатов множественной регрессии и корреляции. Частный Fxi
19. Фиктивные переменные в уравнении множественной регрессии
20. Система одновременных уравнений. Структурная и приведенная форма модели
21. Временные ряды.
22. Автокорреляция во временных рядах
23. Построение линейного тренда
Методические материалы, определяющие процедуры оценивания знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций, формируемых в ходе освоения данной дисциплины