Механизмы упругой поляризации.

Представление диэлектриков с помощью эквивалентных

 

5.1. Релаксационный спектр, соответствующий RLC−цепям

Релаксационный спектр, соответствующий RL−цепям, может возникать в магнитных материалах, и, наконец, могут проявиться резонансные спектры, которые отличаются от релаксационных наличием аномальной дисперсии диэлектрической проницаемости.

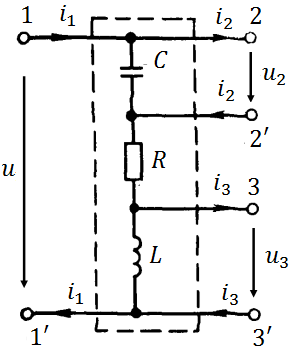
Рассмотрим частотную зависимость последовательной – цепи (рис. 4.8).

 

а	б
Рис. 4.8. К определению входных и передаточных характеристик последовательного колебательного контура [14]

 

Приложенное синусоидальное напряжение уравновешивается напряжением на трех элементах цепи, т.е. можно записать

 

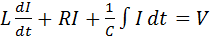(4.17)

Решение этого дифференциального уравнения для установившегося режима синусоидальных токов равно

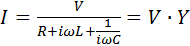(4.18)

ВХОДНЫЕ ХАРАКТЕРИСТИКИ

При исследовании комплексных частотных характеристик последовательный колебательный контур удобно представлять в виде многополюсника с тремя парами выводов (рис. 4.8, а, б).Внешнее воздействие на контур обычно задают в виде напряжения 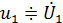приложенного к зажимам 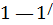, а в качестве отклика цепи рассматривают входной ток цепи 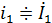напряжение на емкости 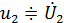или напряжение на индуктивности . Таким образом, последовательный колебательный контур обладает как входными, так и передаточными характеристиками.

Рассмотрим АЧХ и ФЧХ входной проводимости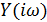

 

Для 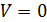дифференциальное уравнение (4.17) преобразуется в уравнение переходного процесса последовательной резонансной цепи. Заменяя ток зарядом конденсатора, можно записать

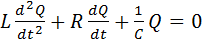(4.31)

Принимая решение в виде

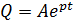(4.32)

и подставляя его в уравнение (4.31), находим, что р должно удовлетворять условию

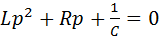(4.33)

Отсюда

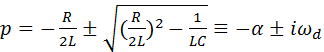(4.34)

Свободно колеблющаяся цепь RLC имеет коэффициент затухания

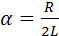(4.35)

и частоту

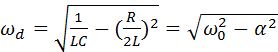(4.36)

которая для цепи без затухания идентична резонансной частоте установившегося состояния. Введя α и ω₀ в решение уравнения (4.34), получим полную проводимость резонансной цепи в виде

(4.37)

В случае слабого затухания (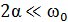) удобно иметь дело не с самой частотой, а с ее отклонением от резонансного значения путем приближения

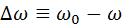(4.38)

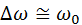(4.39)

(4.40)

Приравнивая выражения (4.2) и (4.40), получим относительную диэлектрическую проницаемость, коэффициент потерь и тангенс угла потерь резонирующего диэлектрика (рис. 4.14) [10, 14]:

 

Сведение проводимости к параллельной схеме замещения по формулам, выведенным ранее:

Параллельное соединение
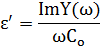
	(4.2,а)
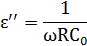
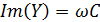
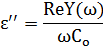
	(4.2,б)
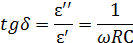
	(4.3)

 

Вывод для :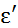

 

В итог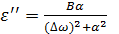е

( где 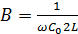)	(4.41)

 

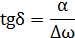
Диэлектрическая проницаемость 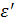возрастает с частотой, достигая максимума, равного , при 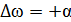, затем падает, проходя через нуль при резонансной частоте, до минимума, равного , при 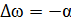, и вновь асимптотически приближается к нулю. Эта аномальная дисперсная характеристика диэлектрической проницаемости типична для резонансного спектра. Она сопровождается колоколообразной характеристикой поглощения 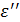, которая при ω₀ проходит через максимум, равный 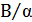. Фазовый угол δ изменяется от нуля при низкой частоте до 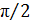при резонансе и 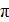при высокой частоте, проходя через значения 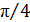и в точках .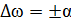

Мощность, отданная резонансной цепи источником синусоидального напряжения постоянной амплитуды, изменяется пропорционально 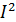, т.е.

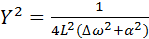(4.42)

Точки 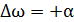являются точками половинной мощности последовательной резонансной цепи с низким затуханием [см. уравнение 4.9], т.е.

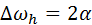(4.43)

является половиной ширины резонансной кривой поглощения. Относительная половина ширины, равная

(4.44)

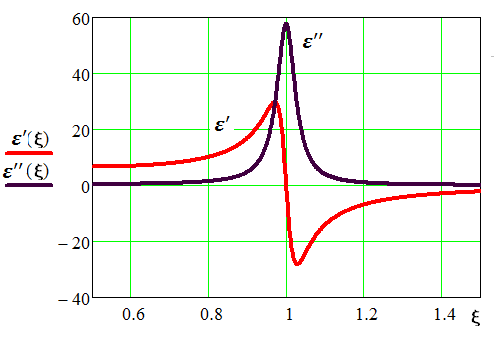
Рис.4.14. Резонансные характеристики диэлектрика 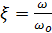[10]

 

Если элементы резонансной цепи с сосредоточенными параметрами включаются параллельно питающему напряжению (рис.4.15), то полное сопротивление (а не полная проводимость) становится максимальным при резонансе

Рис. 4.15. Параллельный резонансный контур[10].

 

и ток, получаемый от источника постоянного напряжения, проходит через минимум при ω₀. Это положение соответствует поведению диэлектрика или передающей линии, настроенной на антирезонанс.

С введением таких эквивалентных схем, симулирующих свойства диэлектриков, завершается задача макроскопической теории. Более глубокое исследование поведения диэлектриков уводит нас от феноменологической теории к молекулярной.

 

Механизмы упругой поляризации.

По существу мы будем обсуждать решеточные колебания (колебания атомов в кристаллической решетке, приводящие к атомной поляризации) в диэлектриках и полупроводниках. Можно утверждать, что колебания атомов в кристалле могут быть описаны волновыми уравнениями. Например, звук является такого рода колебанием. Таким образом, движения атомов в кристалле могут быть охарактеризованы их векторами смещений (в реальном пространстве) и их волновыми векторами k.

Длинноволновое колебание в кристалле заключается в почти однородном смещении идентичных атомов в различных элементарных ячейках, такие колебания называются акустическими.

Колебания атомов или ионов под воздействием внешнего переменного электрического поля при атомной поляризации в кристаллах, содержащих более одного атома в примитивной ячейке, можно разделялись на акустические и оптические фононы, по аналогии с фотонами при распространении световых волн. Как следует из названия, оптические фононы могут взаимодействовать с электромагнитным излучением

Поскольку фононы представляют собой квантованные простые гармонические осцилляторы, начнем с рассмотрения отклика совокупности идентичных заряженных простых гармонических осцилляторов (ПГО) на поле излучения в виде плоской волны [5]:

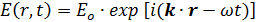, (3.77)

Предположим, что эти ПГО равномерно распределены по всему пространству (во избежание проблем, связанных с анизотропией или наличием поверхностей). Массу и заряд ПГО обозначим М и Q, соответственно. Естественной колебательной частотой каждого из них является . Под действием приложенного поля ПГО смещаются из своего положения равновесия на вектор 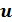. Уравнение их движения имеет вид

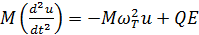(3.78)

В равновесном состоянии решения (3.78) могут быть выражены как:

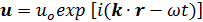(3.79)

Подставляя последнее выражение в (3.78), получим решение для :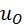

(3.80)

Поскольку эти ПГО заряжены и смещаются на одинаковую величину 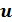, они создают макроскопическую поляризацию , которая также колеблется c частотой :

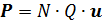, (3.81)

где − плотность ПГО. Вектор электрического смещения 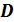среды выражается в системе единиц СИ как

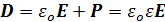, (3.82)

где 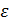− диэлектрическая функция изотропной среды. Подставив (3.80) и (3.81) в (3.82), найдем ε в СИ [5]:

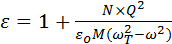. (3.83)

Прежде чем продолжить рассмотрение (3.83), необходимо включить в полную диэлектрическую функцию среды вклад от валентных электронов. Чтобы отличать вклад валентных электронов от вклада ПГО, обозначим эти вклады как 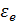и 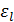(е и ℓ являются обозначениями электрона и решетки). Пусть ширина запрещенной зоны (низкая частота), так что для электронов поле излучения представляется постоянным и 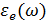можно аппроксимировать как 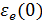. С другой стороны, если и 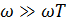, то ПГО не могут следовать за электрическим полем и больше не вносят вклада в полную диэлектрическую функцию, т.е. в (3.83) 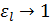. Таким образом, для полная диэлектрическая функция 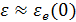. Принято обозначать 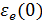как 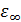и называть ее высокочастотной диэлектрической постоянной, поскольку это − диэлектрическая постоянная при частоте, которая много выше колебательных частот, но ниже энергий возбуждения электронов. Если включить 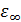в (3.83), то 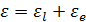в СИ будет иметь вид

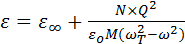, (3.84)

при условии, что .

Поскольку в среде нет избыточных зарядов, вектор электрического смещения D удовлетворяет уравнению Гаусса:

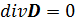(3.85)

Или эквивалентно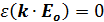

Случай 1 (поперечное поле): .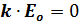

является резонансной частотой среды при возбуждении поперечного колебания (или сокращенно поперечной резонансной частотой).

Случай 2 (продольное поле): 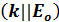и .

Если электрическое поле является продольным 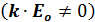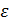должна обратиться в нуль, это может произойти при частотах 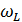определяемых из условия . (или сокращенно продольной резонансной частотой).

Заряд Q и масса М ПГО являются микроскопическими параметрами, которые трудно измерить. Напротив, , , 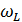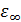можно определить из эксперимента. Часто бывает удобно ввести другую величину − так называемую низкочастотную диэлектрическую постоянную 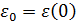, для того чтобы выразить диэлектрическую функцию через измеряемые величины [5]:

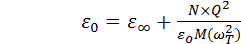, (3.86)

тогда

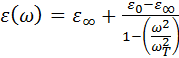(3.87)

или

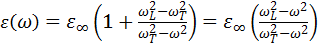(3.88)