ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

 

Литература: [1] §12.2; [3] §14; [4] §III.I; [5] §2.1; [12] §2.2

 

Задача 1.1 Для балок, схемы которых представлены на рис. 1.1, построить эпюры поперечных сил Q и изгибающих моментов М.

Исходные данные взять из таблицы 1.1

Таблица 1.1

№ строки	номер схемы	l1 м	l2 м	L3 м	М кНּм	Р кН	q кН/м
Вариант А	Вариант В
1						–
2							–
3						–
4							–
5						–
6							–
7						–
8							–
9						–
0							–
	е	е	е	г	д	д	д	е

Пример выполнения задачи 1.1. Для балки, представленной на рис. 1.2,а построить эпюры Q и M.

Решение. Определение опорных реакций.

Составим уравнения суммы моментов всех сил относительно опорной точки А (рис. 1.2,а).

, отсюда получим R_B=50кН.

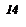
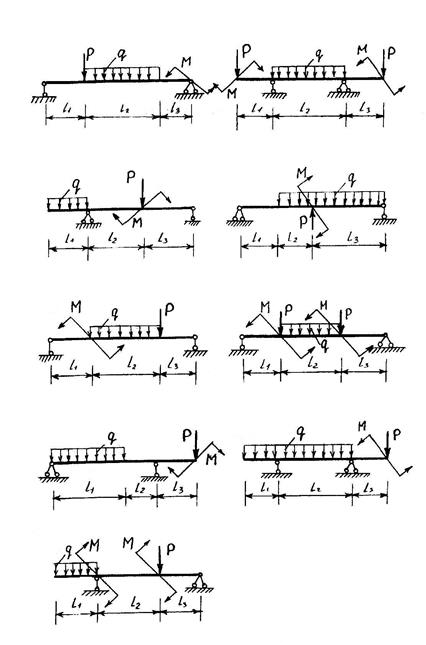
Из уравнения суммы моментов относительно точки В

 

 

определяем опорную реакцию R_А=30кН

Для проверки полученных реакций проецируем все силы на ось

 

.

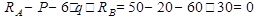Построение эпюр Q и M. Балка имеет пять грузовых участков.

Участок 1 (рис. 1.2, а, ). Проводим сечение 1-1.

Отбрасываем правую часть балки и рассматриваем равновесие левой части (рис. 1.2, б), т.к. для нее уравнения включают меньшее число слагаемых.

, отсюда определяем

;

Из уравнения

находим .

Участок 2 (рис. 1.2, а), . Проводим сечение 2-2 и рассматриваем равновесие левой части балки (рис. 1.2,б). Из уравнения равновесия определяем Q₂ и M₂:

;

 

Участок 3 (рис. 1.2, а, ). Рассматриваем равновесие части балки, расположенной правее сечения 3-3 (рис. 1.2, б).

Запишем уравнение для М₃ и Q₃:

; .

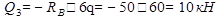Участок 4 (рис. 1.2,а, ). Для определения М₄ и Q₄ рассматриваем равновесие части балки, расположенной правее сечения 4-4:

.

 

 

Для определения положения сечения, где момент М₄ принимает экстремальное значение, приравняем поперечную силу Q₄ к нулю

Q₄=0; ; x ₄=3м.

Подставляя значение X₄ в уравнение М₄, находим

.

Участок 5 (рис. 1.2,а, ). Рассмотрим равновесие части консоли (рис. 1.2, б) и запишем выражения для М₅ и Q₅:

.

Эпюры Q и M для всей балки показаны на рис. 1.2, в, г.

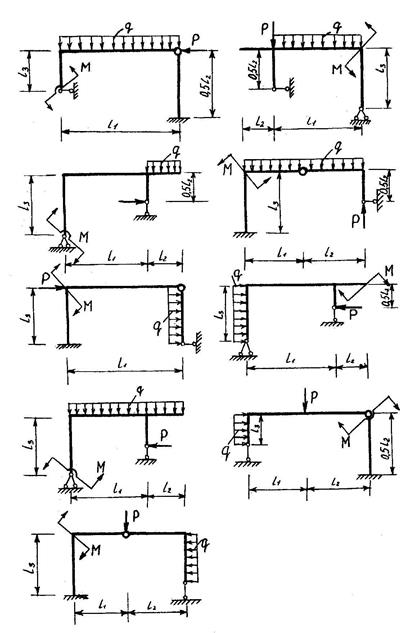
Задача 1.2. Для рам, схемы которых представлены на рис. 1.3, построить эпюры поперечных, продольных сил и изгибающих моментов. Исходные данные взять из таблицы 1.2.

Таблица 1.2

№ строки	номер схемы	l1 м	l2 м	l3 м	М кНּм	Р кН	q кН/м
Вариант А	Вариант В
1							–
2						–
3							–
4						–
5							–
6						–
7							–
8						–
9							–
0						–
	е	е	Е	г	д	д	Д	Е

 

Пример выполнения задачи 1.2. Для рамы, изображенной на рис.1.4,а, построить Q, M, и N.

Решение. Определение опорных реакций.

Для определения реакций R_A составим уравнение суммы моментов относительно шарнира С (рис. 1.4, а) для левой части рамы

 

; .

Получим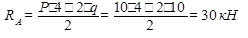

 

Реакции в защемлении В определим из уравнений равновесия, составленных для всей системы:

; ;

; ;

; .

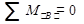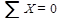Получим

 

;

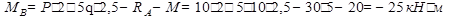Н_В=Р=10кН; R_B=5q-R_A=5ּ10-30=20 кН.

Проверка. Составим сумму моментов относительно точки А (рис. 1.4, а):

 

; .

Построение эпюр M, Q, N. При составлении уравнений для изгибающих моментов М₁ предполагаем внутренние волокна рамы растянутыми.

Участок 1 (рис.1.4, а, 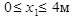). Запишем уравнения для М₁, Q₁, и N₁ , действующих на участке АК (рис. 1.4, б):

 

; ; .

 

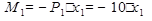Знак "минус" перед выражением М₁ показывает, что на участке АК растянуты внешние волокна.

Участок 2 (рис. 1.4, а, ). Рассматриваем равновесие части рамы, расположенной левее сечения 2-2 (рис. 1.4, в).

Определяем M₂, Q₂ и N₂:

;

; .

 

На данном участке изгибающий момент изменяется по закону квадратной параболы. Для определения экстремальной величины M₂ найдем значение x₂, при котором Q₂ равно нулю

 

Q₂=0; 30-10x₂=0; x₂=3м;

подставляя в M₂ , находим

 

Участок 3 (рис. 1.4,а, ). Уравнения для определения M₃, Q₃ и N₃ удобнее записать для части рамы, расположенной ниже сечения 3-3 (рис. 1.4, г):

М₃=-М_В -Н_Вּx₃=25-10x₃;

Q₃=Н_В=10кН; N₃=-R_В=-20кН.

Исходя из составленных уравнений, строим эпюры M, Q и N (рис. 1.4, д, е, ж).

Выполним статические проверки построенных эпюр. Вырезаем узлы рамы и составляем уравнения суммы моментов для каждого из них (рис. 1.4, з, и):

ΣМ_К=М₂-М₁=40-40=0;

ΣМ_D=М₂+М₃-М=15+5-20=0.

Рассекая раму по стойкам, рассмотрим равновесие верхней части (рис. 1.4, к). Спроектируем все силы на оси x и y:

 

ΣX=N₁-5q+N₂=30-50+20=0;

ΣY=Q₁-Q₃=10-10=0.

 

Проверки показывают, что все расчеты выполнены правильно.

 

 

Контрольная работа №2