МПС РОССИИ
Государственное образовательное учреждение
Высшего профессионального образования
«Ростовский государственный университет путей сообщения
Министерства путей сообщения Российской Федерации»
(РГУПС)
Н.И. Гриненко, А.И. Кирюнин
РАСЧЕТ НАДЕЖНОСТИ
УСТРОЙСТВ АВТОМАТИКИ, ТЕЛЕМЕХАНИКИ
И СВЯЗИ
Методические указания
К практическим занятиям по дисциплине
«Основы теории надежности»
Ростов–на–Дону
УДК 656.256
Гриненко Н.И., Кирюнин А.И.
Расчет надежности устройств автоматики, телемеханики и связи: Методические указания к практическим занятиям по дисциплине: «Основы теории надежности». – Ростов н/Д: Рост. гос. ун–т путей сообщения, 2003. – 52 с.
Излагаются основные сведения теории надежности, приведены примеры решения задач по основным разделам теории, часть задач предлагается для самостоятельного решения.
Методические указания написаны в соответствии с учебной программой по дисциплине: «Основы теории надежности» и предназначены для студентов специальности 210700.
Одобрены к изданию кафедрой: «Автоматика и телемеханика на ж.д. транспорте» РГУПС.
Табл. 1. Ил. 18.
Рецензенты: канд. техн. наук, доц. А.И. Зотов (РГАСХМ);
канд. техн. наук, доц. В.Н. Соловьёв (РФ МГТУГА)
ã Ростовский государственный университет
путей сообщения, 2003
Практическое занятие № 1
Тема занятия: Вычисление количественных
Характеристик надежности
Невосстанавливаемых систем
Цель занятия
1.1. Получить и закрепить необходимые теоретические сведения по характеристикам надежности невосстанавливаемых систем.
|
|
1.2. Получить практические навыки в решении задач по вычислению количественных характеристик (показателей) надежности.
Теоретические основы
К числу показателей надежности невосстанавливаемых систем относятся:
1. Вероятность безотказной работы за время 
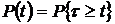, где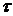 
–наработка до отказа; – требуемое время безотказной работы (или время, для которого определяется 
). Статистическое (приближенное) значение этой вероятности, определяемое по результатам опытных испытаний, равно
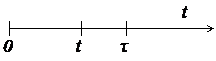
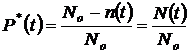
, (1.1)
где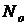 
– число однотипных объектов, поставленных на испытание;
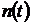– число отказавших объектов за время испытаний (за интервал времени (0, t));
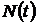– число не отказавших объектов за время t, 
.
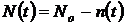Далее везде знак * будет обозначать статистическое значение соответствующих показателей надежности.
2. Вероятность отказа объекта за время 
.
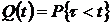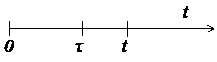
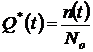, (1.2)
причем:
и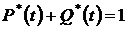 
. (1.3)
– является функцией распределения случайной величины 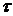(интегральным законом распределения случайной величины 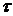или интегральным законом распределения отказов).
3. Плотность вероятности отказов 
(дифференциальная плотность (закон) распределения времени наработки до отказа 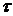, дифференциальная функция распределения случайной величины )
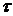. (1.4)
Из (1.4) имеем:
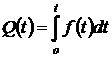, (1.5)
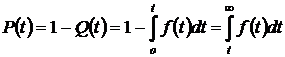, (1.6)
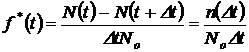1/ч, (1.7)
где 
– число отказавших объектов на интервале времени 
: от t до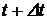 
.
Экспоненциальный закон распределения времени наработки до отказа 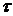(когда 
) определяется формулой
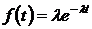. (1.8)
4. Интенсивность отказов:
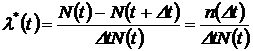1/ч, (1.9)
, (1.10)
, (1.11)
|
|
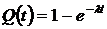, (1.12)
5. Средняя наработка до отказа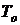 
.
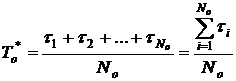, ч (1.13)
где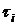 
– время наработки до отказа 
–го образца 
.
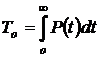. (1.14)
Порядок проведения занятия
3.1. Задачи №№ 1 
4 студенты решают поочередно у доски под руководством преподавателя.
3.2. Задачу № 5 студенты решают самостоятельно.
Содержание занятия
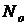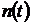Задача № 1. На испытание поставлено = 2000 однотипных изделий. За время = 4000 часов отказало = 100 изделий, а за последующие 
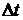= 100 часов отказало еще = 10 изделий. Определить статистические показатели надежности: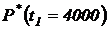 
, 
; 
; 
; 
; 
.
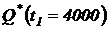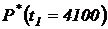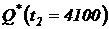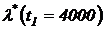Решение
1. По формулам (1.1) и (1.2) определяем вероятности безотказной работы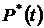 
и отказа 
за время испытаний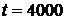 
час:
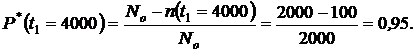
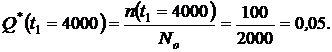
2. Определяем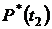 
и 
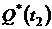за время испытаний 
:
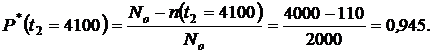
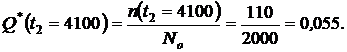
3. Определяем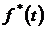 
за время 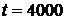час по формуле (1.7):
1/ч.
4. Определяем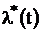 
за время 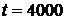по формуле (9):
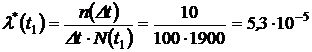1/ч.
Задача № 2. Производились испытания 4–х образцов однотипной аппаратуры. Наработка до отказа каждого из образцов составила, соответственно: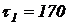 
час, 
ча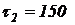с, 
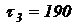час,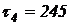 
час. Определить среднюю наработку до отказа 
Решение
Определяем 
по формуле (1.13):
час.
Задача № 3. Пусть в результате анализа данных об отказах невосстанавливаемой системы установлено, что плотность вероятности отказов распределена по закону:
Определить количественные показатели надежности и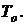 
Решение
1. Определяем вероятность безотказной работы по формуле (1.6):
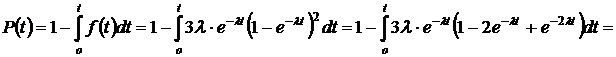
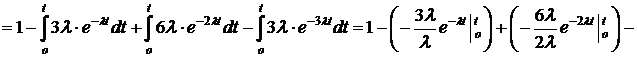
2. Определяем 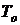по формуле (1.14):
.
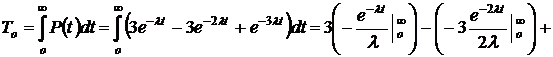
Задача № 4. Пусть время наработки до отказа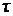 
системы телемеханики подчинено экспоненциальному закону 
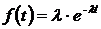с параметром 
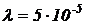1/ч требуется вычислить показатели надежности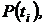 
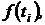
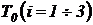для следующих значений времени: 
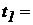250 час., 
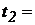500 час., 
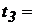1000 час.
|
|
Решение
1. Определяем вероятности безотказной работы системы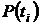 
:
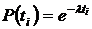
Примечание
Разложение в ряд Тейлора:
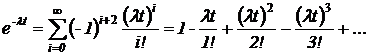
Если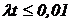 
, то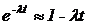 
.
Если 
, то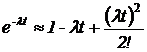 
.
,
,
.
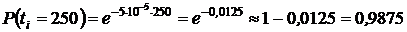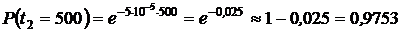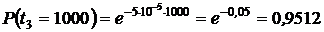Выводы:
1. С увеличением времени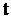 
вероятность безотказной работы 
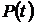уменьшается.
2. При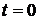 
, 
.
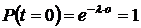3. При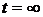 
, 
.
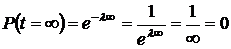2. Вычисляем 
:
,
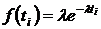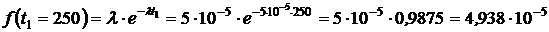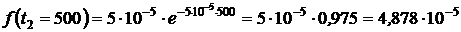1/ч,
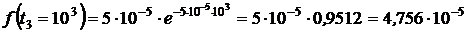1/ч,
1/ч.
Вывод. С увеличением времени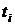 
величина уменьшается.
3. Вычисляем :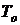
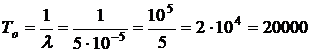ч.
Задача № 5. Плотность вероятности отказов системы имеет вид 
. Определить интенсивность отказов системы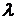 
и вероятность безотказной работы за время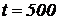 
час, если средняя, наработка системы до отказа равна 
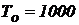час.
Подвести итоги занятия и выдать задания для самостоятельной работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основные понятия теории надежности: надежность, безотказность, ремонтнопригодность, долговечность, сохраняемость, отказ, виды отказов.
2. Количественные показатели надежности (безотказности) невосстанавливаемых систем:
– вероятности безотказной работы ,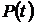 
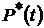и отказа 
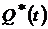. Графики функци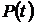й и ;
– плотность вероятности отказов , 
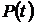. Связь вероятностей и с . Связь с 
;
– интенсивность отказов , 
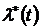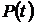. График функции . Связь с , и ;
– средняя наработка до отказа 
, . Связь показателя с вероятностью безотказной работы .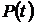
Записать и пояснить формулы для данных показателей безотказности и пояснить их физический смысл.
3. Расчет надежности невосстанавливаемых нерезервированных систем.