Пусть функция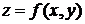 
непрерывна в некоторой замкнутой области. Тогда в силу второй теоремы Вейерштрасса функция достигает в этой области своего наибольшего и наименьшего значения. Это может происходить во внутренней точке 
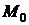, тогда для дифференцируемой функции 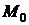– стационарная точка, которую находим с помощью необходимых условий экстремума. Если же своего наибольшего (наименьшего) значения функция достигает на границе области, то выражают, например, переменную 
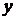из уравнения границы, подставляют в 
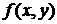и исследуют на экстремум полученную функцию одной переменной. Остаётся подсчитать значение функции во всех полученных точках и выбрать среди них наибольшее и наименьшее. Заметим, что при этом не надо проводить дополнительные исследования с помощью достаточного условия экстремума.
Пример 1. В области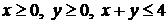 
найти наибольшее и наименьшее значение функции 
.
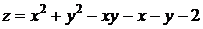Решение. Функция непрерывна и дифференцируема на всей плоскости.
1. Приравняем нулю частные производные:
. 
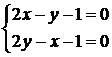
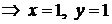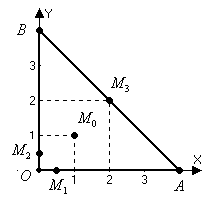
Получили единственную стационарную точку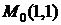 
, лежащую внутри заданной области. Значит, если функция 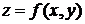внутри области имеет экстремум, то это возможно только в точке 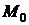. Подсчитаем 
.
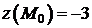2. Исследуем поведение функции на границе области.
а) На стороне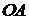 
: 
.
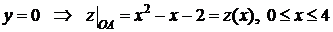Функция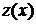 
непрерывна на 
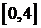, следовательно, достигает на этом промежутке наибольшего и наименьшего значения. Находим стационарную точку из условия 
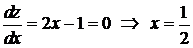. Значит, если функция 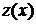внутри промежутка 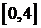имеет экстремум, то это возможно только при 
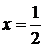. Этому значению на стороне 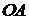соответствует точка 
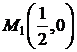. Подсчитаем 
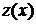. Осталось найти значения функции на концах промежутка : 
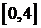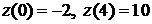. Это соответствует значениям функции 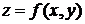в углах 
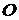и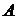 
: 
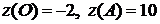
б) На стороне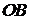 
: 
.
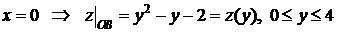Находим на 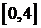стационарную точку из условия 
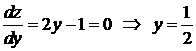. Этому значению на стороне 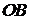соответствует точка 
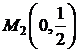. Подсчитаем 
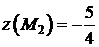. Осталось найти значения функции 
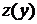на конце 
:: 
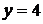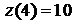. Это соответствует значению функции 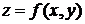в углу 
: 
.
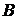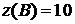в) На стороне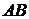 
: 
.
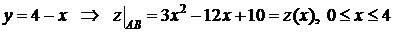Находим на 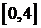стационарную точку: 
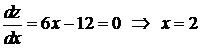. Этому значению на стороне 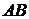соответствует точка 
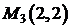. Подсчитаем 
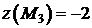. Значения функции в углах 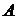и 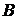уже найдены.
3. Выпишем значения функции в стационарных точках:
, 
,
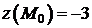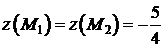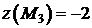
и значения функции в углах:
.
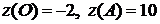
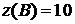Среди этих значений выбираем наибольшее и наименьшее:
, 
.☻
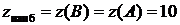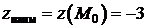Условный экстремум
Пусть в области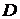 
задана функция 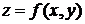. Точка 
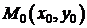называется точкой условного (относительного) экстремума функции 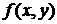, если
1) в этой точке достигается обычный экстремум,
2) ее координаты удовлетворяют уравнению связи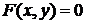 
.
При определении обычного экстремума значение функции в точке 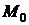сравнивается со всеми ее значениями в достаточно малой окрестности этой точки. А при определении условного экстремума из малой окрестности точки 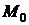выбираются только те точки, которые лежат на линии, определяемой уравнением связи.
Пример 1. Найти экстремум функции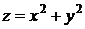 
при условии 
.
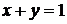Решение. Для решения этой задачи применим прямой метод. Выразим из уравнения связи одну переменную (например, ):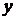
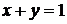
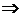
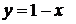
Подставим полученное выражение в заданную функцию:
.
Задача сведена к исследованию на обычный экстремум функции одной переменной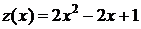 
. Решаем уравнение 
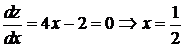– это точка минимума (так как 
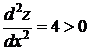). На линии 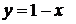этому значению соответствует точка 
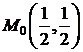. Геометрически это значит, что точка 
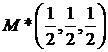, лежащая на параболоиде 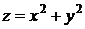и проектирующаяся в точку 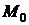, является самой низкой из всех точек параболоида, лежащих над прямой . ☻
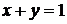Однако не всегда удается разрешить уравнение связи относительно одной из переменных (тем более что для большего числа переменных имеется система уравнений связи). В этих случаях применяют метод Лагранжа