Л А Б О Р А Т О Р Н А Я Р А Б О Т А 8

ИССЛЕДОВАНИЕ РЕЛЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ

 

Ц Е Л Ь Р А Б О Т Ы- исследование релейной системы автоматического регулирования второго порядка методом фазовой плоскости. В работе исследуются свободное движение системы, периодические режимы, способы стабилизации при различных характеристиках нелинейного элемента.

8.1. краткие сведения из теории

Релейные системы автоматического регулирования (САР) нашли широкое применение. Релейные САР являются важной разновидностью нелинейных систем. К релейным системам относятся системы с релейными усилителями и исполнительным устройством.

Отметим, что большое количество автопилотов, авторулевых для судов (поддержание заданного курса), систем регулирования температуры и различных следящих систем являются релейными.

Наряду с конструктивной простотой релейные системы обладают малым временем переходного процесса. Доказано, что во многих классах систем именно при применении релейной характеристики получается наименьшее время переходного процесса.

Система с одним релейным элементом всегда может быть представлена в виде одноконтурной схемы, содержащей релейный элемент и линейную часть (рис 8.1).

	Рисунок 8.1. Структурная схема нелинейной САУ.

 

Динамика такой САР будет описываться нелинейным дифференциальным уравнением. Хотя в общем случае нелинейных систем невозможно точное интегрирование нелинейного дифференциального уравнения, но в случае релейных систем можно получить точное решение. Дело в том, что в релейных системах нелинейная характеристика состоит из нескольких линейных участков. Пока входной сигнал реле находится в пределах одного из этих участков, движение системы описывается линейным дифференциальным уравнением.

В пределах другого линейного участка уравнение движения меняется. Движения на отдельных участках должны “припасовываться” друг к другу (по начальным и конечным условиям участков). Это “припасовывание” особенно легко осуществляется, когда линейная часть системы описывается дифференциальным уравнением второго порядка, если пользоваться понятием фазовой плоскости.

В общем случае нелинейное дифференциальное уравнение можно получить следующим образом. Согласно схеме рис.8.1 можно записать уравнение ошибки в изображениях по Лапласу:

, (8.1)

где

, (8.2)

. (8.3)

Тогда

, (8.4)

Для того, чтобы перейти к дифференциальным уравнениям, необходимо знать передаточную функцию линейной части. Так, в случае, когда

, (8.5)

получим следующее уравнение:

. (8.6)

В данной работе рассматривается автономная нелинейная система второго порядка с нелинейными дифференциальными уравнениями вида:

, . (8.6)

При заданных начальных условиях для величин x и скорости ее изменения в момент времени t = 0:

; (8.7)

получим однозначно определяемое решение уравнения (8.1), т.е. кривую x(t).

Значит, в случае систем второго порядка две величины x и v=dx/dt полностью определяют состояние системы в данный момент времени.

Плоскость, имеющая декартовыми координатами две переменные, полностью определяющие состояние системы, называются фазовой плоскостью. Под фазовой понимают состояние системы в какой-либо момент времени. Состояние системы второго порядка будет характеризоваться точкой на фазовой плоскости. Эта точка называется изображающей.

При движении системы происходит изменение ее состояния, т.е. изменяются фазовые координаты x и v. Поэтому изображающая точка системы будет при этом описывать некоторую траекторию, которая называется фазовой траекторией. Две фазовые траектории не пересекаются друг с другом (кроме особых точек). Поэтому из каждой точки фазовой плоскости исходит только одна траектория.

Совокупность фазовых траекторий, найденных для всевозможных начальных условий и так называемых особых точек и траекторий, составляет фазовый портрет системы.

Чтобы перейти к изображению процессов на фазовой плоскости, заменим предварительно уравнение (8.6) двумя уравнениями первого порядка:

(8.8)

В общем случае нелинейного уравнения второго порядка (8.6) уравнения (6.8) принимают вид:

(8.9)

В рассматриваемом частном случае R(x,v) = v, F(x,v) = -F(x). Исключив время t из уравнения (8.9), получим:

. (8.10)

Как легко видеть, это уравнение определяет направление фазовой траектории в любой не особой точке.

В особых точка, когда F(x,v) = 0 и R(v,x) = 0, значение dv/dx становится неопределенным, т.е. не существует определенного направления касательной к траектории в данной точке. Нетрудно видеть, что особым точкам соответствует состояние равновесия. Состояние равновесия, а значит, и особые точки, могут быть устойчивыми или не устойчивыми. Существуют шесть типов особых точек: центр, устойчивый фокус, неустойчивый фокус, устойчивый узел и особая точка типа ”седло”.

В нелинейной системе, в отличие от линейной, тип особой точки не всегда определяет поведение изображающей точки на всей фазовой плоскости. Фазовые траектории нелинейной системы могут иметь разный вид в различных областях фазовой плоскости. Фазовый портрет нелинейной системы может содержать:

- особые точки;

- сепаратрисы - особые траектории, разделяющие области с траекториями разного типа;

- предельные циклы - особые траектории, представляющие собой изолированные замкнутые фазовые траектории.

Наибольшее практическое значение имеет изучение систем, содержащих особые точки и предельные циклы. К числу таких систем относятся простейшие релейные системы второго порядка.

В лабораторной работе исследуется система, представленная на рис 8.2. В качестве релейного элемента рассматриваются идеальное реле и реле с гистерезисом.

Рисунок 8.2. Структурная схема релейной САУ и характеристики нелинейного элемента.

 

 

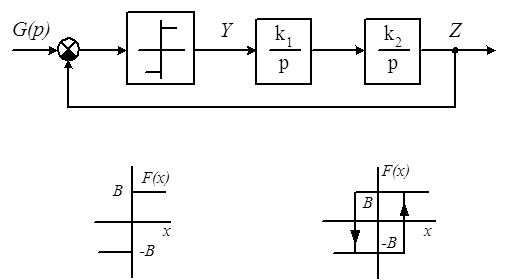
Угловым точкам характеристики реле соответствуют на фазовой плоскости так называемые линии переключения. Линии переключения делят фазовую плоскость на ряд областей, каждой из которых соответствует свое дифференциальное уравнение. При пересечении линии переключения некоторые из коэффициентов скачками меняют свои значения. Так, в случае системы с идеальным реле, линией переключения служит линия x = 0, т.е. ось v.

В этом случае F(x) = B при x > 0 и F(x) = -B при x < 0. Где В и -В входное напряжение реле. С учетом этого и принимая во внимание отрицательную обратную связь в САР, уравнение (8.10) будет иметь вид:

, (8.11)

, . (8.12)

Решив уравнения (6.11) и (6.12), получаем уравнение фазовых траекторий (параболы) вида:

, , (8.13)

, , (8.14)

где x₀ и v₀ - произвольные начальные значения переменных x и v.

Оказывается, в этом случае фазовые траектории системы представляют собой замкнутые кривые и имеется одна особая точка типа “центр”. Следовательно, в системе будет иметь место незатухающий периодический процесс.

В случае реле с гистерезисом аналогичные рассуждения показывают, что в системе положение равновесия не достигается, процесс будет расходиться. Это является следствием того, что гистерезис как бы вносит запаздывание при переключениях по сравнению с идеальным реле.

Естественно, что процессы в системе, как в случае идеального реле, так и в случае реле с гистерезисом, не могут быть признаны удовлетворительны. Поэтому возникает задача стабилизации релейных систем, которую можно производить двумя способами:

а) введением сигнала производной регулируемой величины - коррекция по скорости (рис.8.3, а);

б) введением демпфирования (рис.8.3, б).

Рисунок 8.3. Способы коррекции релейных систем.

 

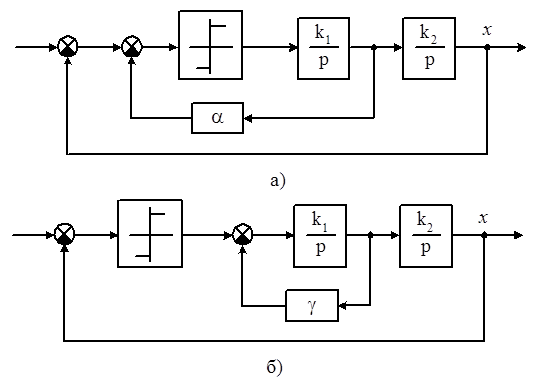
Анализируя фазовый портрет релейной САР с идеальным реле, легко прийти к выводу, что движение системы было бы устойчивым, если бы переключение фазовых траекторий осуществлялось не на линии х = 0, а несколько раньше, например, на прямой линии, лежащей во второй и четвертой четвертях и проходящей через начало координат. Этого можно добиться, если ввести в САР местную обратную связь по скорости (рис. 8.3, а). В этом случае переключение реле будет происходить при значении входного сигнала реле:

. (8.15)

Уравнение линии переключения, следовательно, имеет вид:

. (8.16)

Рассмотрим теперь второй способ - введение демпфирования. В этом случае одно интегрирующее звено охватывается жесткой обратной связью (рис. 8.3, б). Нетрудно показать, что нелинейное дифференциальное уравнение принимает вид:

. (8.17)

Появление в дифференциальном уравнении члена, пропорционального первой производной, свидетельствует о наличии затухания в системе.

Уравнение фазовых траекторий принимает вид:

. (8.18)

В случае введения демпфирования в систему с идеальным реле линией переключения будет линия х = 0, но изменяется вид фазовых траекторий. При этом процессы будут затухать - система становится устойчивой. Появляется одна особая точка - устойчивый фокус.

В случае реле с гистерезисом имеет место один устойчивый предельный цикл. Соответствующий выбор корректирующей цепи позволяет резко понизить амплитуду автоколебаний и увеличить частоту. Зная фазовую траекторию, можно построить процессы во времени методом Франка (метод равнобедренных треугольников). Для количественного анализа процесса в релейной системе второго порядка можно применить метод точечных преобразований.

	Рисунок 8.4. Схема модели для исследования релейных САУ методом фазовой плоскости.
	Рисунок 8.5. Модели применяемых нелинейных элементов и установка параметров реле с гистерезисом.

 

 

 

8.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Собрать схему исследования САУ с нелинейным элементом НЭ типа “идеальное реле” (рис. 8.4) без пунктирных связей. Модель “идеального реле” расположена в библиотеке Nonlinear и имеет вид, представленный на рис. 8.5. Коэффициент передачи установить k = 0,5.

* Для вывода фазовой траектории используются команды:

figure(1), plot(x, v), grid on, zoom on

* Для вывода кривой переходного процесса используются команды:

figure(2), plot(t, x), grid on, zoom on

2. Наблюдать фазовые траектории и соответствующие им переходные процессы при следующих начальных условиях:

а) х₀ = 5, v₀ = 0; t_мод = 30 с.

б) х₀ = 2, v₀ = 0; t_мод = 30 с.

в) х₀ = 0, v₀ = 2; t_мод = 30 с.

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

3. Ввести обратную связь по цепи a. Наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) a = 0.5, х₀ = 5, v₀ = 0, t_мод = 20 с;

б) a = 0.3, х₀ = 5, v₀ = 0, t_мод = 33 с.

По фазовой траектории, снятой экспериментально, вычислить значение коэффициента a. Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

4. Ввести обратную связь по цепи . Наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) = 0.5, х₀ = 5, v₀ = 0, t_мод = 18 с;

б) = 0.3, х₀ = 5, v₀ = 0, t_мод = 25 с.

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

5. Выполнить исследование нелинейной системы с гистерезисом. Для этого в схему исследований (рис. 8.4) без пунктирных связей вводится нелинейный элемент “реле с гистерезисом” с параметрами, приведенными на рис. 8.5. Наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) х₀ = 5, v₀ = 0, t_мод = 46 с;

б) х₀ = 2, v₀ = 0, t_мод = 36 с.

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

6. Ввести обратную связь по цепи a. Наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) a = 0.8, х₀ = 5, v₀ = 0, t_мод = 34 с;

б) a = 0.5, х₀ = 5, v₀ = 0, t_мод = 46 с.

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

7. Ввести обратную связь по цепи . Наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) = 0.1, х₀ = 5, v₀ = 0, t_мод = 32 с;

б) = 0.3, х₀ = 5, v₀ = 0, t_мод = 30 с.

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

8. Определить параметры автоколебаний в нелинейной системе с гистерезисом. Для этого наблюдать фазовые траектории и соответствующие им переходные процессы при:

а) = 0.4, х₀ = 5, v₀ = 0, t_мод = 35 с;

б) = 0.4, х₀ = 1, v₀ = 0, t_мод = 30 с.

в) a = 0.36, х₀ = 5, v₀ = 0, t_мод = 45 с;

Полученные графики фазовых траекторий и переходных процессов необходимо представить в отчете.

9. Рассчитать и построить фазовые траектории, соответствующие системе пунктов 2,а; 3,а; 4,а; 5,а; 6,а; 7,а.

8.3. СОДЕРЖАНИЕ ОТЧЕТА

В отчете о лабораторной работе необходимо привести:

1. Название и цель проведения лабораторной работы.

2. Схему модели релейной САР и схему исследований.

3. Характеристики релейных элементов.

4. Графики фазовых траекторий и соответствующие им графики переходных процессов, а также необходимые расчеты и построения по всем пунктам порядка выполнения работы.

5. Выводы по лабораторной работе.