ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Ц Е Л Ь Р А Б О Т Ы– определение передаточных функций разомкнутых и замкнутых линейных дискретных систем, исследование переходных процессов и устойчивости линейных дискретных систем.
10.1. краткие сведения из теории
Системы автоматического управления, в которых есть хотя бы один элемент дискретного действия, называются дискретными или импульсными САУ.
Любая дискретная система может быть приведена к схеме, состоящей из последовательно соединенных импульсного (дискретного) элемента ИЭ и непрерывной части НЧ системы (рис. 10.1,а).
|
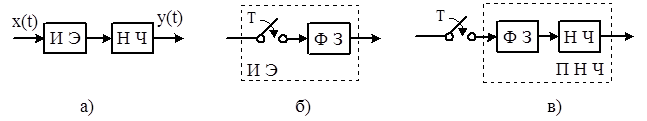
Математический аппарат для исследования дискретных систем предполагает, что выходной сигнал импульсного элемента представляет собой последовательность идеальных импульсов. Но реальный импульсный элемент формирует импульсы определенной длительности. Поэтому реальный импульсный элемент представляют эквивалентной схемой в виде последовательного соединения идеального импульсного элемента и формирующего звена ФЗ. Идеальный импульсный элемент формирует на выходе последовательность идеальных импульсов. Формирующее звено ФЗ преобразует идеальные импульсы в импульсы, по всем характеристикам не отличающиеся от импульсов на выходе реального импульсного элемента. Идеальный импульсный элемент на схемах обозначается в виде ключа (рис. 10.1,б).
Формирующее звено является линейным непрерывным элементом схемы и его относят к непрерывной части системы (НЧ) и эту часть системы называют приведенной непрерывной частью системы (ПНЧ). Таким образом, расчетная модель дискретной системы в разомкнутом состоянии представляет собой схему, состоящую из последовательного соединения идеального импульсного элемента и приведенной непрерывной части системы (рис. 10.1,в).
В модели линейной системы с амплитудно-импульсной модуляцией формирующее звено преобразует последовательность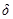 
- функций в последовательность прямоугольных импульсов, т.е. прямоугольный импульс является реакцией формирующего звена на воздействие в виде 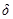- функции. Таким образом, реакция формирующего звена на 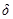- функцию представляет собой весовую функцию 
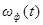. Как известно, изображение по Лапласу весовой функции есть передаточная функция.
Передаточная функция формирующего звена, соответствующая прямоугольной форме импульсов, равна:
.
Формирующий элемент с такой передаточной функцией называется фиксатором (экстраполятором) нулевого порядка.
Для исследования дискретных систем широкое распространение получил аппарат z-преобразования. Z-преобразование связано с дискретным преобразованием Лапласа посредством подстановки: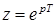 
.
Дискретной передаточной функцией называется отношение z-изображений выходной Y(z) и входной X(z) величин при нулевых начальных условиях. В практических задачах дискретную передаточную функцию определяют по передаточной функции непрерывной части используя таблицы соответствия между преобразованием Лапласа и z-преобразованием для временных функций.
Определим дискретную передаточную функцию системы, передаточная функция приведенной непрерывной части которой равна:
; 
.
;
.
Представим выражение 
в виде суммы простейших дробей:
Определим по таблицам z-преобразований:
; 
; 
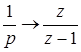, где 
.
где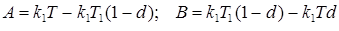 
.
Динамические свойства импульсных систем с амплитудной модуляцией во многом аналогичны динамическим свойствам непрерывных систем. Поэтому методы анализа таких импульсных систем являются аналогами соответствующих методов исследования непрерывных систем. Для суждения об устойчивости импульсных систем можно использовать обычные критерии устойчивости линейных систем, но при этом приходится учитывать лишь некоторые особенности импульсных систем. Так, для того чтобы применить критерий Гурвица, необходимо предварительно в характеристическом уравнении замкнутой дискретной системы
произвести замену переменной z на переменную 
путем подстановки
.
В результате подстановки получаем преобразованное характеристическое уравнение:
.
Исследование устойчивости по полученному преобразованному характеристическому уравнению производится в соответствии с критерием Гурвица для непрерывных систем.
Качество импульсных систем управления характеризуется такими же показателями, как и качество непрерывных систем: точностью в установившихся режимах, длительностью и перерегулированием переходного процесса.
Длительность и перерегулирование оценивают непосредственно по переходной характеристике. Переходная характеристика импульсной системы строится гораздо проще, чем для непрерывной системы. Для этого записывают z-изображение выходной величины при единичном ступенчатом воздействии
,
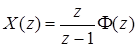а затем по изображению находят оригинал – решетчатую функцию x(iT).
В простых случаях функцию x(iT) можно найти при помощи таблиц обратного z-преобразования, разложив предварительно изображение X(z) на простые дроби.
В тех случаях, когда разложение на дроби связано с трудностями, целесообразно разложить функцию X(z) в степенной ряд по отрицательным степеням z (делением числителя на знаменатель):
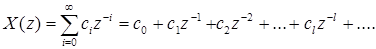
Из определения z-преобразования вытекает, что коэффициенты степенного ряда по степеням z-1 представляют собой значения переходной характеристики h(t) в дискретные моменты времени t = iT (i = 1; 2; 3;…), т.е.
…; 
…
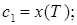
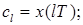10.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Собрать схему моделирования дискретной системы, которая приведена на рис. 10.1. Фиксатор нулевого порядка (Zero-Order Hold) (рис. 10.2) расположен в библиотеке Discrete. Единственный параметр этого блока – период дискретности Т.
2. Установить следующие параметры модели: Т1 = 1,5 с; Т = 0.1 с; k > 0.
3. Определить экспериментально граничное значение коэффициента передачи системы. Для этого необходимо, постепенно увеличивая значение коэффициента k, добиться незатухающих колебаний на выходе системы. График переходного процесса представить в отчете.
4. Изменяя значение k, получить три вида переходных процессов в системе: апериодический монотонный, апериодический c перерегулированием и затухающий колебательный. Для каждого вида переходного процесса указать значение k и представить в отчете графики переходных процессов.
5. Рассчитать граничное значение коэффициента передачи и сопоставить его с экспериментальным.
6. Исследовать влияние периода дискретности на качество управления и устойчивость в линейной дискретной системе. Для этого установить следующие параметры модели (рис. 10.2): Т1 = 1,5 с; k = 2.2.
7. Не изменяя значения Т1, k, получить переходные процессы при следующих значениях периода дискретности: Т = 0.01 с; Т = 0.1 с; Т = 0.5 с; Т =1 с. Для каждого переходного процесса указать значение Т и представить в отчете графики переходных процессов.
8. Выполнить аналитические расчеты устойчивости и переходных процессов в дискретной системе для приведенных значений периода дискретности.
|
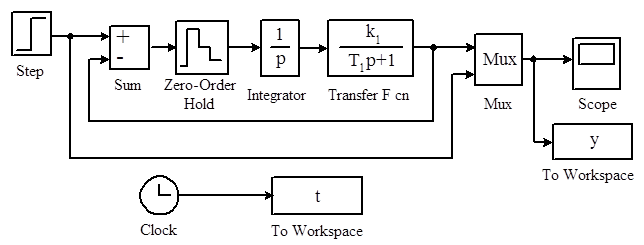
10.3. СОДЕРЖАНИЕ ОТЧЕТА
В отчете о лабораторной работе необходимо привести:
1. Название и цель лабораторной работы.
2. Схему модели линейной дискретной САУ.
3. Графики переходных процессов с указанием значений коэффициентов передачи k. Расчет kгр.
4. Графики переходных процессов с указанием значений периода дискретности Т.
5. Аналитические расчеты устойчивости системы при различных значениях периода дискретности.
6. Графики переходных процессов системы, рассчитанных аналитически для различных значений периода дискретности.
7. Выводы по лабораторной работе.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Лукас В.А. Теория автоматического управления: Учеб. для вузов. - 2-е изд., перераб. и доп.- М.: Недра, 1990. - 416 с.
2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования и управления. - М.: Наука, 1972. - 768 с.
3. Васильев Д.В., Чуич В.Г. Системы автоматического управления (примеры расчета). - М.: "Высшая школа", 1967. - 419 с.
4. Теория автоматического управления. Нелинейные системы / Под. ред. А.В. Нетушила. –2-е изд., перераб. и доп.- М. Высш. шк., 1983.- 432 с.
5. Цапенко Г.И., Борисов А.А. Дискретные автоматические системы. Текст лекций. Донецк, ДПИ, 1979.- 68 с.
6. Сборник задач по теории автоматического регулирования и управления. Под редакцией В.А. Бесекерского, издание пятое, переработанное, издательство "Наука", М., 1978. - 512 с.
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО КУРСУ
"ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ"
ЧАСТЬ II
(для студентов специальности 7.092501 АУП)
Составители:
ТКАЧЕНКО Валерий Николаевич
ПОПОВ Владислав Александрович
ФЕДЮН Роман Валериевич