Существуют различные способы определения функций Уолша. Рассмотрим способ, основанный на взаимосвязи функций Уолша с функциями Радемахера. Последние определяются так:
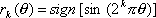
где 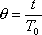 – безразмерное время (
– безразмерное время (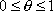 ), k є N – порядок (номер) функции,
), k є N – порядок (номер) функции,
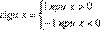
Система функций Радемахера ортонормированна на интервале (0,1), то есть
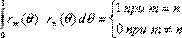
однако неполна.
Функции Уолша, образующие полную ортонормированную систему, теперь можно определить так:
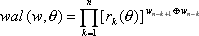
| (5) |
где «(+)» – сложение по модулю 2; w – порядок (номер) функции; n=log2 N, где N=2n – количество функций системы; wi – i-тый разряд двоичного представления порядка функции w (отсчёт слева, начиная с 0).
Функции Уолша могут служить базисом для спектрального представления сигнала, то есть любую интегрируемую на интервале  функцию можно представить рядом по системе функций Уолша:
функцию можно представить рядом по системе функций Уолша:
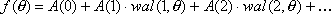
с коэффициентами
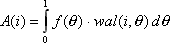
Способ нумерации функций в системе называется упорядочением. Функции Уолша, сформированные в соответствии с выражением (5), упорядочены по Уолшу. На практике также применяетсяупорядочение по Адамару (had(h,Эта)) и по Пэли (pal(p,Эта)).
Функции had(h,Эта) можно сформировать с помощью матрицы Адамара. Матрицей Адамара HN порядка N=2n, n є N называется квадратная матрица размера N x N с элементами +1 такая, что
HN x HNT = N x E,
где HNT – транспонированная матрица, E – единичная матрица; при этом H1=1.
Матрицу Адамара легко построить рекурсивно, так как:
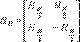
Функция Уолша, упорядоченная по Адамару (had(h,Эта)) с номером h, является последовательностью прямоугольных импульсов длительностью 1/N от интервала (0,1) с единичными амплитудами и полярностями, соответствующими знакам элементов h-той строки матрицы Адамара.
Для цифрового анализа сигнала используются дискретные функции Уолша, которые являются отсчётами соответствующих непрерывных функций. Каждый отсчёт расположен в середине связанного с ним элемента непрерывной функции длительностью 1/N от интервала (0,1). Дискретные функции Уолша, упорядоченные по Уолшу, можно определить так:
|
|
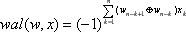
где xk – k-тый разряд в представлении номера отсчёта x в двоичной системе счисления:
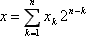
Другой формой представления дискретных функций Уолша является матрица Адамара, номера столбцов которой соответствуют номерам дискретных значений (отсчётов) функций Уолша, а номера строк – номерам функций Уолша.
Практическая реализация
На практике БПУ строится на основе ранее написанных процедур БПФ, в которых удаляется работа с мнимыми частями, переупорядочение перед рекурсивным вызовом и домножение на W при сборке.
22.
Сжатие без потерь (англ. Lossless data compression) — метод сжатия данных: видео, аудио, графики, документов представленных в цифровом виде, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.
Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.
Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы, такие как PNG, используют только сжатие без потерь; тогда как другие (TIFF, MNG) или GIF могут использовать сжатие как с потерями, так и без.
|
|
23.
Импульсно-кодовая модуляция (ИКМ, англ. Pulse Code Modulation, PCM) используется для оцифровкианалоговых сигналов. Практически все виды аналоговых данных (видео, голос, музыка, данныетелеметрии, виртуальные миры) допускают применение ИКМ.
24.
Вейвлетное сжатие — общее название класса методов кодирования изображений, использующих двумерное вейвлет -разложение кодируемого изображения или его частей. Обычно подразумевается сжатие с потерей качества.
Существенную роль в алгоритмах вейвлетной компрессии играет концепция представления результатов вейвлет-разложения в виде нуль-дерева (zero-tree).
Упорядоченные в нуль-дереве битовые плоскости коэффициентов вейвлет-разложения огрубляются и кодируются далее с использованием статистических методов сжатия.
25.
Свойства вейвлета,
· Локализация. Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его "средняя" частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его "среднюю" частоту и ширину спектра также вдвое.
Вейвлетную функцию можно считать хорошо локализованной при выполнении условий:
|
|
(t) ≤ C/(1+|t|)1+, (f) ≤ C/(1+|f|)1+, С=const, при > 0.
· Нулевое среднее значение, т.е. выполнение условия для нулевого момента:
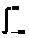 (t) dt = 0,
(t) dt = 0,
что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов, нулевое значение частотного спектра вейвлета при =0, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте 0. Для анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:
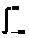 tm(t) dt = 0.
tm(t) dt = 0.
Такие вейвлеты называются вейвлетами m-го порядка.
· Ограниченность. Необходимое и достаточное условие:
||(t)||2 = 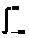 |(t)|2 dt < ¥
|(t)|2 dt < ¥
Оценка ограниченности и локализации может выполняться с использованием выражений:
|(t)| < 1/(1+|t|n), или |(ω)| < 1/(1+|ωo|n),
где o – средняя частота вейвлета. Число n должно быть как можно больше.
· Автомодельность базиса или самоподобие. Форма всех базисных вейвлетов ab(t) должна быть подобна материнскому вейвлету (t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.
26.
Дискретное
Вейвлеты, образующие ДВП, могут рассматриваться как разновидность фильтра конечного импульсного отклика.
Применение: обычно используется для кодирования сигналов (инженерное дело, компьютерные науки)