В компьютерной томографии линейка детекторов измеряет поглощение исследуемым объектом параллельного пучка излучения (например, рентгеновских лучей в медицинской томографии, сейсмических волн в геофизической томографии). В соответствии сзаконом Бугера-Ламберта-Бера
интенсивность излучения, измеряемая детектором в точке s линейки пропорциональна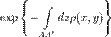
, где 
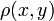оптическая плотность объекта для данного типа излучения, а интеграл берётся вдоль прямой 
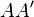проходящей через данный детектор и перпендикулярной линейке детекторов (z — координата на этой прямой). Соответственно, логарифм от интенсивности, взятый с обратным знаком, даёт преобразование Радона от оптической плотности. Вращая всю систему из источника излучения и детекторов вокруг объекта (при этом оставаясь в одной плоскости), или вращая сам объект вокруг оси, перпендикулярной плоскости, показаной на рисунке, получают достаточно полную информацию о преобразовании Радона оптической плотности в данном срезе объекта. Используя обратное преобразование Радона можно восстановить поглощение излучения в любой точке данной плоскости объекта.
10.
Преобразование Гильберта
В математике и обработке сигналов преобразование Гильберта — линейный оператор, сопоставляющий каждой функции u(t) функцию H(u)(t) в той же области.
Преобразование Гильберта может быть определено в смысле главного значения интеграла по Коши:
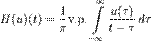
Или, более явно:
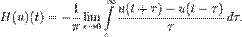
При двукратном применении преобразования Гильберта функция меняет знак:
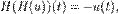
при условии, что оба преобразования существуют.
Связь с преобразованием Фурье
Преобразование Гильберта является множителем в спектральной области.
|
|
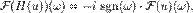
где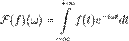 
— вариант прямого преобразования Фурье без нормировочного множителя.
[править]Обратное преобразование
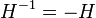
11.
Преобразование Адамара
Самым простым унитарным преобразованием является преобразование Адамара. Матрица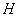 
для случая двух случайных величин будет иметь вид:
.
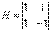Если из элементов матрицы 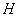составить базисные вектора 
, 
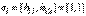, то они будут характеризовать поворот ортогональной системы координат на 45° относительно единичного базиса.
Если случайные величины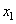 
и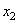 
имеют корреляционную зависимость 
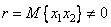, то проекция вектора 
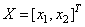на базисный вектор 
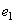будет, в среднем, больше, чем проекция этого же вектора на базисный вектор 
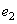. Благодаря этому информация будет сосредотачиваться в первом коэффициенте преобразования. Второй коэффициент служит для уточнения представления вектора 
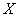в новом базисе.
Рассмотрим подробнее процесс разложения вектора 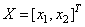по базисным векторам Адамара. Проекция 
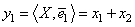представляет собой удвоенное среднее значение элементов вектора 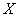, проекция 
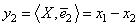- удвоенную разность между средним значением и элементом 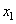(рис. 2).
Рис. 2. Графическое представление проекций
Выполним восстановление вектора 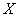по первому коэффициенту 
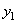с помощью обратной матрицы 
, получим:
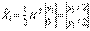. (5)
Из выражения (5) видно, что восстановленный вектор 
представляет собой средние значения элементов 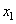и 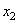, что соответствует «грубому» приближению вектора 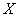, без наличия мелких деталей.
Рассмотрим теперь восстановление того же вектора по коэффициенту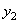 
, получим:
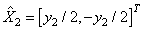. (6)
Анализ выражения (6) показывает, что вектор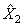 
описывает только мелкие детали вектора 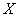. При этом можно заметить, что сумма 
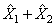даст исходный вектор 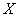, что соответствует восстановлению по обоим коэффициентам разложения.
|
|
При увеличении размерности пространства большая часть информации будет сосредоточена в малом числе коэффициентов
Матрицу Адамара размерности 4х4 элементов легко построить из матрицы Адамара 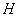размерностью 2х2 элемента:
,
Пользуясь данным соотношением можно построить матрицу Адамара любой размерности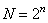 
, где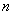 
- любое целое положительное число.
Анализ изображений выполняется на основе разделимого преобразования:
.
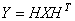Так как матрица 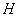представляет собой оператор ортогонального преобразования, то обратное преобразование из 
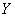в 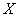запишется в виде
.
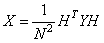Восстановление изображения 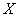по неполному числу коэффициентов разложения, также как и для случая двух случайных величин, будет приводить к похожим эффектам сглаживания и выделения мелких деталей. При этом возникают ошибки восстановления 
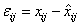, которым можно поставить в соответствие некоторую функцию потерь 
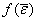. Значение этой функции будет характеризовать качество восстановления. На практике часто используют квадратичную функцию потерь
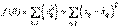. (7)
Так как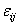 
носит случайный характер, то значение 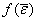также является случайной величиной. При этом желательно, чтобы 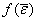, в среднем, была минимальна. Для этого перепишем выражение (7) в виде
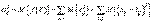, (8)
где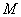 
- знак математического ожидания. Найдем базисные вектора, минимизирующие (8).
15.