Дискретное вейвлет-преобразование (DWT) - реализация вейвлет-преобразования с использованием дискретного набора масштабов и переносов вейвлета, подчиняющихся некоторым определённым правилам. Другими словами, это преобразование раскладывает сигнал на взаимно ортогональный набор вейвлетов, что является основным отличием от непрерывного вейвлет-преобразования (CWT), или его реализации для дискретных временных рядов, иногда называемой непрерывным вейвлет-преобразованием дискретного времени (DT-CWT).
Вейвлет может быть сконструирован из функции масштаба, которая описывает свойства его масштабируемости. Ограничение, что функция масштаба должна быть ортогональна к своим дискретным преобразованиям, подразумевает некоторые математические ограничения на них, которые везде упоминаются, т.е. уравнение гомотетии
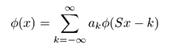
где S - фактор масштаба (обычно выбирается как 2). Более того, площадь под функцией должна быть нормализована и функция масштабирования должна быть ортогональна к своим численным переносам, т.е.
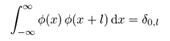
После введения некоторых дополнительных условий (поскольку вышеупомянутые ограничения не приводят к единственному решению) мы можем получить результат всех этих уравнений, т.е. конечный набор коэффициентов ak которые определяют функцию масштабирования, а также вейвлет. Вейвлет получается из масштабирующей функции как N где N - чётное целое. набор вейвлетов затем формирует ортонормированный базис, который мы используем для разложения сигнала. Следует отметить, что обычно только несколько коэффициентов ak будут ненулевыми, что упрощает расчёты.
На следующем рисунке показаны некоторые масштабирующие функции и вейвлеты. Наиболее известным семейством ортонормированных вейвлетов явлется семейство Добеши. Её вейвлеты обычно обозначаются числом ненулевых коэффициентов ak, таким образом, мы обычно говорим о вейвлетах Добеши 4, Добеши 6, и т.п. Грубо говоря, с увеличением числа коэффициентов вейвлета функции становятся более гладкими. См. сравнение вейвлетов Добеши 4 и 20 ниже. Другой из упомянутых вейвлетов - простейший вейвлет Хаара, который использует прямоугольный импульс как масштабирующую функцию.
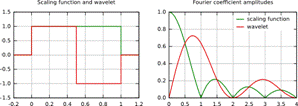
Функция масштабирования Хаара и вейвлет (слева) и их частотные составляющие (справа).
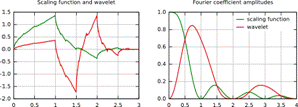
Функция масштабирования Добеши 4 и вейвлет (слева) и их частотные составляющие (справа).
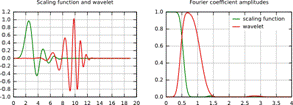
Функция масштабирования Добеши 20 и вейвлет (слева) и их частотные составляющие (справа).
Существует несколько видов реализации алгоритма дискретного вейвлет-преобразования. Самый старый и наиболее известный – алгоритм Малла (пирамидальный). В этом алгоритме два фильтра – сглаживающий и несглаживающий составляются из коэффициентов вейвлета и эти фильтры рекуррентно применяются для получения данных для всех доступных масштабов. Если используется полный набор данных D = 2N и длина сигнала равна L, сначала рассчитываются данные D/2 для масштаба L/2N - 1, затем данные (D/2)/2 для масштаба L/2N - 2, … пока в конце не получится 2 элемента данных для масштаба L/2. результатом работы этого алгоритма будет массив той же длины, что и входной, где данные обычно сортируются от наиболее крупных масштабов к наиболее мелким.
В Gwyddion для расчёта дискретного вейвлет-преобразования используется пирамидальный алгоритм. Дискретное вейвлет-преобразование в двумерном пространстве доступно в модуле DWT.
Дискретное вейвлет-преобразование может использоваться для простого и быстрого удаления шума с зашумлённого сигнала. Если мы возьмём только ограниченное число наиболее высоких коэффициентов спектра дискретного вейвлет-преобразования, и проведём обратное вейвлет-преобразование (с тем же базисом) мы можем получить сигнал более или менее очищенный от шума. Есть несколько способов как выбрать коэффициенты, которые нужно сохранить. В Gwyddion реализованы универсальный порог, адаптивный по масштабу порог [ 2 ] и адаптивный по масштабу и пространству порог [ 3 ]. Для определения порога в этих методах мы сперва определяем оценку дисперсии шума, заданную
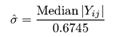
где Yij соответствует всем коэффициентам наиболее высокого поддиапазона масштаба разложения (где, как предполагается, должна присутствовать большая часть шума). Или же дисперсия шума может быть получена независимым путём, например, как дисперсия сигнала АСМ когда сканирование не идёт. Для наиболее высокого поддиапазона частот (универсальный порог) или для каждого поддиапазона (для адаптивного по масштабу порога) или для окружения каждого пикселя в поддиапазоне (для адаптивного по масштабу и пространству порога) дисперсия рассчитывается как
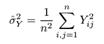
Значение порога считается в конечном виде как
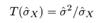
где
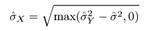
Когда порог для заданного масштаба известен, мы можем удалить все коэффициенты меньше значения порога (жесткий порог) или мы можем уменьшит абсолютное значение этих коэффициентов на значение порога (мягкий порог).
30.
Вейвле́ты (от англ. wavelet), всплески (гораздо реже [1] — вэйвле́ты) — это математическиефункции, позволяющие анализировать различные частотные компоненты данных. Однако это частное определение — в общем случае анализ сигналов производится в плоскости вейвлет-коэффициентов (масштаб — время — уровень) (Scale-Time-Amplitude). Вейвлет-коэффициенты определяются интегральным преобразованием сигнала. Полученные вейвлет-спектрограммы принципиально отличаются от обычных спектров Фурье тем, что дают четкую привязку спектра различных особенностей сигналов ко времени.
Существует несколько подходов к определению вейвлета: через масштабный фильтр, масштабную функцию, и вейвлет-функцию. Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Вейвлетные функции могут быть симметричными, асимметричными и несимметричными, с компактной областью определения и не имеющие таковой, а также иметь различную степень гладкости.
]Примеры вейвлетов
§ вейвлет Хаара
§ вейвлеты Добеши
§ вейвлеты Гаусса
§ вейвлет Мейера
§ вейвлеты Морле
§ вейвлет Пауля
§ вейвлет MHat («Мексиканская шляпа»)
§ вейвлеты Р. Койфмана — койфлеты
§ вейвлет Шеннона
Вейвлет Хаара
Вейвлет Хаа́ра — один из первых и наиболее простых вейвлетов. Он был предложен венгерским математиком Альфредом Хааром в 1909 году. Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими. Впоследствии Ингрид Добеши стала развивать теорию ортогональных вейвлетов и предложила использовать функции, вычисляемые итерационным путем, названные вейвлетами Добеши.
Построение вейвлета Хаара
Родительская (материнская) вейвлет-функция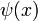 
с нулевым значением интеграла 
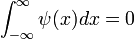, определяющая детали сигнала, задается следующим образом:
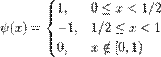
Масштабирующая функция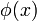 
с единичным значением интеграла 
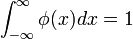, определяющая грубое приближение (аппроксимацию) сигнала, постоянна: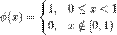 
Преобразование Хаара
Вейвлет Добеши порядка 2
Вейвлеты Добеши (англ. Daubechies Wavelet) — семейство ортогональных вейвлетов с компактным носителем, вычисляемым итерационным путем. Названы в честь математика из США, первой построившей данное семейство, Ингрид Добеши.
Построение вейвлетов Добеши
Для построения вейвлетов воспользуемся уравнением растяжения и вейвлет-уравнением
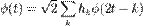
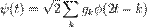
Компактность носителя функций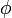 
и 
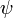может быть достигнута, если будет выбрано конечное число 
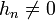таким образом, чтобы была достигнута ортогональность и гладкость вейвлета, либо чтобы выполнялось условие моментов. Для области Фурье условие ортогональности и гладкости выглядит следующим образом:
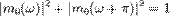, где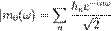 
— тригонометрический полином,
при условии моментов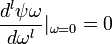 
,для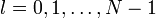 
принимающий вид:
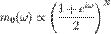
Если положить, что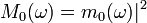 
— полином по 
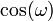, то условие нулевых моментов дает 
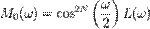, где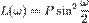 
— полином по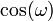
Для поиска коэффициентов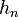 
необходимо получить 
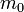, выделив форму полинома 
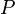. Из условия ортогональности и условия нулевых моментов следует, что
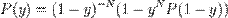(1)
Разложив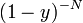 
до порядка 
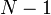, получим явный вид полинома:
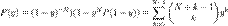
Путем спектрального разложения на множители можно извлечь корни 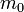из :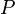
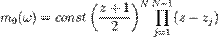
Искомые коэффициенты вейвлета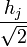 
будут являться коэффициентами при 
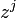в обратном порядке.
Также для построения вейвлетов данного типа используется каскадный алгоритм. Он позволяет поточечно строить масштабирующую функцию φ по известным коэффициентам 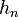. На каждом шаге алгоритма функция φ уточняется по оси t в 2 раза. Далее при необходимости применяется сглаживание φ. После этого, зная φ и 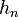, находится функция самого вейвлета ψ.
38.
Пространственная фильтрация
Чтобы понять влияния различных форм пространственной фильтрации, нам необходимо взглянуть на двухмерные спектры как временных, так и пространственных частот внутри сейсмограммы. Существует четкое соответствие между временными / частотными областями и пространственными / волновыми областями. Рассмотрим простой «треугольный» фильтр, при значениях дискретизации 1, 2, 3, 2, 1. Во временной области он (и его амплитудные спектры) выглядят следующим образом:
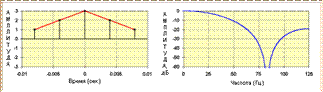Временные дискреты (через каждые 4 мсек) преобразуются в функцию «типа синхронизации» в частотной области. Теперь рассмотрим ту же функцию в пространстве: 
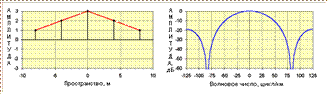Кроме осей и того, что в пространстве мы рассматриваем и положительные, и отрицательные волновые числа, эти два рисунка идентичны.
|
40.
Белый шум содержит частоты одинаковой вероятности =>преобразование Фурье даст постоянное значение.
Шум описываеться функцией плотности распределения вероятности
Основное значение шума:среднее значение,средне-квадратичная степененная дисперсия.
Гаусов шум-шум в электрических цепях и датчиках-иъх вносит в наш сигнал описывают спомощью Гаусова шума.
Шум Релея-возникает на снимках,снятых с блиского расстояния.
41.
Медиа́нный фи́льтр — один из видов цифровых фильтров, широко используемый в цифровой обработке сигналов и изображений для уменьшения уровня шума. Медианный фильтр является нелинейнымКИХ-фильтром.
Значения отсчётов внутри окна фильтра сортируются в порядке возрастания (убывания); и значение, находящееся в середине упорядоченного списка, поступает на выход фильтра. В случае четного числа отсчетов в окне выходное значение фильтра равно среднему значению двух отсчетов в середине упорядоченного списка. Окно перемещается вдоль фильтруемого сигнала и вычисления повторяются.
Медианная фильтрация — эффективная процедура обработки сигналов, подверженных воздействию импульсных помех.
42.
Рассмотрим операции, осуществляемые в пространственной области над отсчетами цифрового изображения (пикселями) с целью повышения качества этого изображения. А именно класс операций, относящийся к методу нелинейной медианной фильтрации.
Этот метод наиболее эффективен, если шум на изображении имеет импульсный характер и представляет собой ограниченный набор пиковых значений на фоне нулей. Медианный фильтр реализуется как процедура локальной обработки скользящим окном различной формы (маской), которое включает нечетное число отсчетов изображения, и заключается в том, что для каждого положения окна попавшие в него отсчеты упорядочиваются по возрастанию (убыванию) значений. Средний отчет в этом списке называется медианой рассматриваемой группы из N отсчетов. Эта медиана заменяет центральный отсчет в окне для обработанного сигнала. В результате применения медианного фильтра наклонные участки и резкие перепады значений яркости на изображениях не изменяются. Это очень полезное свойство именно для изображений, на которых, как известно, контуры несут основную информацию. В то же время импульсные помехи, протяженность которых составляет менее половины окна, будут подавлены.
Медианная фильтрация имеет и свои недостатки. В частности, экспериментально установлено, что у данного метода относительно слабая эффективность при фильтрации так называемого флуктуационного шума. Кроме того, при увеличении размера маски происходит размытие контуров изображения и, как следствие, снижение четкости изображения.
Указанные недостатки метода можно уменьшить до минимума, если воспользоваться медианной фильтрацией с динамическим размером маски (адаптивной медианной фильтрацией).
Принцип вычисления центрального отсчета при локальной обработке изображения скользящим окном остается все тот же. Эта медиана из набора упорядоченных отсчетов, попавших в окно (маску), а размер скользящего окна (маски) динамический и зависит от яркости соседних пикселей.
Введем пороговый коэффициент отклонения яркости Sthreshold = [0, 1]. Величины отклонения яркости соседних пикселей A (r, n, m), попавших в окно размером n x m, относительно яркости центрального отсчета A (r) запишутся в виде (1)
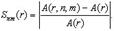
Тогда критерий, согласно которому необходимо увеличивать размер маски с центральным отсчетом r, будет иметь вид (2)
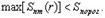
На основе описанного алгоритма была разработана компьютерная программа, подтвердившая на практике преимущества адаптивной медианной фильтрации.