Окно Блэкмана
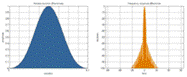
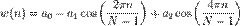
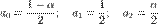
Уровень боковых лепестков: -58 дБ (α=0.16).
5.
Окно Кайзера
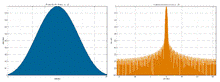
Окно Кайзера, α =2; B=1.5
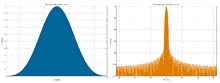
Окно Кайзера, α =3; B=1.8
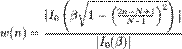
где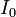 
— модифицированная функция Бесселя первого рода нулевого порядка; 
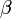— коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше 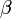тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.
6.
Свёртка фу́нкций — операция в функциональном анализе, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на группах, а также мер. В математике, свёртка — это математическая операция двух функций f и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования.
9.
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математикаИоганна Радона
1917-го года[1].Важнейшее свойство преобразования Радона — обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.
Двумерное преобразование Радона
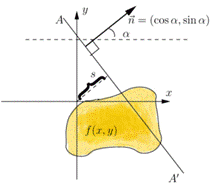
Двумерное преобразование Радона.
В данном случае R(s,α) есть интеграл от f(x,y) вдоль прямой AA'
Рассмотрение преобразования Радона удобно начать с простейшего случая функции двух переменных, к тому же, именно этот случай наиболее практически важен.
Пусть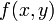 
функция двух действительных переменных, определённая на всей плоскости и достаточно быстро убывающая на бесконечности (так, чтобы соответствующие несобственные интегралы сходились). Тогда преобразованием Радона функции 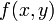называется функция
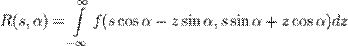(1)
Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной вектору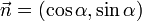 
и проходящей на расстоянии s (измеренного вдоль вектора 
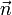, с соответствующим знаком) от начала координат.
Связь преобразования Радона и преобразования Фурье. Формула обращения
Рассмотрим двумерное преобразование Фурье от функции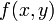
. (*)
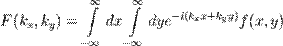Можно заметить, что показатель экспоненты в этом интеграле не изменяется, если мы двигаемся вдоль прямой перпендикулярной вектору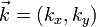 
, и изменяется наиболее быстро если мы движемся вдоль этого вектора. Поэтому удобно перейти к новым переменным. Обозначим 
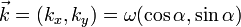, мы выберем новые переменные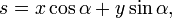 
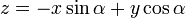. Сделав замену переменных в интеграле, получаем
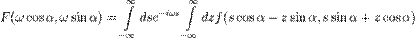
т.е.
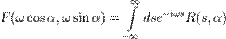
Таким образом, одномерное преобразование Фурье по переменной s от преобразования Радона функции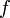 
даёт нам двумерное преобразование Фурье от функции 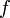. Поскольку двумерное преобразование Фурье достаточно хорошей функции обратимо, то обратимо и преобразование Радона.
Формула обращения для двумерного преобразования Фурье, как известно, выглядит следующим образом
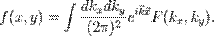
Для наших целей удобно переписать эту формулу в полярных координатах
,
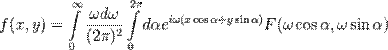что немедленно даёт формулу обращения преобразования Радона
,
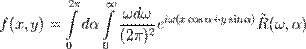где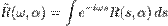 
.