СЛЕДСТВИЯ ИЗ АКСИОМ АБСОЛЮТНОЙ ГЕОМЕТРИИ

Во всех утверждениях словосочетание «две прямые» («две точки», «две плоскости») означает: две различные прямые (точки, плоскости).

Следствия из аксиом I группы:

1. Доказать, что две прямые не могут иметь более одной общей точки.

2. Доказать, что если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (1₇, 1₁, 1₆)

3. Доказать, что плоскость и не принадлежащая ей прямая могут иметь не более одной общей точки.

4. Доказать, что через прямую а и не принадлежащую ей точку С проходит единственная плоскость

5. Доказать, что через две пересекающиеся прямые проходит единственная плоскость.

6. Существует хотя бы одна точка, не принадлежащая данной прямой.(I₃)

7. Существует хотя бы одна точка, не принадлежащая данной плоскости (I₈)

8. Для любых точек А и В существует по крайней мере одна точка С такая, что А, В, С не лежат на одной прямой.

9. Для любых точек А и В существуют по крайней мере две точки С и D такие, что А, В, С, D не лежат в одной плоскости.

10. Доказать, что для любой точки А существуют по крайней мере две точки В и С такие, что А, В, С не лежат на одной прямой.

Указание. По 1₃ (пусть существуют точки К, М, Р; Если точка А совпала с одной из них, то …; если А не совпала ни с одной из них, то … - перебор случаев).

11. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.

Следствия из аксиом II группы:

ВАЖНЫЕ ПОНЯТИЯ:

 

Отрезок [ ХY ] пересекает прямую m, если прямая (XY) пересекает прямую m в такой точке Z, что X – Z – Y (т.е. Z лежит между Х и Y).

Точки Х и Y лежат по разные стороны от прямой m (X, Y ¸ m), если отрезок [ XY ] пересекает прямую m во внутренней точке.

Точки Х и Y лежат по одну сторону от прямой m, если: 1) эти точки и прямая лежат в одной плоскости; 2) отрезок [ XY ] и прямая m не имеют общих точек.

Треугольник – фигура, состоящая из трех точек (называемых вершинами треугольника), не принадлежащих одной прямой, и трех отрезков (называемых сторонами треугольника) с концами в этих точках.

 

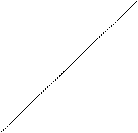
12. Доказать, что для любых двух точек А и В существует хотя бы одна точка Р, лежащая между ними.

Указание. Необходимо сконструировать такую точку, опираясь на аксиомы 1-2-й групп: I₃(А, В, С), II₂(В, С, М), II₂(М, А, N), II₄(, прямая СN).

М

С

 

 

А Р В

 

N

 

 

13. Из трех точек прямой одна и только одна лежит между двумя другими.

14. Доказать, что если прямая а не проходит через вершины треугольника АВС, то она не может пересекать всех трех сторон треугольника.

Указание. От противного; пусть Е-F-G. Рассмотреть треугольник ВЕG и прямую АС:

Е F

 

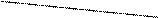В G

С

а

 

ВАЖНО!

1) Точки Х и Y лежат по разные стороны от прямой m, если отрезок XY пересекает прямую m во внутренней точке Z (т.е. Z лежит между Х и Y). Говорят, что точки Х и Y лежат по одну сторону от прямой m, если: 1) эти точки и прямая лежат в одной плоскости;

2) отрезок ХY и прямая m не имеют общих точек.

 

15. 1) Теорема о полуплоскости. Каждая прямая а, лежащая в плоскости , разбивает множество всех точек этой плоскости, не принадлежащих прямой а, на два непустых подмножества так, что любые две точки одного подмножества лежат по одну сторону от прямой а, а любые две точки из разных подмножеств лежат по разные стороны от прямой а.

Определение. Каждое подмножество точек плоскости, определённое в теореме, называется полуплоскостью.

Доказательство Обозначим множество всех точек плоскости, не принадлежащих прямой а. Введём в этом множестве некоторое бинарное отношение . Будем считать, что точки А и В множества находятся в отношении («дельта»), если они либо совпадают, либо лежат по одну сторону от прямой а. Это отношение является отношением эквивалентности (рефлексивно, симметрично и транзитивно – показать самостоятельно; транзитивность - от противного). Тогда разбивается на классы эквивалентности по отношению 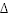. Докажем, что таких класса всего два.

Возьмём точку М плоскости, не принадлежащую прямой а (объясните, почему такая точка существует). Возьмём точку Р, принадлежащую прямой а (объясните, почему такая точка существует).Возьмём такую точку N, что М-Р-N (объясните, почему такая точка существует). Тогда М 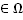, N 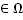, причем М и N лежат по разные стороны от прямой а (М,N а). Возьмём класс точки М и класс точки N. Покажите самостоятельно, что эти классы не пересекаются (не имеют ни одной общей точки – от противного). Покажите, что любая точка множества принадлежит либо классу К_М, либо классу К_N (применив теорему Паша).

 

2) Теорема о луче. Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.

Указание. Существует точка А, не принадлежащая прямой l. Существует плоскость, проходящая через точку А и прямую l. Существует прямая ОА. Эта прямая делит множество всех точек плоскости, не принадлежащих ей, на две полуплоскости ₁ и ₂. Рассмотрим два множества: К₁ –пересечение ₁ и l, К₂ –пересечение ₂ и l. Докажите, что эти множества удовлетворяют требованию теоремы.

 

Определение. Каждое подмножество точек прямой, определённое в теореме, называется лучом. Точка О – начало лучей. Два луча с общим началом, принадлежащие одной прямой, называются дополнительными друг к другу лучами.

 

16. Если А-С-В и А-D-С, то А-D-В.

Краткое решение. Рассмотрим лучи СА и СВ. Так как А-D-С, то точка D принадлежит лучу СА, следовательно, D-С-В. Рассмотрим лучи DA и DB. Так как D-С-В, то точка С принадлежит лучу DB, следовательно, А-D-В.

 

17. На каждом отрезке, луче и прямой существуют бесчисленное множество точек. (Указать алгоритм поиска точек)

Определение. Угол – фигура, состоящая из двух лучей с началом в одной точке (иногда угол определяют так: фигура, состоящая из точки, и двух лучей с началом в этой точке). Эти два луча называются сторонами угла, а их начало – вершиной угла.

Если стороны угла – дополнительные лучи, то угол называется развёрнутым.

Если два угла имеют общую сторону, а две другие их стороны являются дополнительными лучами, то углы называются смежными.

Если стороны одного угла являются дополнительными лучами сторон другого угла, то эти углы называются вертикальными.

Угол называется прямым (обозначается d, от французского droit – прямой), если он конгруэнтен смежному с ним углу. Можно доказать, что любые два прямых угла конгруэнтны.

2) Точка М называется внутренней точкой неразвернутого угла АВС, если она лежит в полуплоскостью с границей (ОА), содержащей точку В и в полуплоскостью с границей (ОВ), содержащей точку А. Множество всех внутренних точек угла называется внутренней областью угла.

Луч l называется внутренним лучом угла, если его начало совпадает с вершиной этого угла и все его точки являются внутренними точками угла.

 

Или Внутренняя область угла АОВ – это пересечение двух полуплоскостей ₁ и ₂, где ₁ – полуплоскость с границей ОА, содержащая точку В, ₂ – полуплоскость с границей ОВ, содержащая точку А.

 

18. Доказать, что если М – внутренняя точка угла АОВ, то луч ОМ – внутренний луч угла АОВ. Указание. Надо доказать, что каждая точка К луча ОМ – внутренняя точка угла АОВ, то есть К ₁ и К ₂. Для точки М: М и А лежат по одну сторону от ОВ, М и В лежат по одну сторону от ОА. К – точка луча ОМ, значит, К и М лежат по одну сторону от прямой ОА, К и М лежат по одну сторону от прямой ОВ, и т.д.

19. Если точки М и N лежат на различных сторонах угла АОВ, то любая точка, лежащая между М и N, есть внутренняя точка угла АОВ.

20. Любой внутренний луч угла пересекает любой отрезок с концами на разных сторонах угла.

 

 

мэC4-1 1 Сформулировать аксиомы I-2, I-6, I-8, II-1, II-4, III-1, III-4 2. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.	мэC4-2 1 Сформулировать аксиомы I-1, I-3, I-7, II-2, II-3, III-2, III-5 2. Доказать:Если А-С-В и А-D-С, то А-D-В.
мэC4-3 1 Сформулировать аксиомы I-2, I-3, I-6, II-2, II-4, III-3, III-4 2. Доказать, что через две пересекающиеся прямые проходит единственная плоскость	мэC4-3 1 Сформулировать аксиомы I-1, I-5, I-8, II-2, II-3, III-3, III-4 2. Теорема о луче.Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.
мэC4-1 1 Сформулировать аксиомы I-2, I-6, I-8, II-1, II-4, III-1, III-4 2. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.	мэC4-2 1 Сформулировать аксиомы I-1, I-3, I-7, II-2, II-3, III-2, III-5 2. Доказать:Если А-С-В и А-D-С, то А-D-В.
мэC4-3 1 Сформулировать аксиомы I-2, I-3, I-6, II-2, II-4, III-3, III-4 2. Доказать, что через две пересекающиеся прямые проходит единственная плоскость	мэC4-3 1 Сформулировать аксиомы I-1, I-5, I-8, II-2, II-3, III-3, III-4 2. Теорема о луче.Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.
мэC4-1 1 Сформулировать аксиомы I-2, I-6, I-8, II-1, II-4, III-1, III-4 2. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.	мэC4-2 1 Сформулировать аксиомы I-1, I-3, I-7, II-2, II-3, III-2, III-5 2. Доказать:Если А-С-В и А-D-С, то А-D-В.
мэC4-3 1 Сформулировать аксиомы I-2, I-3, I-6, II-2, II-4, III-3, III-4 2. Доказать, что через две пересекающиеся прямые проходит единственная плоскость	мэC4-3 1 Сформулировать аксиомы I-1, I-5, I-8, II-2, II-3, III-3, III-4 2. Теорема о луче.Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.
мэC4-1 1 Сформулировать аксиомы I-2, I-6, I-8, II-1, II-4, III-1, III-4 2. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.	мэC4-2 1 Сформулировать аксиомы I-1, I-3, I-7, II-2, II-3, III-2, III-5 2. Доказать:Если А-С-В и А-D-С, то А-D-В.
мэC4-3 1 Сформулировать аксиомы I-2, I-3, I-6, II-2, II-4, III-3, III-4 2. Доказать, что через две пересекающиеся прямые проходит единственная плоскость	мэC4-3 1 Сформулировать аксиомы I-1, I-5, I-8, II-2, II-3, III-3, III-4 2. Теорема о луче.Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.

 

21..

22. На любой плоскости существуют хотя бы три точки, не лежащие на одной прямой.

 

2) Теорема о луче. Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.

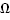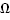Указание. Существует точка А, не принадлежащая прямой l. Существует плоскость, проходящая через точку А и прямую l. Существует прямая ОА. Эта прямая делит множество всех точек плоскости, не принадлежащих ей, на две полуплоскости ₁ и ₂. Рассмотрим два множества: К₁ –пересечение ₁ и l, К₂ –пересечение 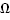₂ и l. Докажите, что эти множества удовлетворяют требованию теоремы.

 

Определение. Каждое подмножество точек прямой, определённое в теореме, называется лучом. Точка О – начало лучей. Два луча с общим началом, принадлежащие одной прямой, называются дополнительными друг к другу лучами.

 

23. Если А-С-В и А-D-С, то А-D-В.

Краткое решение. Рассмотрим лучи СА и СВ. Так как А-D-С, то точка D принадлежит лучу СА, следовательно, D-С-В. Рассмотрим лучи DA и DB. Так как D-С-В, то точка С принадлежит лучу DB, следовательно, А-D-В.

 

24. На каждом отрезке, луче и прямой существуют бесчисленное множество точек. (Указать алгоритм поиска точек)

25. Доказать, что если М – внутренняя точка угла АОВ, то луч ОМ – внутренний луч угла АОВ.