Цель работы: вычислить ускорение свободного падения из формулы для периода колебаний математического маятника.
Оборудование: часы с секундной стрелкой, измерительная лента, шарик с отверстием, нить, штатив с муфтой и кольцом.
Теория:
Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью такого маятника может служить шарик, подвешенный на длинной нити.
Период колебаний на зависит от массы маятника и амплитуды его колебаний, если угол размаха не превышает 60.
Период колебаний математического маятника прямо пропорционален корню квадратному из длины нити и обратно пропорционален корню квадратному из ускорения свободного падения
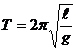
Из этой формулы можно выразить ускорение свободного падения
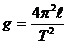
Порядок выполнения работы:
1. Установите на краю стола штатив. У его верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3 – 5 см от пола.
2. Отклоните маятник от положения равновесия на 5 – 8 см и отпустите его.
3. Измерьте длину подвеса мерной лентой.
4. Измерьте время Δt 40 полных колебаний (N).
5. Повторите измерения Δt (не изменяя условия опыта) и найдите среднее значение Δtср.
6. Вычислите среднее значение периода колебаний Тср по среднему значению Δtср.
7. Вычислите значение по формуле: 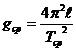
8. Полученные результаты занесите в таблицу.
1. Сравните полученное среднее значение со значением g=9,8 м/с2
и рассчитайте относительную погрешность измерения по формуле
δ = 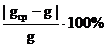
Результаты измерений:
| № опыта | Длина подвеса ℓ, м | Число колебаний N | Время колебаний Δt, с | Среднее значение времени колебаний Δtср, с | Среднее значение периода колебаний Тср, с | Среднее значение ускорения свобод- ного падения gср, м/с2 | Табличное значение ускорения свобод- ного падения g, м/с2 | Относительная погрешность δ, % |
Расчеты:
Δtср =
Тср = 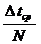
Тср =
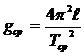
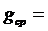
δ = 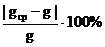
δ =
Вывод:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответы на вопросы:
1. Какими должны быть нить и подвешенный к ней груз, чтобы маятник можно было считать математическим?
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Как изменится период колебаний пружинного маятника, если заменить груз другим, по массе вдвое меньшим?
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3. Как изменится период колебаний математического маятника, если уменьшить длину нити в 4 раза?
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Дополнительные задания
Вариант 1.
1. На пружине жесткостью 100 Н/м подвешено тело. Если вывести пружину из положения равновесия, то оно колеблется, делая 300 колебаний в минуту. Найти массу тела.
2. Написать уравнение гармонического колебания, если амплитуда равна 5см, а период колебаний 1 с.
Вариант 2.
1. Тело массой 200 г совершает колебания на пружине жесткостью 16 Н/м. Определить период и частоту колебаний.
2. Дано уравнение, описывающее гармоническое колебание x =10 Sin 2πt. Определить амплитуду, период и частоту колебаний.
Решение задач:
Домашнее задание:
1. Написать уравнение гармонического колебания, если амплитуда равна 0,2 м, период колебаний 0,1 с, а начальная фаза равна нулю.
2. За 20 с маятник совершил 10 колебаний, длина маятника 1м. Определить ускорение свободного падения маятника.
Лабораторная работа №14