| n | ||||||||||
lgn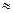 
| 0,30 | 0,48 | 0,60 | 0,70 | 0,78 | 0,85 | 0,90 | 0,95 |
Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 
(плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i- го частичного прямоугольника равна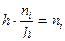 
- сумме частот вариант i- го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению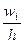 
(плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 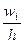. Площадь i- го частичного прямоугольника равна - 
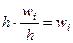относительной частоте вариант, попавших в i- й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.
Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.
Генеральная средняя
Определение. Генеральной средней 
называют среднее арифметическое значение признака генеральной совокупности:
|
|
,
где N - объем совокупности.
Выборочная средняя
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема п.
Выборочной средней 
называют среднее арифметическое значение признака выборочной совокупности:
, или 
.
хi – варианта выборки, пi – частота варианты хi, 
- объем выборки.
Рассмотрим некоторую совокупность, значений количественного признака Х объема п:
| Значение признака | х1 | х2 | … | хк |
| Частота | п1 | n2 | … | пк |
причем 
.
Отклонением называют разность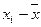 
между значением признака и общей средней.
Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю
.
Генеральная дисперсия
Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику – генеральную дисперсию.
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:
.
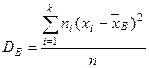Более удобна формула: 
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
.
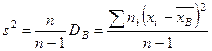Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выброчной дисперсии:
|
|
.
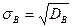Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:
.
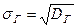Стандартное отклонение. Стандартное (среднеквадратичное) отклонение (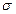
) – это положительный квадратный корень из дисперсии. Оно вычисляется в тех же единицах (размерностях), что и исходные данные и характеризует степень рассеивания вариационного ряда вокруг средней. Чем меньше 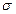, тем более типична, точна средняя.