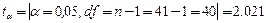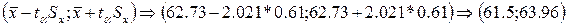Нормальное распределение впервые было найдено Абрахамом де Муавром в первой половине XVIII в. (1733г). Затем в начале XIX в. было использовано в работах Гаусса и Лапласа и, по существу, было открыто заново. Под влиянием классических работ Гаусса и Лапласа долгие годы считалось непререкаемой истиной, что все возможные распределения при достаточно большом количестве наблюдений приближаются к нормальному распределению, как некоему идеалу. Подобное утверждение, безусловно, слишком смелое, но тем не менее множество биологических и медицинских показателей, таких как показатели физического развития (вес, рост, давление, температура тела, уровень гормонов), составляющие плазмы крови, демографические и другие показатели следуют нормальному распределению.
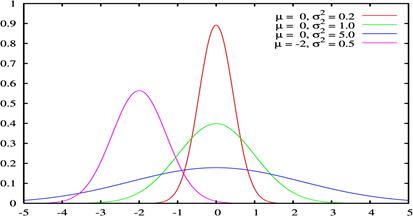
Нормальное распределение представляет собой семейство кривых. Каждая кривая это колоколообразный график, на котором по горизонтальной оси откладывается величина эффекта, а на вертикальной – количество пациентов, у которых наблюдался эффект данной величины.
Кривая полностью определяется двумя параметрами, средним и среднеквадратическим отклонением. Факт указанного распределения записывают таким образом: 
.
Основные характеристики нормального распределения:
- равенство числовых характеристик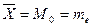 
(среднее, мода и медиана равны между
собой);
- симметричность отклонений от среднего значения;
- общая площадь под кривой равна 1;
- хвосты кривой в обоих направлениях уходят в бесконечность, непрерывно приближаясь, но,
никогда не касаясь, горизонтальной оси, т.е. хвосты асимптотически стремятся к
горизонтальной оси;
- форма кривой определяется среднеквадратическим отклонением генеральной совокупности;
|
|
- распределениям с малыми среднеквадратическими отклонениями соответствуют узкие,
вытянутые вверх кривые, а распределениям с большими среднеквадратическими отклонениями
более пологие кривые с менее выраженными вершинами (малые отклонения более вероятны,
большие - менее вероятны);
Правило 3-х сигм
68,25% всех значений лежит в интервале 
±σ (±1 среднеквадратическое отклонение от среднего);
95,44% всех значений лежит в интервале ±2σ (±2 среднеквадратических отклонений от среднего);
99,73% всех значений лежит в интервале ±3σ (±3 среднеквадратических отклонений от среднего).
Пример. Приведены результаты измерения частоты пульса у некурящих студентов-медиков в возрасте 20 лет: 68, 58, 65, 55, 70, 62, 60, 65, 70, 58, 62, 58, 62, 60, 60, 65, 62, 55, 62, 58, 60, 70, 62, 65, 60, 68, 65, 62, 68, 65, 60, 62, 60, 68, 65, 60, 62, 60, 65, 62, 68. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).
Решение. Построим вариационный ряд: 55, 55, 58, 58, 58, 58, 60, 60, 60, 60, 60, 60, 60, 60, 60, 62, 62, 62, 62, 62, 62, 62, 62, 62, 62, 65, 65, 65, 65, 65, 65, 65, 65, 68, 68, 68, 68, 68, 70, 70, 70.
Дискретный статистический ряд распределения
| |||||||
| |||||||
| 
| 
| 
| 
| 
| 
| 
|
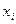
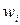
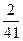
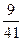
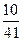
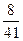
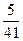
Полигон частот
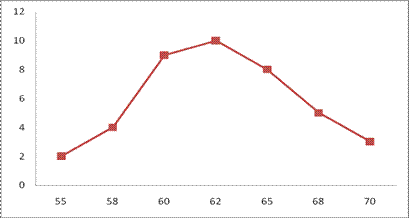
Мода М0=62. Медиана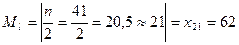 
Выборочная средняя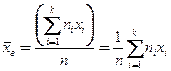 
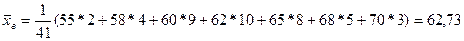– средняя частота пульса у некурящих студентов-медиков.
|
|
Выборочная дисперсия
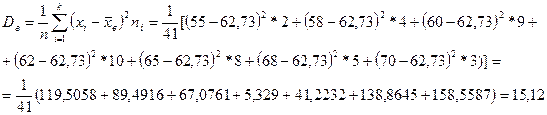
Выборочное среднее квадратическое отклонение: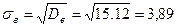 
.
Найдем меру относительного разброса данных: коэффициент вариации
.
Величина коэффициента вариации, равная 6,2%, свидетельствует о слабом разнообразии признака. Таким образом, изучаемую совокупность можно считать однородной.
Величину отклонения выборочного показателя от его генерального параметра называют стандартной ошибкой среднего (нельзя путать со средним квадратичным отклонением изучаемой случайной переменной):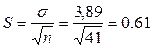 
Доверительный интервал для выборочного среднего значения находится между границами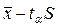 
и 
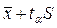, где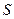 
- стандартная ошибка среднего, 
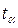- коэффициент Стьюдента, величина, зависящая от объема выборки 
(или соответствующего числа степеней свободы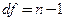 
) и выбранного уровня доверительной вероятности, определяется по таблице распределений Стьюдента.
