Определим количество интервалов по формуле Стерджеса.
Определим величину шага интервала 
.
| Интервалы группировки | 
| 
| 
| 
| 
| 
| 
|
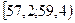
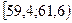
Частоты 
|
Гистограмма частот
Правило 3-х сигм
Ø 68,25% всех значений лежит в интервале 
±σ;
Ø 95,44% всех значений лежит в интервале ±2σ;
Ø 99,73% всех значений лежит в интервале ±3σ.
, т.е. в интервале 
расположено 27 вариант из 41, что составляет 65,85% от объема выборки.
,
.
Согласно этим данным можно сделать вывод, что выборка подчиняется нормальному закону распределения.
Задания
1. Рост 20 мальчиков в возрасте двух лет (в см) равен: 96, 96, 95, 86, 88, 90, 91, 90, 91, 90, 90, 92, 92, 89, 88, 88, 87, 93, 93, 97. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, коэффициент вариации, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).
2. При измерениях в однородных группах обследуемых получены следующие выборки: 12, 14, 12, 13, 14, 15, 14, 14, 12, 14 (частота дыхания). Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, коэффициент вариации, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).
3. Из продукции, произведенной фармацевтической фабрикой за месяц, случайным образом отобраны 15 коробочек некоторого гомеопатического препарата, количество таблеток в которых оказалось равным соответственно 50, 51, 48, 52, 50, 49, 50, 47, 50, 51, 49, 50, 52, 48, 49. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, коэффициент вариации, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).
|
|
Литература
Основная литература
1. Адибаев Б.М. Элементы математической статистики и основы теории верятностей. Учебное пособие, Алматы 2004г.
2. Баврин И.И. Краткий курс высшей математики. Учебник для химико-биологических и медицинских специальностей. Москва. 2003г.
3. Павлушков И.В. Основы высшей математики и математической статистики. Учебник для медицинских и фармацевтических вузов. М., 2003г.
4. Е.А.Лукьянова Медицинская статистика. Москва. Издательство Россиского университета дружбы народов.2002г.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., «Высшая школа», 2002г.
6. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа, 2001г.
7. Морозов В.Ю. Основы высшей математики и статистики. Москва. Медицина. 2001г.
8. Турецкий В.Я. Математика и информатика. Москва. ИНФРА-М. 2004г.
9. Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. Москва. 2001г.
Дополнительная литература
1. Чистяков В.П. Курс теории вероятностей. М., «Наука», 1982г.