Лекция 4. Случайные величины и законы распределения.
| 1.Случайная величина.
Возможный исход любого события можно выразить через функцию от начальных исходных данных или условий. Случайная величина представляет собой переменную, которая может принять одно из возможных значений. Например, количество проданных автомобилей за год или скорость ветра в определенный момент времени. В первом случае случайная величина называется дискретной, во втором - непрерывной. Отсюда можно сформулировать такое определение: случайной величиной Х называется функция, значением которой является определенный исход события на множестве возможных исходов данного события.
Х = f (x)
|
| |
| Для описания случайной величины, используют закон распределения. Законом распределения называется определенное соотношение случайной величины и соответствующей ей вероятности. Закон распределения может быть задан аналитически, в виде таблицы или графически.
Например, вероятность угадывания 5-ти цифр из 36
где
Х - число угаданных цифр Р - соответствующая ей вероятность
 На рисунке 1 изображен полигон распределения вероятностей в виде точек, образующих ломаную кривую. Данный закон распределения задан графически и в виде таблицы.
На рисунке 1 изображен полигон распределения вероятностей в виде точек, образующих ломаную кривую. Данный закон распределения задан графически и в виде таблицы.
|
|  Рис.1 Рис.1
| |
| Так как перечислены все возможные исходы события, то сумма вероятностей всех исходов равна 1.
 Иными словами, закон распределения показывает как распределена случайная величина, т.е. какой вероятностью обладает каждое из значений случайной величины или событий.
Иными словами, закон распределения показывает как распределена случайная величина, т.е. какой вероятностью обладает каждое из значений случайной величины или событий.
|
| | |
2.Функция распределения.
| |
| |
| Не для всех событий можно представить закон распределения в виде ограниченного числа исходов, т.е. значений случайных величин. Существуют события, которые представляют собой непрерывную случайную величину. Например, расход топлива за определенный промежуток времени, расход воды, электроэнергии, скорость ветра, потока и т.д. Закон распределения вероятностей для таких событий представляет собой функцию распределения непрерывной случайной величины. Описать все возможные значения случайной величины для таких событий невозможно, т.к. их количество бесконечно. Для того, чтобы дать количественную характеристику этого распределения, используют функцию распределения случайной величины F (x).
 где Х принимает значения меньшие х.
где Х принимает значения меньшие х.
|
| |
| Функция распределения существует как для прерывных случайных величин, так и непрерывных (Рис. 2 и 3). Из графика видно, что функция прерывной случайной величины - это ступенчатая функция, которая принимает ограниченное число отдельно взятых значений. Непрерывная случайная величина непрерывна в любой точке. Исключением могут быть отдельные точки.
Функция распределения является неубывающей функцией. На минус бесконечности она равна нулю, на плюс бесконечности - единице.
Вероятность отдельного значения непрерывной случайной величины равна нулю.
На ряду с аналитическим, графическим и табличным способами задания случайной величины, существует еще способ задания с помощью плотности вероятности случайной величины, которая существует только для непрерывных случайных величин.
Плотностью вероятности случайной величины называется производная ее функции распределения.
|
| 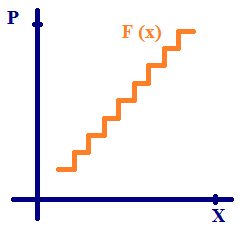 Рис.2 Прерывная случайная величина. Рис.2 Прерывная случайная величина.  Рис.3 Непрерывная случайная величина. Рис.3 Непрерывная случайная величина.
|
| |
| 
|
| |
| Плотность вероятности непрерывной случайной величины обладает следующими свойствами.
Плотность вероятности является неотрицательной функцией.
 Функцию распределения непрерывной случайной величины можно выразить через плотность вероятности по формуле:
Функцию распределения непрерывной случайной величины можно выразить через плотность вероятности по формуле:
 Интеграл, взятый от плотности вероятности в бесконечных пределах, равен единице.
Интеграл, взятый от плотности вероятности в бесконечных пределах, равен единице.
|
|  Рис.4 Рис.4
|
| |
|  Интеграл, взятый от плотности вероятности на определенном промежутке, равен вероятности попадания случайной величины в этот промежуток.
Интеграл, взятый от плотности вероятности на определенном промежутке, равен вероятности попадания случайной величины в этот промежуток.
 Геометрический смысл плотности вероятности заключается в том, что площадь под кривой плотности вероятности равна вероятности распределения случайной величины. (Рис.4 и 5)
Геометрический смысл плотности вероятности заключается в том, что площадь под кривой плотности вероятности равна вероятности распределения случайной величины. (Рис.4 и 5)
|
|  Рис.5 Рис.5
| |
1.Биномиальный закон распределения.
Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.

| | |
| Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.
|
| |
| 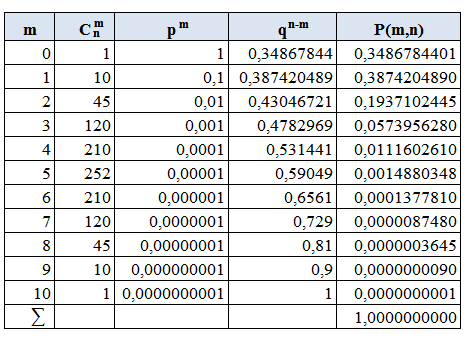 В таблице m - число заказов, полученных компанией на покупку телевизора. Сnm - число сочетаний m телевизоров по n, p - вероятность наступления события А, т.е. заказа телевизора, q - вероятность не наступления события А, т.е. не заказа телевизора, P m,n - вероятность заказа m телевизоров из n.
На рисунке 1 изображен полигон распределения вероятностей.
В таблице m - число заказов, полученных компанией на покупку телевизора. Сnm - число сочетаний m телевизоров по n, p - вероятность наступления события А, т.е. заказа телевизора, q - вероятность не наступления события А, т.е. не заказа телевизора, P m,n - вероятность заказа m телевизоров из n.
На рисунке 1 изображен полигон распределения вероятностей. 
| | Рис.1
|
| |
| | | | | | | | |
| 2.Геометрическое распределение.
|
| |
| Геометрическое распределение случайной величины имеет следующий вид:
 где
Pm - вероятность наступления события А в испытание под номером m. р - вероятность наступления события А в одном испытании. q = 1 - p
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
где
Pm - вероятность наступления события А в испытание под номером m. р - вероятность наступления события А в одном испытании. q = 1 - p
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
|
| |
| 
|
|  Рис.2 Рис.2
|
| |
| Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 - что десятый блок оказался неисправным - 0,038742049, 2 - что все проверяемые блоки оказались исправными - 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события Pm (10 проверенных блоков) относительно высокая. Рис.2.
|
| | | 3.Гипергеометрическое распределение.
|
|
| |
| Гипергеометрическое распределение случайной величины имеет следующий вид:
 где
где
 Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M - всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m - число правильно угаданных чисел среди изъятых.
Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M - всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m - число правильно угаданных чисел среди изъятых.
|
| |
| 
|
|  Рис.3 Рис.3
|
| |
| Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.
|
| | | 4.Закон распределения Пуассона.
|
|
| |
| Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:
 где
λ = np = const n - число испытаний, стремящиеся к бесконечности p - вероятность наступления события, стремящаяся к нулю m - число появлений события А
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 (≤10)
где
λ = np = const n - число испытаний, стремящиеся к бесконечности p - вероятность наступления события, стремящаяся к нулю m - число появлений события А
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 (≤10)
|
| |
|  (таблица дана не полностью)
(таблица дана не полностью)
|  Рис.4 Рис.4
| |
| Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)
|
| |
| Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.
|
| | | 5.Равномерный закон распределения.
|
|
| |
| Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.
|
| |
| 
|
|  Рис.5 Рис.5
|
| | | 6.Нормальный закон распределения (закон Гаусса).
|
| |
| Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:
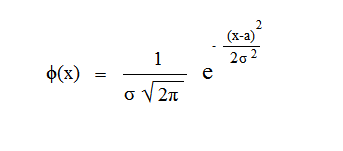 где а - математическое ожидание случайной величины σ - среднее квадратическое отклонение
где а - математическое ожидание случайной величины σ - среднее квадратическое отклонение
|
| |
| График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:
 При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
|
|  Рис.6 Рис.6
|
| |
| Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:

|
|  Рис.7 Рис.7
|
| |
| Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть - от а до х. (Рис.7)
|
| | | 7.Показательный закон распределения.
|
| |
| Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид:
 где λ - параметр обратно-пропорциональный математическому ожиданию.
График плотности вероятности с параметрами λ = 2, λ = 4, λ =6 изображен на рис.8
где λ - параметр обратно-пропорциональный математическому ожиданию.
График плотности вероятности с параметрами λ = 2, λ = 4, λ =6 изображен на рис.8
|
|  Рис.8 Рис.8
|
| |
| Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид:
 График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:

|
|  Рис.9 Рис.9
|
| | | 8.Логарифмически-нормальное распределение.
|
| |
| Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид.
|
| |
| 
|
|  Рис.10 Рис.10
|
| |
| Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)
|
| | | 9. χ ² распределение
|
| |
| Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением.
χ ² распределение имеет вид:
 где
Аi - i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,...k).
где
Аi - i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,...k).
|
| |
| Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:

|
|  Рис.11 Рис.11
|
| |
|
Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.
|
| | | 10.Распределение Стьюдента (t - распределение)
|
| |
| Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид:
 где
Z - случайная величина, распределенная по нормальному закону. χ ² - случайная величина, имеющая χ ² - распределение с k степенями свободы.
где
Z - случайная величина, распределенная по нормальному закону. χ ² - случайная величина, имеющая χ ² - распределение с k степенями свободы.
|
| |
| Плотность вероятности распределения Стьюдента имеет вид:

|
|  Рис.12 Рис.12
|
| |
| На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.
|
| | | 11. Распределение Фишера-Снедекора.
|
|
| |
| Распределение случайной величины Фишера-Снедекора имеет вид:

|
| |
| Плотность вероятности случайной величины имеет вид:

|
|  Рис.13 Рис.13
|
| |
| При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)
| |
|
Поиск по сайту:
|
 На рисунке 1 изображен полигон распределения вероятностей в виде точек, образующих ломаную кривую. Данный закон распределения задан графически и в виде таблицы.
На рисунке 1 изображен полигон распределения вероятностей в виде точек, образующих ломаную кривую. Данный закон распределения задан графически и в виде таблицы.
 Рис.1
Рис.1
 Иными словами, закон распределения показывает как распределена случайная величина, т.е. какой вероятностью обладает каждое из значений случайной величины или событий.
Иными словами, закон распределения показывает как распределена случайная величина, т.е. какой вероятностью обладает каждое из значений случайной величины или событий.
 где Х принимает значения меньшие х.
где Х принимает значения меньшие х.
 Рис.2 Прерывная случайная величина.
Рис.2 Прерывная случайная величина.  Рис.3 Непрерывная случайная величина.
Рис.3 Непрерывная случайная величина.

 Функцию распределения непрерывной случайной величины можно выразить через плотность вероятности по формуле:
Функцию распределения непрерывной случайной величины можно выразить через плотность вероятности по формуле:
 Интеграл, взятый от плотности вероятности в бесконечных пределах, равен единице.
Интеграл, взятый от плотности вероятности в бесконечных пределах, равен единице.
 Рис.4
Рис.4
 Интеграл, взятый от плотности вероятности на определенном промежутке, равен вероятности попадания случайной величины в этот промежуток.
Интеграл, взятый от плотности вероятности на определенном промежутке, равен вероятности попадания случайной величины в этот промежуток.
 Геометрический смысл плотности вероятности заключается в том, что площадь под кривой плотности вероятности равна вероятности распределения случайной величины. (Рис.4 и 5)
Геометрический смысл плотности вероятности заключается в том, что площадь под кривой плотности вероятности равна вероятности распределения случайной величины. (Рис.4 и 5)
 Рис.5
Рис.5

 В таблице m - число заказов, полученных компанией на покупку телевизора. Сnm - число сочетаний m телевизоров по n, p - вероятность наступления события А, т.е. заказа телевизора, q - вероятность не наступления события А, т.е. не заказа телевизора, P m,n - вероятность заказа m телевизоров из n.
На рисунке 1 изображен полигон распределения вероятностей.
В таблице m - число заказов, полученных компанией на покупку телевизора. Сnm - число сочетаний m телевизоров по n, p - вероятность наступления события А, т.е. заказа телевизора, q - вероятность не наступления события А, т.е. не заказа телевизора, P m,n - вероятность заказа m телевизоров из n.
На рисунке 1 изображен полигон распределения вероятностей. 
 где
Pm - вероятность наступления события А в испытание под номером m. р - вероятность наступления события А в одном испытании. q = 1 - p
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
где
Pm - вероятность наступления события А в испытание под номером m. р - вероятность наступления события А в одном испытании. q = 1 - p
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.

 Рис.2
Рис.2
 где
где
 Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M - всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m - число правильно угаданных чисел среди изъятых.
Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M - всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m - число правильно угаданных чисел среди изъятых.

 Рис.3
Рис.3
 где
λ = np = const n - число испытаний, стремящиеся к бесконечности p - вероятность наступления события, стремящаяся к нулю m - число появлений события А
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 (≤10)
где
λ = np = const n - число испытаний, стремящиеся к бесконечности p - вероятность наступления события, стремящаяся к нулю m - число появлений события А
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 (≤10)
 (таблица дана не полностью)
(таблица дана не полностью)
 Рис.4
Рис.4

 Рис.5
Рис.5
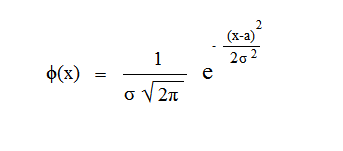 где а - математическое ожидание случайной величины σ - среднее квадратическое отклонение
где а - математическое ожидание случайной величины σ - среднее квадратическое отклонение
 При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
 Рис.6
Рис.6

 Рис.7
Рис.7
 где λ - параметр обратно-пропорциональный математическому ожиданию.
График плотности вероятности с параметрами λ = 2, λ = 4, λ =6 изображен на рис.8
где λ - параметр обратно-пропорциональный математическому ожиданию.
График плотности вероятности с параметрами λ = 2, λ = 4, λ =6 изображен на рис.8
 Рис.8
Рис.8
 График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:

 Рис.9
Рис.9

 Рис.10
Рис.10
 где
Аi - i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,...k).
где
Аi - i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,...k).

 Рис.11
Рис.11
 где
Z - случайная величина, распределенная по нормальному закону. χ ² - случайная величина, имеющая χ ² - распределение с k степенями свободы.
где
Z - случайная величина, распределенная по нормальному закону. χ ² - случайная величина, имеющая χ ² - распределение с k степенями свободы.

 Рис.12
Рис.12


 Рис.13
Рис.13