Лабораторная задача QM-6
Движение частицы в поле прямоугольного потенциала.
Краткая теория.
Стационарное решение.
Пусть частица, движущаяся слева направо, падает на потенциальный барьер или потенциальную яму высоты U0 (рис. 5.1). По классическим представлениям если энергия частицы E больше высоты барьера частица беспрепятственно проходит над барьером, если же E<U0, как показано на рис. 6.1, то частица отражается от барьера и движется в обратную сторону. В первом случае вероятность прохождения D = 1, а вероят-ность отражения R = 0. Во втором случае D=0, а R =1.
 |
Совершенно иначе выглядит поведение частицы в квантовой механике. Во-первых, даже при E>U0 частица может отразиться от барьера и поле-теть в обратную сторону. Во-вторых, при E<U0 имеется отличная от нуля вероятность того, что частица проникнет через барьер и окажется в области Ш. Такое, совершенно невозможное с точки зрения классиче-ской механики, поведение микрочастицы следует из уравнения Шредингера. Будем предполагать, что на препятствие падает поток час-
тиц с фиксированной энергией. При этом коэффициент отражения опре-
деляется как отношение отраженного от препятствия потока к падающ-ему. Очевидно, случай U0<0 соответствует потенциальной яме, а U0>0
- барьеру. При этом, если E>U0, то говорят о надбарьерном движении частицы, а при E<U0 – о ее туннелировании через потенциальный барьер.
Рассмотрим решение уравнения Шредингера, которое для областей
I и III запишется в виде (6.1), а для области II в виде (6.2):

 (6.1)
(6.1)
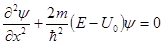 .
.  (6.2).
(6.2).
Обозначив 
 и
и  , получим:
, получим:

ψ΄΄ + k2ψ = 0, (6.3)
ψ΄΄ + χ2ψ = 0. (6.4)
Решение уравнения (6.3) для областей I и III имеет вид:
ψ1,3(x) = A1,3 e-ikx + B1,3 eikx (6.5)
Решение уравнения (6.4) для области II имеет вид: 
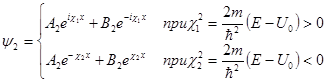 (6.6)
(6.6)
Коэффициенты уравнений (6.5) и (6.6) находятся из условия непрерывности волновых функций: на границе соприкасающихся областей волновые функ-
ции и их производные должны быть равны (условие “сшивания” волновых
функций). Произведя “сшивание” волновых функций и их первых производ-
ных в точках разрыва потенциала, а также полагая В3 = 0 (т. е. считая, что
отсутствует волна, падающая на барьер справа) после несложных преобразо-
ваний получим следующие выражения для коэффициента прохождения:
 , при E<U0 (6.7)
, при E<U0 (6.7)
 , при E>U0 (6.8)
, при E>U0 (6.8)
Как видно, выражение (6.7) определяет вероятность туннелирования, а
(6.8) описывает прохождение частиц над потенциальным барьером (ямой).

Естественно, что D + R=1, где R – вероятность отражения частицы.Проа-нализируем полученные выражения. Рассмотрим сначала случай E<U0. В классической механике частицы, падающие на такой потенциальный барьер, целиком отразились бы, то есть D = 0. В квантовой механике прозрачность D барьера не равна нулю и рассчитывается по формуле (6.7), а для случая
достаточно больших значений χ2a (когда можно в выражении sh2 χ2a
можно пренебречь величиной  по сравнению с
по сравнению с  ) равна:
) равна:

 (6.9)
(6.9)
Перейдем к анализу выражения (6.8), полученному для случая E>U0.
В классической механике должно бы быть D =1. Из формулы (6.8) следует,
что прозрачность D близка к единице только при условии:
χ2 a = n π, n = 1,2,3,… (6.10)
Полученные результаты позволяют понять природу целого ряда явлений в
физике микромира, которые не могут быть объяснены в рамках классичес-кой теории. Прежде всего это относится к α- распаду тяжелых атомных ядер
и холодной эмиссии электронов с поверхности металлов,помещенных в дос-
таточно сильное электрическое поле. Эти явления в квантовой механике мо-
гут быть объяснены туннелированием α- частиц через потенциальный барь-ер, удерживающий их в ядре, и туннелированием электронов через барьер,
возникающий при помещении металлов в сильное электрическое поле.
Квантовая механика объясняет и эффект Рамзауэра – глубокий минимум ве-
личины сечения упругого рассеяния электронов на атомах тяжелых инертных газов. С точки зрения квантовой механики минимум Рамзауэра
связан с тем, что при определенных энергиях электрона на размере области
действия атомного потенциала укладывается целое число полуволн де Брой-
ля, в результате чего такие электроны проходят атом без рассеяния.
Рассмотренная стационарная теория не позволяет тем не менее рас-смотреть реальную пространственно-временную картину движения части-цы через потенциальный барьер, которая является существенно нестацио-нарной. Поэтому представляет значительный интерес рассмотреть постав-ленную задачу на основе нестационарного уравнения Шредингера. Такое рассмотрение позволяет получить ответы на ряд вопросов, представля-ющих значительный практический интерес (например, длительность про-цесса туннелирования, скорости прошедших и отраженных частиц и т.д.).
Данная задача сложна и не может быть решена аналитически. В работе [3] приведено численное решение нестационарного уравнения Шредингера для потенциального барьера. Предполагается, что начальное
состояние частицы задается пакетом гауссовой формы с полушириной Dx, движущимся по направлению области действия потенциала со средней скоростью  :
:
 (6.11)
(6.11)
Типичная временная картина туннелирования такого пакета через потенциальный барьер произвольной формы высоты U0 и ширины a представлена на рисунках 6.2 и 6.3. Как видно, пакет по мере приближения к области действия потенциала постепенно расплывается, но сохраняет свою форму. При попадании пакета в область действия потенциала его форма нарушается в результате формирования отраженного волнового пакета и его интерференции с падающим на препятствие пакетом. Через некоторое время формируются два пакета: отраженный и прошедший через препятствие. При этом значения коэффициентов D и R могут быть вычислены как
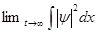 ,
,
где интеграл берется по области классически разрешенного движения справа и слева от потенциала соответственно. Следует обратить внимание на то,
 |
что речь идет о движении единственной частицы, которая при определении ее координат оказывается локализованной в конкретной точке пространства, а величина  определяет именно распределение вероятности ее обнаруже-ния в различных точках пространства. Существенно также отметить, что отраженный волновой пакет “отстает” от отраженной от барьера классичес-кой частицы. Физически это связано с тем, что пакет частично проникает в область U0 > E (
определяет именно распределение вероятности ее обнаруже-ния в различных точках пространства. Существенно также отметить, что отраженный волновой пакет “отстает” от отраженной от барьера классичес-кой частицы. Физически это связано с тем, что пакет частично проникает в область U0 > E ( ), в то время как в классическом случае отражение происходит строго в точке скачка потенциала.
), в то время как в классическом случае отражение происходит строго в точке скачка потенциала.
В каком случае представленная квантомеханическая картина совпадает с классической? Конечно, для этого необходимо чтобы прозрачность барьера была мала, то есть  , где
, где  . Однако это условие является необходимым, но не достаточным, так как при
. Однако это условие является необходимым, но не достаточным, так как при  (то есть для “низкого” на боль-
(то есть для “низкого” на боль-
шой протяженности потенциала) области отражения частицы с квантовой
и классической точек зрения окажутся различными, что приведет к запаз-дыванию пакета по сравнению с классической материальной точкой.
В качестве еще одного примера рассмотрим результаты решения задачи о движении пакета через потенциальный барьер. При указанных параметрах картина наблюдаемого процесса оказывается более сложной чем в предыдущем случае. С некоторой вероятностью происходит как бы “застревание” частицы в области действия потенциала, что приводит к формированию сразу нескольких пакетов, как отраженных от препятствия, так и прошедших через него. При этом положение классической материальной точки вообще говоря может не совпадать не с одним из пакетов.
В каком соотношении находятся описанные стационарный и не- стационарный подходы с точки зрения определения величин D и R? Нестационарный подход богаче по своим возможностям. Действительно, задавая начальное состояние системы, например в виде гауссового пакета ширины а, движущегося в сторону области действия потенциала, мы не знаем точного значения импульса и энергии этой частицы. Поэтому возникает вопрос о зависимости коэффициентов D и R от степени локализации частицы в начальном состоянии. Результаты, полученные в рамках стационарного и нестационарного подходов, совпадут лишь в предельном случае сильно нелокализованного начального состояния, когда неопределенности импульса и энергии частицы окажутся несущественными.
Описание программы
Программа Infinite movement in the rectangular potential богата по своим возможностям и предоставляет широкий выбор для экспериментирования.
В меню лабораторной задачи (рис. 6.4) вы должны задать начальное состо-
яние частицы (величины энергии E0 и начальной ширины волнового пакета
x0), а также параметры потенциала. В программе используется потенциал
 |
прямоугольной формы, характеризуемый двумя параметрами: шириной d
и высотой U0. При этом случай U0>0 соответствует потенциальному барь-
еру, а случай U0<0 – потенциальной яме. При изучении рассеяния на по-
тенциальном барьере можно рассмотреть как случай U0> E0 (туннели-рование частицы через барьер), так и U0< E0 – надбарьерное движение
частицы). При изучении туннельного эффекта следует иметь в виду, что
его вероятность экспоненциально быстро убывает с шириной и высотой барьера. Поэтому для наблюдения прошедшего через барьер пакета ши-
рина барьера должна быть достаточно мала. В программе при нажатии клавиши F1 предусмотрена возможность вычисления вероятностей веро-
ятностей проникновения частицы через потенциальный барьер (trans-missivity) и отражения ее от барьера (reflectivity). Поэтому вы можете
проанализировать зависимости вероятности туннелирования от параметров
потенциала и начального состояния частицы. Такие же зависимости можно
получить и для надбарьерного движения частицы и для рассеяния на потен-
циальной яме. Коэффициенты отражения и прохождения определяются в
программе как вероятности обнаружить частицу справа и слева от потенци-
альной ямы. Поэтому величина 1 - (D + R) дает вероятность пребывания
частицы в области действия потенциала. В области достаточно больших вре-
мен получается естественный результат D + R →1. В данной программе
целесообразно использовать большее пространственное разрешение, напри-
мер, установить разрешение, равное 3. Это позволит существенно увеличить размер области счета и более полно увидеть нестационарную картину рас-сеяния. Можно также проследить за движением классической частицы и увидеть принципиально различные результаты квантового и классического рассмотрения.
Порядок выполнения работы.
Упражнение 1. Туннелирование электрона.
1. Установите в меню лабораторной задачи пространственное разрешение
(Space Resolution), равное 3, энергию электрона (Energy) и начальную
ширину (Width) волнового пакета – 35 эВ и 1Å соответственно и пара-
метры потенциального барьера: ширину d (Potential Width) и высоту
U0 (Potential Depth), равными 4Å и 40 эВ соответственно. Наблюдай-
те на экране терминала картину туннелирования электрона. По окончании
процесса запишите значения энергии E0, вероятности прохождения D и
вероятности отражения R частицы от барьера.
2. Проведите измерения (пункт 1) при других значениях E0, меньших
U0. Рекомендуется выбрать E0=30, 25, 20, 15, 10 эВ. Сравните харак-
тер движения классической и квантовой частиц. Отпечатайте наиболее
характерную картину туннелирования.
3. Постройте график зависимости  . Убедитесь, что
. Убедитесь, что
построенный график соответствует формуле прозрачности потенциальн-
ого барьера.
Упражнение 2. Надбарьерное движение электрона.
1. Установите в меню лабораторной задачи пространственное разрешение
(Space Resolution), равное 3, энергию электрона (Energy) и начальную
ширину (Width) волнового пакета – 36 эВ и 1Å соответственно и пара-
метры потенциального барьера: ширину (Potential Width) и высоту
(Potential Depth), равными 10 Å и 30 эВ соответственно. Наблюдайте
на экране терминала картину движения электрона. В момент, когда клас-
сическая частица закончит свое движение над барьером (при этом резко
увеличится скорость движения частицы), клавишей F1 остановите про-
цесс. По окончании процесса запишите значения вероятности прохожде-
ния барьера D и значения E0, U0 и d.
2. Проведите измерения (пункт 1) при других значениях ширины потен-
циального барьера d. Рекомендуется выбрать значения 9, 8, 7, 6, 5, 4,
3, 2 и 1.5Å. Постройте график зависимости D=f(d). Обратите внима-
ние на максимумы и минимумы этой зависимости. Рассчитайте длину
волны де Бройля электрона по формуле 

и сопоставьте положение максимумов функции D=f(d) с длиной вол-
ны электрона (смотри формулу (6.10)).
Упражнение 3. Рассеяние электронов потенциальной ямой.
1. Установите в меню лабораторной задачи пространственное разрешение
, равное 3, энергию электрона и начальную ширину волнового пакета –
40 эВ и 2Å соответственно и параметры потенциального барьера: шири-
нуи высоту, равными 10 Å и - 180 эВ соответственно. Наблюдайте
на экране терминала картину движения электрона. Отпечатайте наиболее
характерную картину рассеяния электронных волн.
2. Проведите наблюдения (пункт 1) при других значениях ширины потен-
циальной ямы и энергии электрона.
Контрольные вопросы.
1. Запишите стационарное уравнение Шредингера для областей I, II и III
потенциального поля, изображенного на рис. 6.1.
2. В чем заключается "сшивание" волновых функций на границе соприка-
сающихся областей потенциального поля?
3. Напишите формулы прозрачности D потенциального барьера и коэф-
фициента отражения частицы от барьера R, полученные из стационар-
ных решений.
4. Почему сумма полученных в упражнении 1 значений D и R не равна
единице?
5. В чем заключается эффект Рамзауэра? Подтверждают ли результаты,
полученные в упражнении 2 этот эффект?
6. Чем можно объяснить недостаточную резкость максимумов функции
D=f(d), изученной вами в упражнении 2?
7. Чем отличается движение классической частицы от движения
волнового пакета при рассеянии частиц потенциальной ямой?