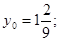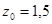Вычислить тройной интеграл: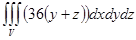 
;
V: 
Решение:
Перейдем от тройного интеграла к повторному:
= 
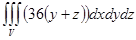Проведем поэтапное вычисление интеграла:
) 
) 
=
=
) 
= 
= 
) 
Ответ: 12,5
Приложения двойных интегралов
) Площадь плоской фигуры 
:
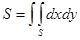
) Объем тела, ограниченного поверхностями:
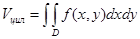
)Площадь части криволинейной поверхности:
) Момент инерции относительно начала координат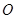 
плоской фигуры 
:
) Масса плоской фигуры 
переменной поверхностной плотности
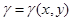
Рассмотрим приложения двойных интегралов на конкретных задачах.
Пример 1
Найти площадь фигуры, ограниченной данными линиями: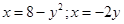 
.
Решение:
Зададим область D неравенствами:
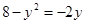D: 
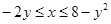
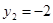
Вычислим двойной интеграл
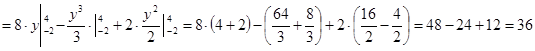
Ответ: S=36
Пример 2
Найти объем тела, ограниченного данными поверхностями: 
Решение:
Зададим область D неравенствами:
D: 
Перейдем от двойного интеграла к повторному.
= 
.
Проведем поэтапное вычисление интеграла.
) 
2) 
Ответ: 
Пример 3
Найти площадь части конуса 
, заключенной внутри цилиндра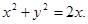 
Решение:
Зададим область D неравенствами в полярных координатах:
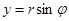
D: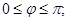 
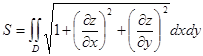
Найдем частные производные:
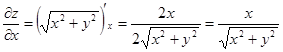
Перейдем к полярным координатам и заменим двойной интеграл повторным:
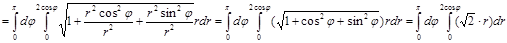
Проведем поэтапное вычисление интеграла:
) 
2) 
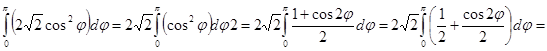
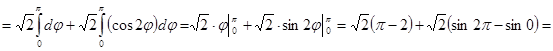
Ответ: 
Пример 4
Найти момент инерции фигуры, заданной неравенствами: 
относительно начала координат, если его плотность постоянна и равна 3.
Решение:
Зададим область D неравенствами:
, 
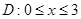Перейдем от двойного интеграла к повторному:
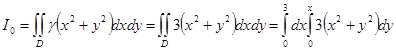
Проведем поэтапное вычисление интеграла:
) 
2) 
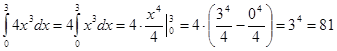
Ответ: 
Пример 5
Найти массу плоской фигуры, заданной неравенствами: 
с переменной поверхностной плотностью: 
.
Решение:
Перейдем от двойного интеграла к повторному:
.
Проведем поэтапное вычисление интеграла:
) 
) 
Ответ: 
Приложения тройных интегралов
кратный интеграл инерция статистический
1) Объем тела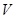 
:
) Масса тела 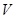плотности:
) Моменты инерции тела 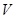относительно координатных осей и начала координат:
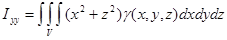
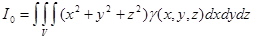
) Статистические моменты тела относительно координатных плоскостей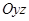 
, 
, 
:
5) Координаты центра масс тела:
Рассмотрим приложения тройных интегралов на конкретных задачах.
Пример 1
Найти объем тела, ограниченного плоскостями 
Решение:
Зададим область 
неравенствами:
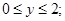
Перейдем от тройного интеграла к повторному:
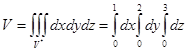
Проведем поэтапное вычисление интеграла:
) 
2) 
3) 
Ответ: 
Пример 2
Найти массу тела, ограниченного плоскостями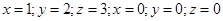 
плотности 
Решение:
Зададим область неравенствами:
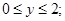
Перейдем от тройного интеграла к повторному:
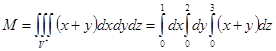
Выполним поэтапное вычисление интеграла:
) 
) 
=
) 
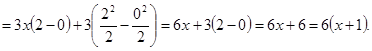
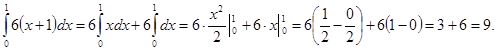
Ответ: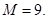 
Пример 3
Найдите моменты инерции тела, ограниченного плоскостями 
и плотностью 
относительно координатных осей и начала координат.
Решение:
Зададим область V неравенствами:
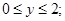
Найдем момент инерции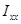 
.
Перейдем от тройного интеграла к повторному:
Проведем поэтапное вычисление интеграла:
) 
2) 
=
) 
Найдем момент инерции 
.
Перейдем от тройного интеграла к повторному:
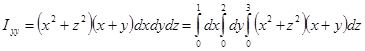
Проведем поэтапное вычисление интеграла:
) 
) 
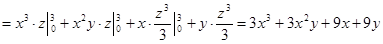
3) 
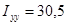
Найдем момент инерции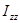 
.
Перейдем от тройного интеграла к повторному:
Проведем поэтапное вычисление интеграла:
1) 
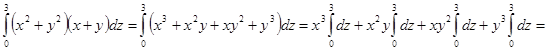
2) 
) 
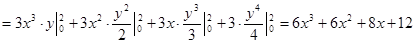
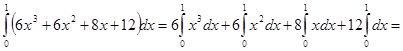
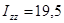
Найдем момент инерции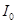 
.
Перейдем от тройного интеграла к повторному:
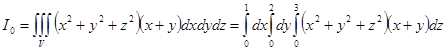
Проведем поэтапное вычисление интеграла:
) 
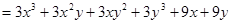
2) 
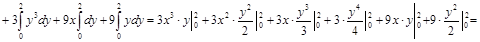
3) 
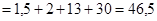
Ответ: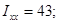 
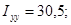
Пример 4
Найти статистические моменты тела, ограниченного плоскостями 
и плотностью относительно координатных плоскостей 
, 
, .
Решение:
Зададим область V неравенствами:
Найдем статистический момент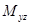 
.
Перейдем от тройного интеграла к повторному:
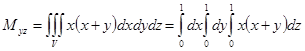
Проведем поэтапное вычисление интеграла:
1) 
2) 
3) 
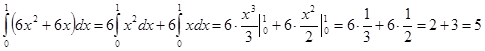
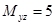
Найдем статистический момент 
.
Перейдем от тройного интеграла к повторному:
Проведем поэтапное вычисление интеграла:
) 
2) 
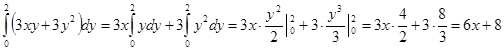
3) 
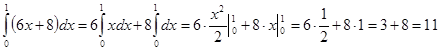
Найдем статистический момент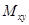 
.
Перейдем от тройного интеграла к повторному:
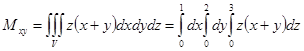
Проведем поэтапное вычисление интеграла:
) 
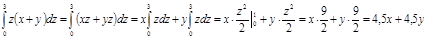
2) 
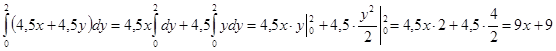
3) 
Ответ: 
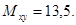
Пример 5
Найти координаты центра масс тела, ограниченного плоскостями и плотностью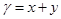 
.
Решение:
Из примера 4:
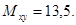
Из примера 2: 
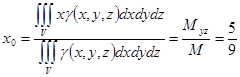
Ответ: 
