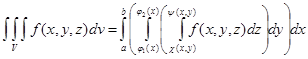Содержание
Введение
. Двойные интегралы
. Тройные интегралы
. Приложения двойных интегралов
. Приложения тройных интегралов
. Контрольная работа по теме: «Приложения кратных интегралов»
Ответы к контрольной работе
Демонстрационные варианты контрольной работы с решениями
Заключение
Список литературы
Введение
Интегрирование прослеживается еще в древнем Египте примерно в 1800 г до н.э. Математический папирус демонстрирует знание формулы объема усеченной пирамиды. Первым известным методом для расчета интегралов является метод исчерпывания Евдокса (примерно 370 г до н.э.), который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны.
Следующий крупный шаг в исчислении интегралов был сделан в Ираке в 11 веке математиком Ибн ал-Хайсамом. В своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла.
Следующий значительный прогресс в исчислении интегралов появится лишь в 16 веке. В работах Кавальери с его методом неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале 17 века Барроу и Торричелли, которые представили первые намеки на связь между интегрированием и дифференцированием.
Работа состоит из введения, теоретической части, состоящей из четырех пунктов, практической части, заключения и списка используемой литературы.
В первой части рассматривается и вводится понятие двойного интеграла, во второй части - понятие тройного интеграла. В третьей и четвертой частях рассматриваются приложения кратных интегралов.
Область исследования - математический анализ
Объект исследования - теория кратных интегралов
Предмет исследования - двойные и тройные интегралы
Проблема исследования - применение кратных интегралов
Методы исследования - изучение литературы, сравнение, обобщение, аналогия, анализ и классификация информации
Цель исследования - изучить теорию кратных интегралов и разработать варианты контрольной работы по теме «Приложения кратных интегралов»
Задачи исследования:
раскрыть понятия «двойной интеграл», «тройной интеграл».
рассмотреть некоторые приложения кратных интегралов
показать примеры вычисления кратных интегралов
рассмотреть применение кратных интегралов для вычисления объема, массы, площади, моментов инерции, статистических моментов и координат центра масс тела на конкретных примерах.
самостоятельно разработать варианты контрольной работы по теме «Приложения кратных интегралов».
Двойные интегралы
Рассмотрим в плоскости 
замкнутую область 
, ограниченную линией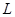 
.
Разобьем эту область какими-нибудь линиями на n частей 
, а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим 
. Выберем в каждой части 
точку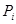 
. Пусть в области D задана функция 
. Обозначим через 
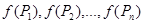значения этой функции в выбранных точках и составим сумму произведений вида: 
: 
, называемую интегральной суммой для функции 
в области .
Если существует один и тот же предел интегральных сумм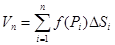 
при 
и 
, не зависящий ни от способа разбиения области на части, ни от выбора точек 
в них, то он называется двойным интегралом от функции по области и обозначается:
Вычисление двойного интеграла по области , ограниченной линиями: 
, 
где 
и 
непрерывному на 
, сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:
Пример вычисления двойного интеграла
Вычислить двойной интеграл: 
; D: 
Решение:
Зададим область D неравенствами:
D: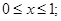 
Перейдем от двойного интеграла к повторному:
= 
Проведем поэтапное вычисление интеграла:
) 
=
= 
) 
= 
=
= 
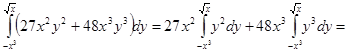
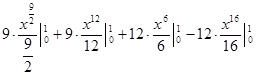Ответ: 4
Тройные интегралы
Понятие тройного интеграла вводится по аналогии с двойным интегралом.
Пусть в пространстве задана некоторая область 
, ограниченная замкнутой поверхностью 
. Зададим в этой замкнутой области непрерывную функцию 
. Затем разобьем область на произвольные части 
, считая объем каждой части равным , и составим интегральную сумму вида: 
Предел при 
интегральных сумм, не зависящий от способа разбиения области и выбора точек 
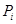в каждой подобласти этой области, называется тройным интегралом от функции 
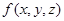по области :
Тройной интеграл от функции 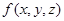по области равен трехкратному интегралу по той же области:
