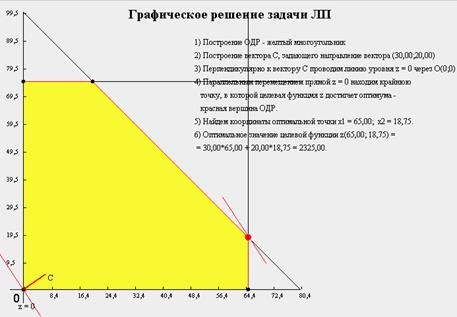
Задача
Получение графического решения оптимального решения математической модели заданной задачи и исследование модели на чувствительность.
Предприятие электронной промышленности выпускает 2 модели радиоприёмников, причём каждая модель производится на отдельной технологической линии.
Суточный объем производства первой линии – 60 изделий; второй линии – 75 изделий.
На радиоприёмник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов.
Максимальный суточный запас используемых элементов равен 800 единицам. Прибыли от реализации одного радиоприемника первой и второй моделей равны 30 и 20 у. е. соответственно.
Определить оптимальные суточные объемы производства первой и второй моделей. Исследовать модель на чувствительность.
Решение
ЛИНЕЙНАЯ МОДЕЛЬ
Статистическое определение: Переменная величина у считается линейной (или линейной функцией) в зависимости от переменных.
Мнение о том, считается ли функция линейной или нет, может меняться в зависимости от того контекста, в котором она применяется.
МОДЕЛЬ
1) совокупность логических, математических или иных соотношений, отображающих с необходимым или возможным приближением к действительности определенные характеристики и параметры изучаемой системы;
2) логическое или математическое описание всех существенных свойств моделируемого объекта. Изучают экономические процессы (ценообразование, механизмы управления и др.), эксперимент. Используют для моделирования взаимосвязей между различными процессами, которые трудно, невозможно или дорого воспроизвести др. средствами и методами.
|
|
ПАРАМЕТРЫ
Величины, описывающие систему переменные в процессе ее функционирования; в конкретных случаях (ситуациях) принимаются постоянными
Линейное программирование - количественный анализ для оптимизации целевой функции, при данном ряде ограничений. Название подразумевает, что функции должны быть линейными.
Проблемы, которые необходимо решить формулируются в задании. Ниже приведен контрольный список вопросов для минимизации риска ошибок в формулировке задания.
1. Любое число в задании должно быть или использовано, или игнорировано.
2. Не забывайте начальных условий.
3. Каждая переменная в целевой функции должна быть перечислена где-нибудь в ограничениях.
4. Необходимо перечислить любые ограничения.
При моделировании проблем функциями, необходимо помнить, что в реальном мире есть изменение. Чувствительный анализ проводится для того, чтобы определить чувствительность решения к изменениям в параметрах.
Примером может быть доход от деятельности предприятия, а планом действий в данном случае может быть производственная программа предприятия.
С точки зрения математики производственную программу предприятия в первом приближении можно записать как набор чисел х1,х2,…,хn котором хi обозначает запланированный выпуск изделий i-го типа, n — количество типов изделий.
Если Ci — доход от произведенного изделия i-го типа и каждое произведенное изделие покупается по одной и той же цене, то суммарный доход предприятия является простой суммой]
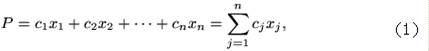
х1 – запланированный выпуск радиоприёмников первой модели
|
|
х2 – запланированный выпуск радиоприёмников второй модели
Другим неотьемлимым элементом экономической ситуации являются ограничения, налагаемые на возможные варианты планов производства.
Чаще всего это так называемые ресурсные ограничения, описывающие тот факт, что для производства товаров приходиться тратить ресурсы;
количество ресурсов, которое можно затратить на производство
товаров, ограничено.
Если считать, что в нашем производстве используются ресурсы i=1,2,…,n, то в модели линейного программирования эти два факта описываются с помощью коэффициентов aij, которые задают затраты i-го ресурса на производство единицы j –го продукта.
Если затраты ресурсов линейно возрастают в зависимости от роста объемов производства, то для выпуска продукта j в количестве xj единиц aijxj i-го ресурса. Выпуск всего плана x = (Х1,Х2,...,хn) потребует при этом

единиц i-го ресурса.
Когда в наличии имеется не более bi единиц этого ресурса, то ясно, что любой реализуемый план производства x должен удовлетворять ограничению
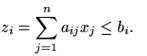
Ограничения по условию задачи:
1) 10х1 + 8х2 ≤ 800
2) х1 ≤ 60
3) х2 ≤ 75
4) х1 >=0
5) х2 >=0
Целевая функция:
z =30х1 + 20х2
В приведенном выше примере естественным экономическим требованием является максимизация дохода предприятия, что будет записываться как

Максимум дохода достигается за счет оптимального выбора производственной программы.
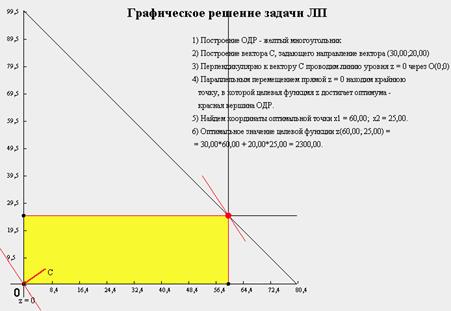
Из этих условий строим графически область допустимых решений (ОДР).
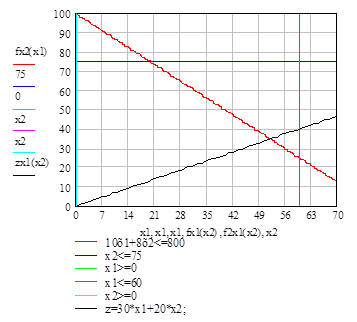
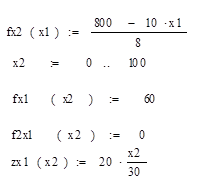
По виду целевой функции определяем вектор нормали, относительно которого ищем оптимальный объём производства радиоприёмников.
|
|
Х1 = 60 изделий.
Х2 = (800 – 10*60)/8 = 25 изделий.
Общая прибыль составляет
Р = 60*30 + 25*20 = 2300 у.е.
Исследование модели на чувствительность
Цель анализа чувствительности - оценить предельное возрастание дефицитного ресурса, ведущее к росту прибыли.
Если задача разрешима, то, кроме данного случая единственного решения, задача может иметь бесконечное множество решений - альтернативный оптимум. В этом случае прямая, соответствующая целевой функции, параллельна прямой, соответствующей одному из связывающих ограничений. Ограничение называют связывающим, если прямая, его представляющая, проходит через оптимальную точку.
Поскольку решение связано с точкой Q, то произведем исследование на чувствительность по прямым, пересекающихся в точке Q.
Сдвигая в сторону точки W, второй модели радиоприёмников будет уменьшаться, а количество радиоприёмников первой модели останется на том же уровне.
Рw = 60*30 + 0*20 = 1800 у.е.
Что на 500 у.е. меньше оптимального.
При дальнейшем исследовании модели на чувствительность начнём её перемещение по отрезку QR в сторону увеличения числа радиоприёмников второго типа и уменьшения числа первого.
Рe = 56*30 + 30*20 = 2280 у.е.
Что меньше оптимума на 20 у.е..
При дальнейшем продвижении по отрезку мы придём в точку R. В точку с максимально большим количеством радиоприёмников 1-й модели.
Рr = 20*30+75*20 = 2100 у.е.
Что на 100 у.е. меньше оптимального.
При устранении ограничения Х2=75, мы придём к точке E2 на прямой 0Х2, в которой прибыль будет равна Р = 100*20=2000, что на 300 у.е. меньше найденного оптимального в т.Q
При устранении ограничения Х1=60, мы придём к точке W2 на прямой 0Х1, в которой выпуск радиоприёмников второй модели равен нулю, а прибыль от производства будет:
Р = 80*30=2400, что на 100 у.е. больше оптимального в т.Q
Самое большое ограничение накладывается на максимальном запасе деталей:
Х1=60 и Х2=75.
Р=60*30+75*20=3300 у.е.
Т.е. при устранении мы приобретаем дополнительную прибыль – 1000 у.е.
На решение задачи имеют влияния ресурсы, а точнее их значение. Ресурсы можно разделить на дефицитные, которые при любом, даже незначительном уменьшении, влияют на решение задачи, и недефицитные, которые при уменьшении не влияют на решение задачи, пока они не переходят в категорию дефицитных (ОДР)
В данной задаче имеются 2 ресурса, охаратеризованные в уравнениях (1) и (2), оба они являются дефицитными, то есть их изменение приводит к перемещению точки оптимального решения.
1)Рассмотрим 2 ограничение:
Увеличим его количество до 65
Ценность
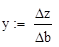

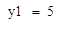
Следовательно, при изменении количества ресурса 2 на единицy прибыль растёт на 5 y.e.
2)Рассмотрим 1 ограничение:
Увеличим его количество до 850
Ценность
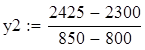

Следовательно, при изменении количества ресурса 1 на единицy прибыль растёт на 2.5 y.e.
Из этого делаем вывод, что ценность ресурса (2) в двое превышает ценность ресурса (1), следовательно максимизировать его будет значительно выгодней для получения лучших результатов.
3)Рассмотрим 3 ограничение:
Уменьшим его количество до 25(недифицитный)-точка оптимума
Ценность
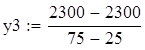
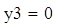
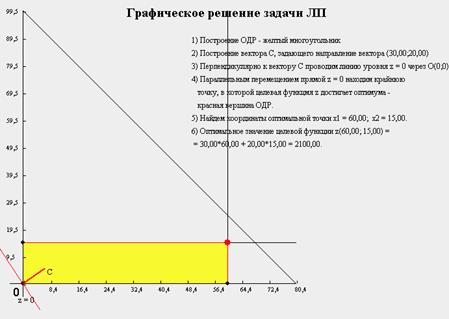
3)Рассмотрим 3 ограничение:
Уменьшим его количество до 15(недифицитный)-стал дефицитным
Ценность
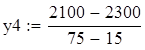

Благодаря исследованию чувствительности модели, мы получили информацию о ценности ресурса и оптимальном его использовании.