Теорема сложения вероятностей для совместных событий и ее модификации для случая трех и более событий.
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения.
Р(А+В) = Р(А) +Р(В) — Р(АВ)
Совместные события?
· Нет: Р(А+В) = Р(А) +Р(А)
· Да: Р(А+В)=Р(А)+Р(В) -Р(АВ)
Аналогично вероятность суммы трех событий вычисляется по формуле:
Р(А+В+С) = Р(А)+Р(В)+Р(С)- Р(АВ) — Р(АС) — Р(ВС)+Р(АВС)
Общая формула для вероятности сумы любого числа совместных событий:
5. Теорема умножения вероятностей для независимых событий и основные свойства независимых событий.
Р(АВ)=Р(А)*Р(В)
События А,В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие. Вероятности независимых событий называются безусловными.
Если события А и В независимы, то:
1) события А и В* независимы;
2) события А* и В независимы
3)события А* и В* независимы;
События А1, А2, Аn независимы в совокупности, если Р(А1,А2..Аn)= Р(а1)Р(А2)...Р(Аn)
События А1,А2..Аn попарно независимы, если в любой паре Аi; Аj события Ai и Aj независимы.
Независимость в совокупности и попарная независимость событий — понятия разные.
6. Теорема умножения вероятностей для зависимых событий, понятие условной вероятности и зависимости и независимости двух и более событий.
Вероятность произведений нескольких событий = произведению вероятностей одного из этих событий на условные вероятности других событий, вычисленные предположения, что все предшествующие события произошли для зависимых событий:
Р(А*В)=Р(А) *Р(В/А)
Условной вероятностью РА(В)=Р(В/А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Зависимость и независимость двух и более событий:
События называются зависимыми, если одно из них влияет на вероятность появления другого.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
Формула полной вероятности. Формула Байеса.
Вероятность события А, которое может наступить лишь при условии появления одного из событий В1, В2,..Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А.
Р(А) = Р(В1)* P(A/B1)+P(B2) +..+P(Bn)*P(A/Bn)
B1, В2..Вn — образуют полную группу событий.
Р(В1)+Р(В2)+..+Р(Вn)=1
любые события Bi и Вj попарно несовместны
Формула полной вероятности: P(A)=∑P(BiA)=∑P(Bi)*Pbi(A)
Событие А может произойти при условии появления одного из несовместных событий В1, В2,..Вn,, образующих полную группу. Пусть произведено испытание, в результате которого произошло событие А. Определим, как в связи с этим изменятся вероятности В1, В2,..Вn, т.е. Найдем условные вероятности Р(Вi/А)
Р(Вi/А)= Р(Вi)* Р(А/В1) / Р(В1)* Р(А/В1) + Р(В2)*Р(А/В2)+..Р(Вn)*P(A/Bn)= P(Bi)*P(A/Bi) / P(A)
Р(Вi) - априоные (доопытные) вероятности
Р(Вi/А) — апостериорные (послеопытные) вероятности
Отличие: формула вероятности употребляется, когда результат испытания неизвестен, событие А не наступило; а формула Байера применяется когда всё наоборот.
8. Повторные независимые испытания. Формула Бернулли.
Повторные независимые испытания - многократные испытания, в которых вероятность появления события А в каждом испытании не меняется в зависимости от исходов других испытаний
Под схемой Бернулли понимают проведение серий в n-испытаний, в каждом из которых 2 исхода. предполагается, что все n-испытания независимы и вероятность появления события А в каждом испытании постоянна и обозначается:
Пусть производится n независимых испытаний. Вероятность появления события А в каждом испытании одна и та же: -p; q=1-p
Формула Бернулли определяет вероятность появления события А в n независимых испытаниях ровно m раз. Pn(m)=Cmn*pm*qn-m= (n! / m!(n-m)!) * pm*qn-m
9. Повторные независимые испытания. Теорема Пуассона.
Если вероятность 
наступления события 
в каждом испытании постоянна и мала, а число независимых испытаний 
достаточно велико, то вероятность наступления события 
ровно 
раз приближенно равна
,
э. 
где λ ≤10
10. Повторные независимые испытания. Локальная теорема Муавра-Лапласа.
Локальная теорема Муавра- Лапласа. Если вероятность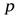 
наступления события 
в каждом испытании постоянна и удовлетворяет условиям 
, а число независимых испытаний 
достаточно велико, то вероятность 
может бить вычислена по следующей приближённой формуле
(12) 
, 
дает асимптотическую формулу (оно тем точнее, чем больше 
), позволяющую найти приближенное значение 
при достаточно больших значениях , гдефункция
(13) 
(Ф. Г.)
называется функцией Гаусса, а её график представляет кривой вероятностей.
11. Повторные независимые испытания. Интегральная теорема Муавра-Лапласа.
Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна
,
Где - 
функция (или интеграл вероятностей) Лапласа;
, 
.
Формула называется интегральной формулой МуавраЛапласа. Чем больше n, тем точнее эта формула. При выполнении условия npq ≥ 20 интегральная формула 
, так же как и локальная, дает, как правило, удовлетворительную для практики погрешность вычисления вероятностей.
Функция Ф(х) табулирована (см. табл.). Для применения этой таблицы нужно знать свойства функции:
1. Функция Ф(х) нечетная, Т.е. Ф(-х) = -Ф(х).
2. Функция Ф(х) монотонно возрастающая, причем при х → +∞ Ф(х) → 1 (практически можно считать, что уже при х > 4 Ф(х) ≈ 1).
.