Математическое ожидание случайных величин и его свойства

Мат. ожидание - это среднее значение случайной величины.

Свойства:

1) М (с) = с (с=const)

2) М (Х+У) = М (Х) + М(У)

3) М (Х-У) = М (Х) - М (У)

4) М (Х+-С) = М (Х) +- С

5) М (Х*У) = М (Х) * М(У) (Х и У независимы)

6) Х >= 0, то М(Х) >= 0

7) Х>=У, то М(Х)>=М(У)

Дисперсия случайной величины и ее свойства

Свойство 1. Дисперсия постоянной величины равна нулю

.

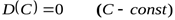Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат

.

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий

.

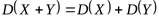Свойство 4. Дисперсия суммы независимых случайных величин равна сумме их дисперсий

. ●

Свойство 5. Дисперсия разности двух случайных независимых величин равна сумме дисперсий этих величин

.

Свойство 6. Дисперсия случайной величины равна математическому ожиданию

квадрата этой величины минус квадрат ее математического ожидания

.

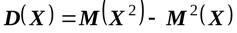Мода, медиана, квантили случайных величин

Модой непрерывной случайной величины называется точка локального максимума плотности распределения этой случайной величины

Модой дискретной случайной величины называется такое значение этой случайной величины, вероятность принятия которой больше, чем вероятности принятия соседних с ним значений

Медианой случайной величины X называется число x0, которое удовлетворяет условию:

Р (Х < Ме (Х)) = Р (Х > Ме (Х)) =

(5.20)

Квантилем уровня p называется число xp, которое удовлетворяет условию:

Биномиальный закон распределения и его основные характеристики

Биномиальный закон распределения (дискрет)

Биномиальным называют раcпределение вероятностей, определяемое формулой Бернулли

где 0<p<1, q=1-p, m=0, 1, 2,..., n.

Дискрет случайных величин имеет бинарный закон распределения, или она принимает целочисленные неотрицательные значения с вероятностями определенными по формуле Бернулли

Ряд распределения биномиального закона имеет вид:

xi				...	m	...	n
pi	qn			...		...	pn

Числовые характеристики биноминального распределения:

Теорема. Математическое ожидание случайной величины X, распределённой по биномиальному закону, M(X)=np, а её дисперсия D(X)=npq.

Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью p, равно p, т. е.

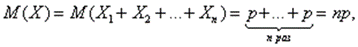
а её дисперсия:

Наивероятнейшее число наступлений события A в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, удовлетворяет неравенству np-q≤m0≤np+p.

Мода случайной величины, распределённой по биномиальному закону, - число целое - находится из того же неравенства np-q≤M₀(X)≤np+p.

Закон распределения Пуассона и его основные характеристики

Дискретная случайная величина Х имеет закон распределения Пуассона с параметром, если вероятности того, что она примет значения 0,1,2,...,m, соответственно равны:

, где m=0,1,2.

Построим ряд распределения:

				…	m	…
				…		…

Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, соответственно равны: M(X) = λ, D(X) = λ. Это характерная особенность распределения Пуассона.