Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
где параметр mx — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σx — среднеквадратическое отклонение (σx ² — дисперсия) распределения.
Нормальный закон распределения также называется законом Гаусса.
Найдём функцию распределения F(x).
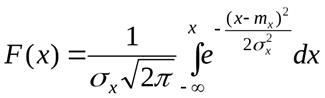
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Найдём экстремум функции.
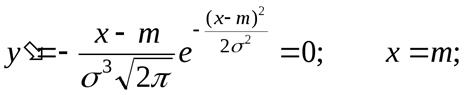
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m, то в точке х = т функция имеет максимум, равный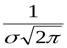 
.
5) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках значение функции равно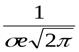 
.
Построим график функции плотности распределения.
Построены графики при т = 0 и трёх возможных значениях среднеквадратичного отклонения s = 1 и s = 2, s=7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.
Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.
При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой:
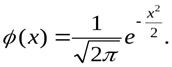
21.Равномерный закон распределения и его основные характеристики.
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a;b], если на этом отрезке ее плотность распределения вероятности постоянна, т. е. если дифференциальная функция f(х) имеет следующий вид:
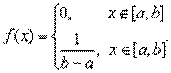
Тогда соответствующая функция распределения примет вид:
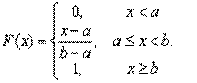
Графики функций f(x) и F(x) имеют вид:
Для равномерного закона распределения числовые характеристики могут быть вычислены по известным формулам:
Математическое ожидание: 
Дисперсия: 
Среднее квадратическое отклонение: 
Равномерно распределенная случайная величина X принимает все свои значения лишь в конечном промежутке [a;b], причем все эти значения случайной величины X равновероятны. Примерами случайных величин, распределенных по равномерному закону, могут быть:
· Время ожидания автобуса, при условии, что пассажир приходит на остановку в случайный момент времени и автобусы ходят с постоянным интервалом.
· Ошибки при взвешивании.
· Ошибка округления числа до целочисленного значения. Очевидно, что такая случайная величина распределена равномерно на отрезке [−0,5;0,5][−0,5;0,5].
22. Закон больших чисел. Неравенство Маркова. Неравенство Чебышева.
Закон больших чисел
ЗБЧ может пониматься в узком и широком смыслах
В широком – общий принцип, который, согласно Колмогорову, позволяет утверждать, что совокупность действий большого числа случайных факторов приводит к результату почти независимому от случая при некоторых общих условиях. Т.е при большом числе случайных величин их результат перестаёт быть случайным и может быть предсказан с высокой степенью определённости.
P (x>A) ≤ M(x) / A
В узком – группа теорем, устанавливающих факт приближения средних характеристик большого числа испытаний к некоторым постоянным.
Неравенство Чебышева
Для любых случайных величин имеющих D(x), M(x)
Неравенство Маркова
Если случайная величина X принимает только неотрицательное значение и имеет мат.ожидание, то для любого А>0 верно неравенство
(применимо к любым неотрицательным случайным величинам(верхняя граница оцениваемого события))