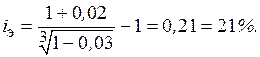Если условиями кредитного договора предусмотрено, что кредит и проценты по нему погашаются в течение его срока рядом платежей по указанной в договоре схеме, сумму процентов и общую погашаемую сумму можно определить, последовательно применяя приведенные ранее формулы. Рассмотрим типовые ситуации, связанные с таким погашением кредита.
а) Погашение основной суммы кредита равными частями.
При погашении кредита частями текущее значение суммы долга будет после очередной выплаты уменьшаться и, следовательно, будет уменьшаться сумма процентов, начисляемых на очередном интервале. Если сумма кредита равна D, срок кредита равен п лет и он погашается равными частями, выплачиваемыми в конце каждого года, то размер уплаты в конце первого года, включающей погашение части долга и выплату процентов за год, будет равен:

где g – годовая ставка процентов по кредиту в относительных единицах.
Остаток долга на начало второго года составит:

Размер уплаты в конце второго года будет равен:

Остаток долга на начало третьего года составит:

и т.д.
Сумма выплаченных процентов будет равна:

Применив к выражению в скобках формулу для суммы членов арифметической прогрессии, получаем:
 (2.1)
(2.1)
Общая сумма погашения кредита будет равна:

Если взносы в погашение кредита будут осуществляться р раз в году, сумма уплачиваемых процентов, определенная аналогичным образом, будет равна:
 (2.2)
(2.2)
При ежегодных уплатах формула (2.2) сводится к формуле (2.1).
Пример …
Кредит в размере 5 млн. руб., выданный по ставке 80% годовых, должен погашаться равными суммами в течение 5 лет. Определить размеры ежегодных уплат (план погашения долга) и сумму выплаченных процентов, если погасительные платежи осуществляются: а) один раз в конце года; б) по полугодиям.
Решение
а) Сумма уплаты в конце первого года будет равна:
 руб.
руб.
Остаток задолженности на начало второго года составит:
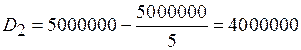 руб.
руб.
Для последующих лет получаем (в млн. руб.):
S 2 = 4,2; D 3 =3,0; S 3 = 3,4; D 4 = 2,0;
S 4 = 2,6; D 5 = l,0; S 5 = l,8; D 6 = 0.
Общие расходы по погашению кредита составят:
S = 5 + 4,2 + 3,4 + 2,6 + 1,8 = 17 млн. руб.
Сумма выплаченных процентов будет равна:
I = 17 – 5 = 12 млн. руб.
Если использовать формулу (2.1), получаем тот же результат:
 руб.
руб.
б) Сумма уплаты по кредиту в конце первого полугодия составит:
 руб.
руб.
Остаток задолженности по кредиту на начало второго полугодия будет равен:
D 2 = 5 000 000 – 500 000 = 4 500 000 руб.
Для последующих моментов выплат по кредиту получаем (в млн. руб.):
S 2 = 2,3; D 3 = 4,0; S 3 = 2,1; D 4 = 3,5; S 4 = 1,9; D 5 = 3,0;
S 5 = 1,7; D 6 = 1,5; S 6 = 1,5; D 7 = 2,0; S 7 = 1,3; D 8 = 1,5;
S 8 = 1,1; D 9 = 1,0; S 9 = 0,9; D 10 = 0,5; S 10 = 0,7; D 11 = 0.
Общие расходы по погашению кредита будут равны:
S = 2,5 + 2,3 + 2,1 + 1,9 + 1,7 + 1,5 + 1,3 + 1,1 + 0,9 + 0,7 = = 16 млн. руб.
Сумма выплаченных процентов составит:
I = 16 – 5 = 11 млн. руб.
Тот же результат может быть получен по формуле (2.2):
 руб.
руб.
б) Погашение кредита равными срочными уплатами.
Кредиты могут погашаться равными срочными уплатами, включающими погашение основной суммы долга и выплату соответствующей суммы процентов. Если проценты за кредит начисляются по простой ставке, общая их сумма I будет определяться приведенной выше формулой (2.2).
Общая сумма расходов по погашению кредита в размере D будет равна:
S = D + I.
и, следовательно, размер одинаковых срочных уплат будет равен:
 (2.3)
(2.3)
где п – срок кредита в годах; р – количество уплат в году.
В литературе для случая погашения индивидуальных ссуд, возмещаемых ежемесячными фиксированными взносами, можно встретить следующие формулы:
Стоимость кредита =
= 
Ежемесячный взнос =
= 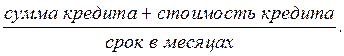
Как легко видеть, эти формулы являются частным случаем формул (2.2) и (2.3) для р = 12.
Начисление процентов по таким формулам называется также «методом 78». Это связано с тем, что для кредита сроком 12 месяцев ежемесячный размер погашения будет равен 1/12 его суммы. Следовательно, проценты за 1-й месяц будут начисляться со всей (12/12) суммы кредита, за 2-й – с 11/12 суммы кредита, за 3-й – с 10/12 суммы кредита и так далее до последнего месяца, проценты за кредит в котором будут браться с 1/12 суммы кредита. Сумма числителей таких дробей будет равна:
12+11 + 10+ 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2+1 = 78,
что и дало название подобному методу начисления процентов.
Пример …
Потребительский кредит на сумму 600 тыс. руб. открыт на 2 года по ставке 40% годовых. Погашение кредита должно осуществляться равными взносами. Определить стоимость кредита, погашаемую сумму и размер взносов, если погашение кредита будет осуществляться: а) ежеквартально; б) ежемесячно.
Решение
а) При ежеквартальных взносах стоимость кредита (сумма процентов за кредит) по формуле (2.2) будет равна:
 руб.
руб.
Погашаемая сумма составит:
S = 600 000 + 270 000 = 870 000 руб.
Размер ежеквартальных взносов будет равен:
 руб.
руб.
б) При ежемесячных выплатах стоимость кредита составит:
 руб.
руб.
Погашаемая сумма будет равна:
S = 600 000 + 250 000 = 850 000 руб.
Размер ежемесячного взноса составит.
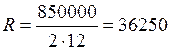 руб.
руб.
При погашении равными срочными уплатами долгосрочных кредитов с начислением процентов по сложной ставке размеры срочных уплат могут быть определены, если пересчитать (привести) суммы уплат к моменту выдачи кредита, или, иначе говоря, осуществить их дисконтирование с использованием формулы (1.19).
Если платежи размером R будут осуществляться ежегодно в конце каждого года, то их значения, дисконтированные по сложной ставке процентов i на начало первого года выплат, будут равны:

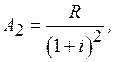

Применив к сумме этих величин формулу для суммы членов геометрической прогрессии, получаем для современной (приведенной) величины суммы всех платежей следующее выражение:
 (2.4)
(2.4)
Из этой формулы можно определить размер платежа:
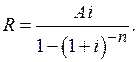 (2.5)
(2.5)
Поскольку сумма всех платежей по погашению кредита и начисленных процентов должна быть равна сумме кредита D, размер уплат, вносимых в конце каждого года при ставке сложных процентов i, по формуле (2.5) будет равен:

Общая сумма погашения кредита составит:

а сумма выплаченных процентов будет равна:
I = S – D.
Если равные выплаты по кредиту в размере R будут вноситься р раз в году, их размер, определенный аналогичным образом, составит:
 (2.6)
(2.6)
Пример …
Кредит в сумме 10 млн. руб. с ежегодным начислением сложных 46 процентов по ставке 20% годовых должен погашаться в течение 5 лет равными срочными уплатами. Определить размер срочной уплаты, общие расходы заемщика по погашению кредита и сумму выплаченных процентов, если выплаты по кредиту будут осуществляться: а) в конце каждого года; б) в конце каждого полугодия.
Решение
а) При выплатах по кредиту в конце каждого года сумма срочной уплаты по формуле (2.5) будет равна:
 руб.
руб.
Общие расходы заемщика по погашению кредита составят:
S = 5 × 3 343 797 = 16 718 985 руб.
Сумма выплаченных процентов будет равна:
I = 16 718 985 – 10 000 000 = 6 718 985 руб.
б) При выплатах по кредиту в конце каждого полугодия сумма срочной уплаты по формуле (2.6) будет равна:
 руб.
руб.
Общие расходы по кредиту составят:
S = 10 × 1 595 745 = 15 957 450 руб.
Сумма выплаченных процентов будет равна:
I = 15 957 450 – 10 000 000 = 5 957 450 руб.