Планетарными называют передачи, имеющими зубчатые колёса с подвижными осями вращения. Одноступенчатая конструкция ПЗП представлена на рис.8. Она состоит из центральных колёс 1,3, водила-Н и сателлитов 2. Сателлиты 2 находятся в зацеплении с колёсами 1,3 и подвижно соединены вращательной парой О2 с водилом Н.
Ведущее колесо 1 вращается на валу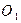 
, а колесо 3 неподвижно. При вращении колеса 1 с угловой скоростью
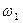движение от него передаётся сателлитам 2, которые перекатываются по неподвижному колесу 3 с угловой скоростью 
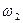, вокруг мгновенного центра вращения Р. Кроме того, сателлиты вращают водило Н со скоростью 
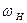вокруг оси ОН, которая является ведомой. Данная передача называется редуктором Джемса.
Для устранения силового и динамического дисбаланса угол между сателлитами равен строго 
. Угловое положение сателлитов 2 фиксируется осями водила Н.
Для определения передаточного отношения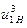 
от колеса 1 к водилу Н при неподвижном колесе 3 применяют метод Виллиса. Его основная идея состоит в том, что водило Н считают неподвижным, а у остальных элементов передачи угловые скорости уменьшаются на 
.
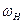Передаточное отношение механизма равно
,
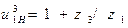где z1 и z3 – число зубьев колёс 1 и 3. Рекомендуемое значение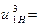 
4...8.
Угловые скорости водила Н и сателлита 2 составляют:
.
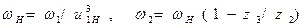КПД передачи определяется соотношением
,
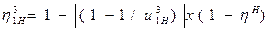где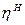 
- КПД за счёт потерь энергии в зацеплениях и опорах.
Усилие, передаваемое с центрального колеса 1 распределяется равномерно между сателлитами на nW зацеплений. Исходя из уравнения равновесия и учитывая, что силы направлены по линии зацепления можем записать
,
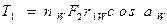где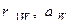 
- радиус начальной окружности колеса 1 и угол зацепления; nW – число сателлитов.
Отсюда,
.
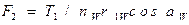В реальных передачах из-за технологических погрешностей изготовления зубчатых колёс вращающий момент распределяется неравномерно между сателлитами, что учитывается коэффициентом неравномерности Кн. При наличие механизма выравнивания нагрузок Кн=1,1-1,2.
Таким образом, передача усилия по нескольким направлениям снижает рабочую нагрузку в ПЗП, что даёт возможность снизить её массу и габариты.
Распространены различные конструкции одноступенчатых передач с большими передаточными отношениями, но при низком КПД. Применяются и многоступенчатые планетарные редукторы. ПЗП с двумя и более степенями свободы называются дифференциальными.
Для расчёта ПЗП необходимо выполнение ряда необходимых условий: соосности, соседства и сборки.
Условие соосности соблюдается при равенстве межосевых расстояний для двух пар колёс, то есть
z3-z1=2z2.
По условию соседства в ПЗП не допускается касания зубьев их вершинами, что сводится к неравенству
.
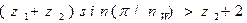По условию собираемости оси сателлитов должны находиться при сборке на равных угловых расстояниях друг от друга. В этом случае оси симметрии впадин центральных колёс должны совпадать с осями симметрии противоположных зубьев сателлитов. При повороте колеса 1 на угловой шаг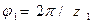 
ось сателлита повернётся на угол 
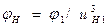. Поэтому теоретическое число сателлитов равно
.
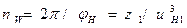Т.к.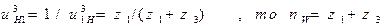 
.
Реально число сателлитов будет меньше в cW раз, т.е.
,
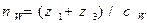где сW – целое число.
Расчёты ПЗП на прочность проводят для обращённого механизма по уравнениям для передач с геометрически неподвижными осями вращения.
Лекция 9.
ВОЛНОВЫЕ ПЕРЕДАЧИ.
Их основные преимущества: малая масса и габариты, большие передаточные числа u=80-300, малые нагрузки на валы, высокая кинематическая точность.
Конструкция ВЗП показана на рис.9. Она состоит из генератора волн h, гибкого g и жёсткого b колёс. Зубчатый венец гибкого колеса деформируется генератором волн и входит в зацепление с жёстким колесом в зонах у точек А и G. Гибкое колесо выполнено в виде стакана, на внешней поверхности которого в средине нарезан зубчатый венец. Генератор состоит из вала и профилированного кулачка с закреплённым на нём гибким подшипником.
При принудительном задании деформации гибкому колесу её форма определяется профилем кулачка или диска, при свободном – одной или двумя парами роликов.
Кинематика и геометрия ВЗП. Обычно используются передачи с 1 степенью свободы с неподвижным гибким или жёстким колесом. В первом случае вращение жёсткого колеса и вала генератора совпадает, а при остановленном жёстком колесе вращение противоположное. Рассмотрим 2-х волновой генератор при заданном передаточном отношении.
Число зубьев жёсткого zb и гибкого zg колёс:
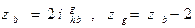
(при остановленном жёстком колесе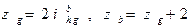 
).
Диаметр делительной окружности гибкого колеса
,
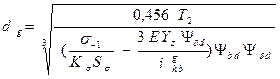где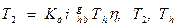 
-вращающие моменты на выходном валу и генераторе волн; η-КПД передачи; σ-1 - предел выносливости материала колеса; К 
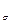=1,8-2 - коэффициент концентрации напряжений у корня зуба; Sσ=1,3-1,7 -запас прочности; Yz=1,35-1,5 - коэффициент влияния зубчатого венца на прочность гибкого колеса;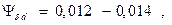 
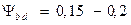-коэффициенты относительной толщины и ширины зубчатого венца. При неподвижном жёстком колесе 
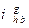меняется на 
.
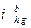Расчётный модуль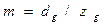 
уточняют до ближайшего большего стандартного значения. Далее вычисляют геометрические параметры колеса (см. рис.10).
Радиальное смещение при деформации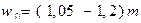 
;
коэффициент смещения хg=3-4; высота зубьев и глубина захода hg=(1,5-1,8)m, hd=(1,3-1,5)m; толщина стенки гибкого колеса h1=(0,005-0,015)dg.
Затем вычисляют коэффициент смещения жёсткого
колеса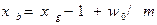 
;
диаметры окружностей впадин и вершины гибкого колеса
;
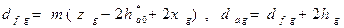диаметры окружностей впадин и вершины жёсткого колеса
,
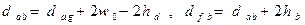где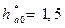 
при m<0,5 и 
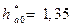при m>0,5 – коэффициент высоты головки долбяка. Приближённо принимают hb=hg.
Гибкие колёса при работе волновой передачи подвергаются циклическому нагружению от генератора волн. Уровень напряжений в их тонкостенной оболочке достаточно высок, особенно на зубчатом венце, где имеется концентрация напряжений. Основной причиной выходя из строя ВЗП является усталостное разрушение.
Поэтому проводится расчёт гибкого колеса на прочность, который включает в себя:
- определение напряжений от изгиба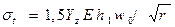 
,
напряжений растяжения от окружных сил в зацеплении
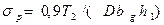и касательных напряжений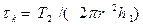 
от нагружения крутящим моментом, где D-внутренний диаметр стакана, h1-толщина стенки от впадины зуба,
r - радиус срединной поверхности оболочки;
- оценку прочности по условию
,
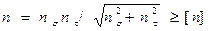где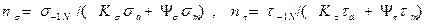 
;
;
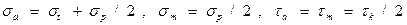n,[n]-расчётный и допускаемый коэффициенты запаса прочности;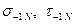 
-пределы ограниченной выносливости для нормальных и касательных напряжений; Kσ,Kτ-эффективные коэффициенты концентрации.
Принимают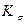 
=1,8-2, K 
=(0,7-0,8)Kσ,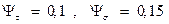 
.