Их назначение передавать вращение под углом, чаще всего с углом пересечения осей 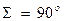 . В ЛА получили распространение КЗП с прямыми и круговыми зубьями; последние имеют в 1,5 раза большую несущую способность при тех же габаритах. КЗП выполняют с различными осевыми формами зубьев. Рассмотрим пропорционально понижающиеся зубья, где вершины делительного конуса и конуса впадин сходятся в одной точке. Геометрические параметры подобной передачи с прямыми зубьями показаны на рис.7.
. В ЛА получили распространение КЗП с прямыми и круговыми зубьями; последние имеют в 1,5 раза большую несущую способность при тех же габаритах. КЗП выполняют с различными осевыми формами зубьев. Рассмотрим пропорционально понижающиеся зубья, где вершины делительного конуса и конуса впадин сходятся в одной точке. Геометрические параметры подобной передачи с прямыми зубьями показаны на рис.7.
Кинематика и геометрия.
Делительные диаметры в торцевом и среднем сечении определяют из равенств
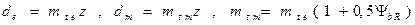 ,
,
где z – число зубьев; mtm, mre – средний и внешний торцевые модули; 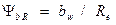 =0,25...0,35 – относительная ширина зубчатого венца.
=0,25...0,35 – относительная ширина зубчатого венца.
Для колёс с прямым зубом стандартизован внешний торцевой модуль mte. Величины внешнего Re и среднего Rm конусных расстояний находят по формулам
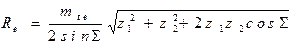 ,
, 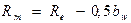 . (а)
. (а)
Внешний диаметр вершин зубьев в торцевом сечении
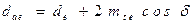 ,
,
где δ – угол делительного конуса колеса.
Высота головки hae и ножки hfe прямого зуба hae=mte, hfe=1,2mte.
Передаточное число конической передачи
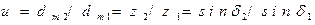 .
.
При 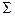 =90о u=tgδ2=ctgδ1. Этим соотношением и пользуются при заданном u для вычисления углов δj.
=90о u=tgδ2=ctgδ1. Этим соотношением и пользуются при заданном u для вычисления углов δj.
Углы головки и ножки зуба находят по формулам:
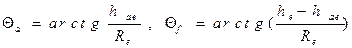 .
.
Отсюда, углы конуса вершин и впадин равны:
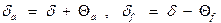 .
.
В отличие от ЦЗП область высотного корригирования для КЗП расширена. Поэтому внешний диаметр и высоту головки зуба определяют так:
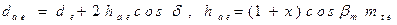 .
.
Профиль зубьев конических колёс близок к эвольвентному профилю цилиндрического прямозубого колеса. Диаметр начальной окружности и число зубьев эквивалентного колеса равны:
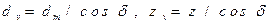 .
.
Передаточное отношение эквивалентной передачи
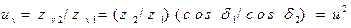 .
.
Расчёт на прочность КЗП.
На рис.8 показано распределение сил на контакте в КЗП. В зацеплении прямозубой передачи действуют Ft–
окружная, Fr–радиальная и Fa–осевая силы. Раскладывая нормальную силу Fn на Ft и Fr*, а Fr*- на Fa и Fr, имеем:
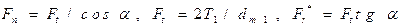 , или
, или
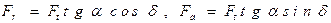 .
.
Направление сил на другом колесе – противоположное.
Особенность расчёта на прочность конических колёс состоит в том, что их основные параметры определяются для эквивалентного прямозубого цилиндрического колеса. При вычислении контактных напряжений в зубе шириной bw=
=b1=b2 удельная расчётная окружная сила равна
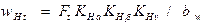 .
.
При определении коэффициента динамичности 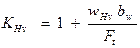 в удельной окружной динамической силе значения δH, g0 и wv находят также как для ЦЗП.
в удельной окружной динамической силе значения δH, g0 и wv находят также как для ЦЗП.
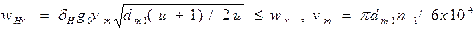 .
.
Контактные напряжения рассчитывают по формуле
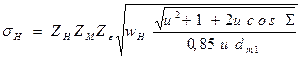 ,
,
где ZH=2,5cosβm (при 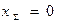 ).
).
Условие контактной прочности 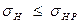 . При перегрузке не более 10...15% можно увеличить ширину венца bw, но в сторону внутреннего торца; при этом Re не изменится. В противном случае надо перейти на ближайший больший стандартный модуль и повторить расчёты.
. При перегрузке не более 10...15% можно увеличить ширину венца bw, но в сторону внутреннего торца; при этом Re не изменится. В противном случае надо перейти на ближайший больший стандартный модуль и повторить расчёты.
Конусное расстояние Re вычисляют по формуле
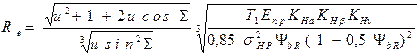 .
.
Из равенства (а) находим торцевой внешний модуль
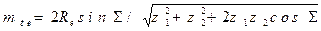
и округляем его до ближайшего стандартного значения.
Далее определяем основные геометрические характеристики
При вычислении напряжений изгиба удельная окружная сила равна
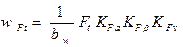 .
.
Окружная динамическая сила при учёте динамики нагружения
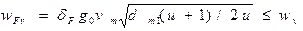 , δF=0,016.
, δF=0,016.
Напряжения изгиба вычисляют аналогично как для цилиндрического колеса по среднему торцевому модулю.
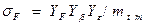 .
.
Условие прочности зубьев конической шестерни или колеса на изгиб
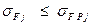 .
.
Лекция 8.
ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ.