Блок векторизован и реализует математическую модель звена, динамика которого описывается линейным уравнением с запаздыванием вида:
y (t) = x (t - T),
где x(t) – вектор входных сигналов в блок; y(t) – вектор выходных сигналов из блока; Т - вектор времен запаздывания.
При нулевых начальных условиях динамика блока может быть представлена следующей передаточной функцией (для скалярного варианта сигналов):
W(s) = e - t × S ,
поэтому пиктограмма данного блока имеет вид передаточной функции идеального запаздывающего звена.
Обязательное условие: t > 0.
Диалоговое окно блока имеет 2 диалоговые строки.
Для работы блока необходимо задать:
В 1-ой диалоговой строке - вектор времен запаздывания T ( в секундах);
Во 2-ой диалоговой строке – начальный размер стека.
Примеры заполнения 1-ой строки диалогового окна:
Скалярный вход
Диалоговая строка - 2.3
Векторный вход (3 одинаковых звена)
Диалоговая строка - 3#2.3
Векторный вход (3 разных звена)
Диалоговая строка - 2.3 1.8 3.3 (через пробел)
Примечания:
1. По умолчанию данный блок реализует преобразование скалярного входного сигнала.
2. По умолчанию в данном блоке начальный размер стека – 1000.
Квадратичный функционал качества
Блок векторизован и реализует интегральное преобразование:
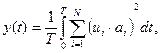(квадратичный функционал качества),
где T = t - текущее модельное время; ui(t) - мгновенное значение вектора входного сигнала; ai – вектор весовых коэффициентов; у(t) - выходной сигнал.
Диалоговое окно блока имеет 1 диалоговую строку.
Для работы блока в диалоговой строке необходимо задать вектор весовых коэффициентов.
Примеры заполнения диалогового окна:
Скалярный вход
Диалоговая строка - 2
Векторный вход (3 одинаковых весовых коэффициента)
Диалоговая строка - 3#2
Векторный вход (3 разных весовых коэффициента)
Диалоговая строка - 2.3 1.8 3.3 (через пробел)
Примечание. По умолчанию данный блок реализует преобразование скалярного входного сигнала.
Новый” блок
Учитывая, что невозможно сформировать абсолютно полную библиотеку типовых блоков, в ПК “МВТУ” разработаны средства, которые позволяют Пользователю расширить состав личной библиотеки за счет создания новых типов блоков, например, посредством встроенного Интерпретатора математических функций, на базе которого функционирует и “ Новый” блок, позволяющий прямо в процессе работы создавать экземпляры блоков со своими оригинальными математическими моделями.
Диалоговое окно этого блока - фактически окно текстового редактора, в котором Пользователь записывает математическую модель в виде, близком к естественной записи.
Математическое описание блока соответствует многомерной нелинейной динамической системе в форме Коши:
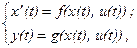
где f(x, u), g(x, u) - известные нелинейные функции переменных состояния (x1, x2,...xn) и входных воздействий (u1, u2,...um), причем в качестве входных воздействий могут выступать и коэффициенты (как постоянные, так и переменные), входящие в любое из уравнений системы.
Первое из уравнений системы может отсутствовать; в этом случае “ Новый” блок выполняет алгебраические преобразования входных величин.
Использование «Нового» блока в качестве функционального весьма эффективно в случае наличия в модели сложных функциональных преобразований, когда использование для этих целей элементарных функциональных типовых блоков приведет к неоправданному усложнению структурной схемы.
В таблице 1.7 приведен перечень математические операции и функции, которые «Новый» блок интерпретирует («распознает»):
Таблица 1.7 – Интерпретируемые математические операции и функции
| +сложение | abs - модуль | sin- синус | arcsin- арксинус |
| -вычитание | sign - знак | cos - косинус | arccos - арккосинус |
| *умножение | exp - экспонента | tg - тангенс | arctg- арктангенс |
| /деление | ln– логарифм натуральный | ctg- котангенс | arcctg - арккотангенс |
| ^ степень | log – логарифм десятичный | pi - 3.1415..... | () - cкобки |
Дополнительно «Новый» блок “распознает” ряд специальных функций:
time - модельное время;
step – смещенное ступенчатое воздействие;
sqrt - корень квадратный;
if - вычисление по условию;
for - формирование векторных данных посредством циклических операций;
interpol – интерполяция данных (линейная, степенная).
Например, запись u = step(t_вкл, y_нач, y_кон); означает, что через время t_вкл после начала моделирования переменная u изменит (скачком) свое значение с y_нач на y_кон. Параметры функции step могут быть заданы как в числовом виде, так и через именованные параметры, значения которых должны быть определены выше по тексту в этом же окне или окне Редактора Глобальных параметров …
Запись pp = if(bb, a1, a2, a3) означает, что переменная pp принимает значения:
pp = a1, если именованная переменная bb < 0;
pp = a2, если именованная переменная bb = 0;
pp = a3, если именованная переменная bb > 0.
В Интерпретатор математических функций и, соответственно, в «Новый» блок настоящей версии ПК «МВТУ» включено 8 новых специальных функций, реализующих определение основных термодинамических свойств воды и водяного пара (известные таблицы Вуколовича в докритическом диапазоне: давления от 0.09 до 20 МПа и температуры от 10 до 360 градусов Цельсия).
Запись этих функций имеет вид:
waterps(P,flag); - вычисление свойств воды по давлению на линии насыщения;
waterts(T,flag); - вычисление свойств воды по температуре на линии насыщения;
steamps(P,flag); - вычисление свойств пара по давлению на линии насыщения;
steamts(Т,flag); - вычисление свойств пара по температуре на линии насыщения;
waterpt(P,T,flag); - вычисление свойств воды по давлению и температуре;
waterph(Р,H,flag); - вычисление свойств воды по давлению и энтальпии;
steampt(P,T,flag); - вычисление свойств пара по давлению и температуре;
steamph(P,H,flag); - вычисление свойств пара по давлению и энтальпии.
Например, запись v_уд= waterps(1е6,4); соответствует вычислению удельного объема воды v_уд (flag равен 4) на линии насыщения при давлении 1.0е6 Па (1 МПа).
Значения параметра flag могут изменяться от 1 до 8 и соответствовать вычислению следующих термодинамических характеристик воды или водяного пара:
1 – давление; 2 – температура; 3 – энтальпия; 4 – удельный объем; 5 – число Прандтля;
6 – динамическая вязкость; 7 – коэффициент теплопроводности; 8 – энтропия.
Входные параметры и возвращаемые значения термодинамических параметров воды или водяного пара представляются в системе СИ (за исключением температуры, которая измеряется в градусах Цельсия).
Процедуры формирования математической модели динамики какого-то устройства или фрагмента рабочего процесса с использованием «Нового» блока рассмотрим на примере формирования уравнений динамики Объекта Управления САР (см. рисунок 1.22).
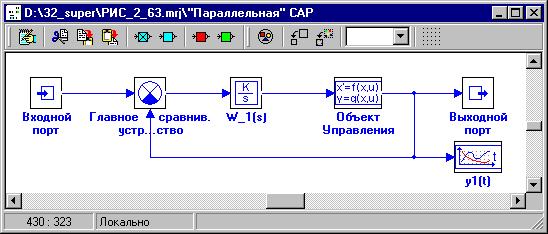
Рисунок 1.22
Математическое описание динамики Объекта Управления приведено к системе ОДУ в форме Коши:
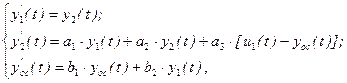
где начальные условия для всех динамических переменных y1, y2 и y_oc - нулевые.
На рисунке 1.23 (ниже по тексту) представлена экранная копия окна Редактор интерпретатора математических функций с введенной математической моделью динамики Объекта Управления и комментариями к ней...
Если «Новый» блок имеет входы (входные порты), то первая исполняемая строка (не считая строку комментария) обязательно должна содержать оператор input, описывающий входные сигналы в данный блок, включая имя входа и его размерность.
В данном примере 1-я исполняемая строка (input u1;) присваивает 1-му (и единственному) входу уникальное имя – u1.
Если бы, например, этот блок имел бы 2 входа, причем 1-ый вход – «трехжильный» (векторный), а 2-ой – «пятижильный», то 1-я исполняемая строка имела бы вид:
input u1[3], g[5];
Для описания размерности входов используются прямоугольные скобки.
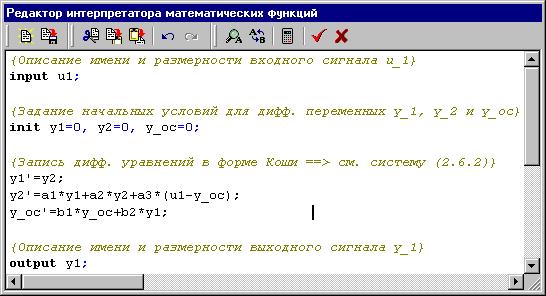
Рисунок 1.23
Если «Новый» блок описывает динамику объекта моделирования в виде системы дифференциальных уравнений в форме Коши, то вторая исполняемая строка (не считая строку комментария) обязательно должна содержать оператор init, описывающий начальныеусловия для динамических (дифференциальных) переменных, ниже по тексту для которых будут записаны обыкновенные дифференциальные уравнения в форме Коши.
В данном примере 2-я исполняемая строка
init y1=0, y2=0, y_oc=0;
задает начальные условия (при t = 0) для трех динамических переменных: y1, y2 и y_oc.
В том случае, когда математическая модель динамики блока описывается большим числом дифференциальных уравнений, например, 5-ю, то 2-я исполняемая строка будет иметь вид:
init x1=0, x2=1, x3=2, z=0, R=0;
где х1, х2, х3, z, R – динамические переменные, для которых ниже по тексту будут записаны дифференциальные уравнения (точнее система уравнений) в форме Коши.
Непосредственно дифференциальные уравнения динамики Объекта Управления записаны с 3-ей по 5-ую исполняемые строки, где символ апострофа обозначает производную по времени, а значения коэффициентов a1, a2, a3, b1, b2 передаются в “Новый” блок через механизм Глобальных параметров (см. соответствующий подраздел в «Инструкции Пользователя»).
Если «Новый» блок имеет выходы (выходные порты), то последняя исполняемая строка обязательно должна содержать оператор output, описывающий выходные сигналы из «Нового» блока, включая имена выходов и их размерности.
В данном примере последняя строка (output y1;) описывает один выходной сигнал (y1) без указания в прямоугольных скобках размерности выходного сигнала.
Если бы «Новый» блок имел 2 векторных выхода (2-х жильный и 3-х жильный), то последняя исполняемая строка имела бы, например, вид:
output z1[2], z2[3];
В этом случае выше по тексту необходимо было определить (рассчитать) все составляющие выходных сигналов, например:
z1[1]=a1+sin(y1); z1[2]=exp(y2); z2[1]=y1*y2; z2[2]=sqrt(abs(y_oc)); z2[3]=(y2)^a2;
После ввода всего текста в окно Редактор интерпретатора математических функций переместите курсор на командную кнопку Применить (2-я справа) и сделайте щелчок левой клавишей «мыши»: окно Редактор интерпретатора математических функций закроется и станет активным Схемное окно, в котором «Новый» блок будет иметь один входной и один выходной порты (см. рисунок 1.22 выше по тексту).
Если бы «Новый» блок формировал два выхода (например, z1 и z2 ==> см. выше), то изображение «Нового» блока на структурной схеме имело бы два выходных порта. При ориентации блока «слева-направо» первый выходной порт будет верхним, а второй выходной порт – нижним.
Для создания математической модели рабочего процесса, описываемого сложными нелинейными дифференциальными уравнениями с переменными коэффициентами (например, процессы теплогидравлики в элементах теплофизического оборудования), целесообразнее использовать «Новый» блок только для формирования правых частей системы дифференциальных уравнений (записанных в форме Коши).
В таком варианте процедуру интегрирования можно реализовать с использованием типового блока Интегратор (блок векторизован), расположенного за «Новым» блоком, причем выходной сигнал блока Интегратор (обычно векторный) подается на вход «Нового» блока, не образуя алгебраической «петли» (контура).
Реализуем такой подход для формирования математической модели блока Объект Управления в САР (см. рисунок 1.24 ниже по тексту).
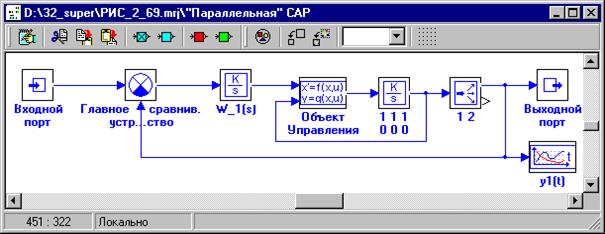
Рисунок 1.24
В верхней части рисунка 1.25 представлена экранная копия окна Редактор интерпретатора математических функций, в котором реализован алгоритм вычисления правых частей дифференциальных уравнений, описывающих динамику блока Объект Управления.
Только внешне основной текст (по сравнению с рисунком 1.23) изменился незначительно. Кардинальным образом изменился «смысл» символа апостроф: теперь запись y1’=… обозначает не первое дифференциальное уравнение, а просто определяет новую переменную с именем y1’. Появился новый входной сигнал y, который является «трехжильным» (векторным) и вводит в «Новый» блок значения динамических переменных y1, y2 и y_oc после каждого шага интегрирования (в том числе и пробного шага). На выход «Нового» блока сформирован векторный сигнал y_out с размерностью, равной трем ==> y_out = [y1 y2 y_oc].
Подпись (в две строки) под типовым блоком Интегратор (см. рис. 3 выше по тексту) «сообщает», что данный блок выполняет операцию интегрирования в «векторном» варианте, причем в его диалоговом окне установлены коэффициенты усиления 1 1 1 (три числа 1 через пробел) и нулевые начальные условия (три числа 0 через пробел). Блок Демультиплексор «извлекает» из вектора сигнал y1.
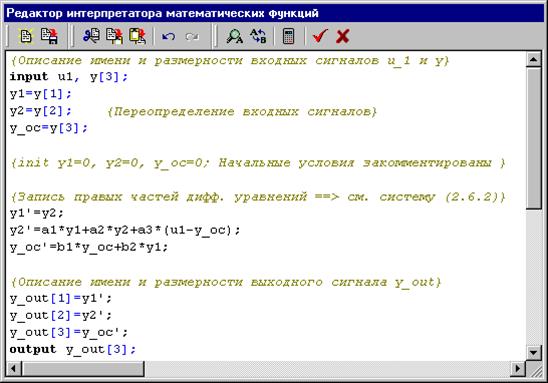
Рисунок 1.25
Более подробную информацию о примерах использовании «Нового » блока для формирования «оригинальных» математических моделей динамики можно найти в соответствующем разделе «Инструкции Пользователя» ПК «МВТУ», а также во многих демонстрационных примерах, расположенных в подкаталоге …/DEMO.