Комплексный коэффициент передачи по напряжению определяется выражением
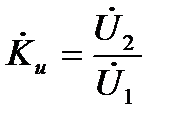, (3.1)
аналогично вводятся в рассмотрение комплексный коэффициент передачи тока
(3.2)
и коэффициент (не комплексный) передачи мощности
, (3.3)
где 
- мощность, потребляемая четырехполюсником;
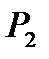- мощность, передаваемая в нагрузку.
Для расчета коэффициентов передачи необходимо при заданном источнике входного сигнала определить комплексные амплитуды входного и выходного напряжений, токов или мощностей.
Рис. 3.1
В качестве примера рассмотрим четырехполюсник, схема которого показана на рис.3.1, и определим его комплексный коэффициент передачи напряжения вида (3.1).
Рис. 3.2
Подключим на вход четырехполюсника идеальный источник напряжения с ЭДС 
, как показано на рис.3.2, и воспользуемся методом узловых напряжений. В цепи имеется два узла и необходимо определить единственное узловое напряжение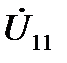 
.
Выражая через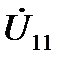 
токи ветвей, и используя первый закон Кирхгофа, получим уравнение метода узловых напряжений:
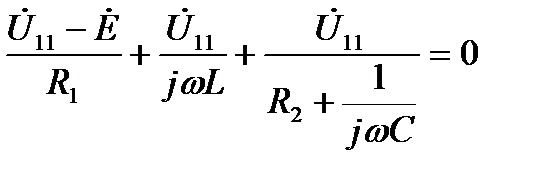
После алгебраических преобразований получим
.
Тогда по Закону Ома можно определить выходное напряжение
.
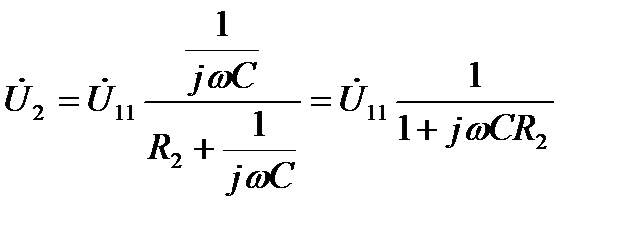Подставляя выражение для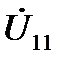 
, с учетом 
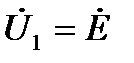получим
.
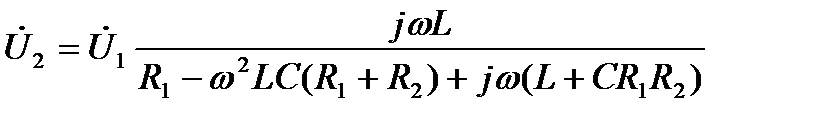Комплексный коэффициент передачи четырехполюсника по напряжению равен
.
Как видно,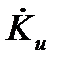 
- комплексная функция частоты сигнала, ее называют комплексной частотной характеристикой (КЧХ). Графически она отображается линией в трехмерном пространстве (ось 
и две оси для отображения комплексного числа), что неудобно практически.
На плоскости КЧХ изображается в виде годографа. Для его построения заданный интервал частот разбивается с равномерным шагом, для каждого значения частоты вычисляются и отображаются на комплексной плоскости по осям абсцисс и ординат соответственно действительная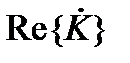 
и мнимая 
составляющие комплексного коэффициента передачи.
Пример годографаКЧХ цепи пр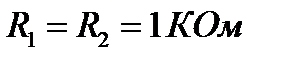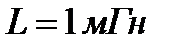и 
, 
и 
показан на рис.3.3.
Рис. 3.3
Стрелка показывает направление увеличения частоты входного сигнала.
На частоте
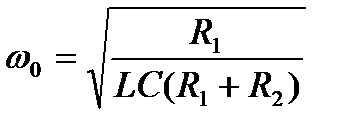
величина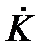 
действительна, а точка годографа расположена на оси абсцисс.
Амплитудно-частотная и фазочастотная характеристики
Четырехполюсника
Комплексный коэффициент передачи четырехполюсника можно представить в показательной форме
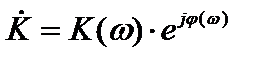, (4.1)
где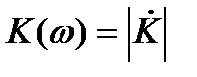 
- его модуль;
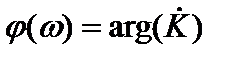- аргумент.
Амплитудно-частотная характеристика (АЧХ)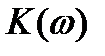 
представляет собой зависимость модуля комплексного коэффициента передачи от частоты. Она представляет собой отношение амплитуд или действующих значений выходного сигнала к входному.
Фазочастотная характеристика (ФЧХ)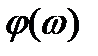 
– это зависимость от частоты аргумента комплексного коэффициента передачи. Она представляет собой сдвиг фаз между выходным и входным сигналами.
Обычно выражение для 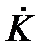представляет собой дробь с комплексными числителем и знаменателем, которую необходимо представить в виде
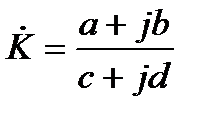. (4.2)
Тогда модуль частного (дроби) равен частному модулей числителя и знаменателя,
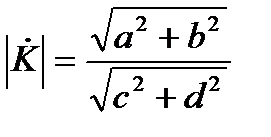, (4.3)
а ее аргумент – разности аргументов числителя и знаменателя,
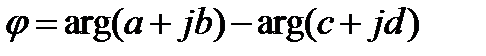. (4.4)
Аргумент комплексного числа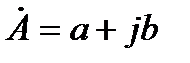 
определяется выражением
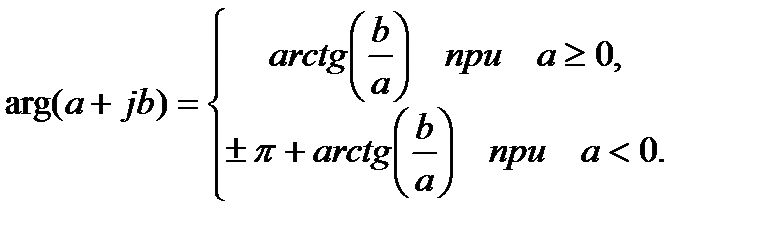(4.5)
Численные значения АЧХ безразмерны, а ФЧХ измеряется в угловых единицах (радианах или градусах).
В инженерной практике широко используется измерение АЧХ в децибелах (дБ).
Если рассматриваются модули коэффициентов 
передачи напряжения или тока, то их значение в децибелах равно
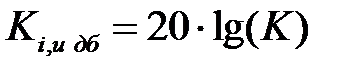. (4.6)
Если же речь идет о коэффициенте передачи мощности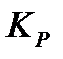 
, то
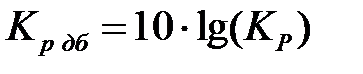. (4.7)
Логарифмическая мера АЧХ весьма удобна при анализе четырехполюсников.
Если 
, то получим, что 
дБ и амплитуда сигнала не меняется при прохождении через четырехполюсник.
Если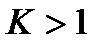 
, то 
и происходит усиление сигнала, а если наоборот, то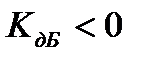 
и наблюдается ослабление (затухание) сигнала.
Основным достоинством логарифмической меры является возможность отображать графически широкий диапазон изменения АЧХ от маленьких величин 
или 
дБ до больших значений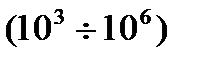 
или 
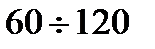дБ.
Измерение коэффициентов передачи в децибелах удобно при их перемножении, например, при каскадном соединении согласованно нагруженных четырехполюсников (эти вопросы рассматриваются в дальнейшем), при этом значения в децибелах будут складываться.
Определим АЧХ и ФЧХ цепи, показанной на рис.3.1.
Для найденного комплексного коэффициента передачи по напряжению модуль (АЧХ) и аргумент (ФЧХ) соответственно равны
,
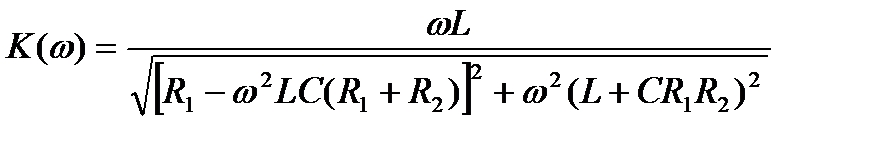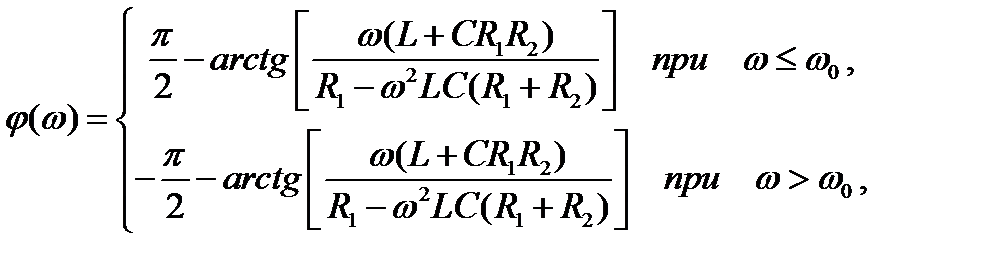
где
.
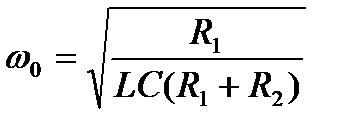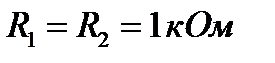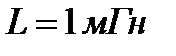На рис.4.1 показан график АЧХ четырехполюсника, показанного на рис.3.1 при 
, 
м и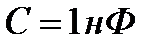 
.
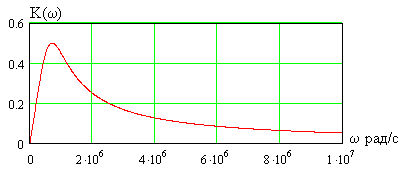
Рис. 4.1
Максимум АЧХ имеет место на частоте 
, в чем нетрудно убедиться, взяв производную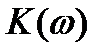 
и приравняв ее нулю.
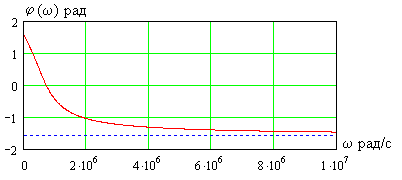
Рис. 4.2
На рис.4.2 приведен график ФЧХ четырехполюсника.
На частота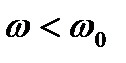х 
ФЧХ 
, то есть выходное напряжение опережает по фазе входное, а если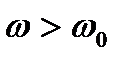 
, то наоборот.
На частоте 
сдвиг фаз между этими напряжениями равен нулю (они синфазны).
Рис. 4.3
На рис.4.3,а показана та же АЧХ, но в децибелах, а на рис.4.3,б – еще и в логарифмическом масштабе по оси частот.
Как видно, переход к логарифмическим масштабам по оси ординат (дБ) и оси частот позволяет разборчиво представить АЧХ в широком диапазоне значений.
Недостатком подобных графиков является искажение формы кривых по сравнению с равномерным масштабом.