При построении графика функции  удобно следовать следующей схеме.
удобно следовать следующей схеме.
1) Область определения функции.
2) Четность (нечетность), периодичность функции.
3) Точки пересечения графика с осями координат и промежутки, на которых  и
и  .
.
4) Стационарные и критические точки, промежутки возрастания и убывания функции, экстремумы.
5) Возможные точки перегиба, промежутки выпуклости вверх (вниз) функции.
6) Асимптоты графика.
7) График функции.
Примеры
6.1. Исследовать функцию:  и построить её график.
и построить её график.
n 1) Область определения функции:  . Точек разрыва нет.
. Точек разрыва нет.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 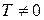 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
:  точки
точки  и
и  .
.
С осью  : точка
: точка  .
.
На всей области определения  функция
функция 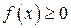 .
.
4) Найдём стационарные точки. Так как
 ,
,
то, решая уравнение:  , получаем
, получаем 
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| убывает |

| min
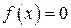
| |

| 
| возрастает |

| max

| |

| 
| убывает |

| min
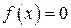
| |

| 
| возрастает |
5) Найдем возможные точки перегиба. Так как
 ,
,
то решением уравнения  будет
будет  .
.
Составим таблицу знаков второй производной

| 
| 
|

| 
| выпукла вниз |

| точка перегиба
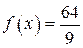
| |

| 
| выпукла вверх |

| точка перегиба
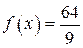
| |

| 
| выпукла вниз |
6) Так как у исследуемой функции нет точек разрыва и
 ,
,
то асимптот у графика нет.
7) Используя данные, полученные в п.п. 1-6, построим график функции.
 ƒ
ƒ
6.2. Исследовать функцию:  и построить её график.
и построить её график.
n 1) Область определения функции:  . Точек разрыва нет.
. Точек разрыва нет.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 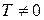 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
:  точки
точки  и
и  .
.
С осью  : точка
: точка  .
.
Функция  при
при  и
и  при
при  .
.
4) Найдём стационарные точки. Так как
 ,
,
то решая уравнение  , получаем стационарную точку
, получаем стационарную точку  . Кроме того, имеются две критических точки
. Кроме того, имеются две критических точки  и
и  в которых производная бесконечна.
в которых производная бесконечна.
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| убывает |

| 
| экстремума нет
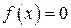
|

| 
| возрастает |

| min

| |

| 
| возрастает |

| 
| экстремума нет
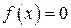
|

| 
| возрастает |
5) Найдем возможные точки перегиба. Так как
 ,
,
то возможными точками перегиба будут точки  и
и  .
.
Составим таблицу знаков второй производной

| 
| 
|

| 
| выпукла вверх |

| 
| точка перегиба
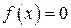
|

| 
| выпукла вниз |

| 
| точка перегиба
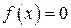
|

| 
| выпукла вверх |
6) Найдём асимптоты. Так как точек разрыва нет, и
 ,
,
то асимптот у графика функции нет.
7) Построим график функции

6.3. Исследовать функцию и построить её график.

n 1) Область определения функции:  .
.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 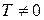 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
:  точек пересечения нет.
точек пересечения нет.
С осью  : точка
: точка  .
.
Функция  при
при  и
и  при
при  .
.
4) Найдем стационарные точки. Так как
 ,
,
то решая уравнение  , получаем стационарную точку
, получаем стационарную точку  . Кроме того, имеются две критических точки
. Кроме того, имеются две критических точки 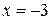 и
и  в которых производная не существует.
в которых производная не существует.
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| возрастает |

| не существует | разрыв 2 рода |

| 
| возрастает |

| точка максимума

| |

| 
| убывает |

| не существует | разрыв 2 рода |

| 
| убывает |
5) Найдем возможные точки перегиба. Так как
 ,
,
то точек перегиба нет, а промежутками постоянного направления выпуклости будут интервалы  ,
,  ,
,  .
.
Составим таблицу знаков второй производной.

| 
| 
|

| 
| выпукла вниз |

| 
| разрыв 2 рода |

| 
| выпукла вверх |

| 
| разрыв 2 рода |

| 
| выпукла вниз |
6) Найдём асимптоты.
Вертикальные: 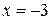 ,
,  , так как в этих точках функция имеет разрыв 2 рода.
, так как в этих точках функция имеет разрыв 2 рода.
Найдём наклонную асимптоту. Угловой коэффициент прямой  и число
и число  найдём, применяя формулы:
найдём, применяя формулы:
 ,
,
получаем горизонтальную асимптоту 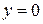 , наклонных асимптот нет.
, наклонных асимптот нет.
7) Построим график функции.
 ƒ
ƒ
6.4. Исследовать функцию и построить её график.
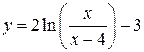
n 1) Область определения функции:  .
.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 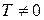 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
: 
 .
.
С осью  : точек пересечения нет.
: точек пересечения нет.
Функция  при
при  и
и  при
при  .
.
4) Найдем стационарные и критические точки. Вычисляя первую производную
 ,
,
находим критические точки  и
и 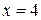 , в которых производная не существует.
, в которых производная не существует.
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| убывает |

| 
| разрыв 2 рода |

| не определена | не определена |

| 
| разрыв 2 рода |

| 
| убывает |
5) Найдем возможные точки перегиба. Так как
 ,
,
а точка  не принадлежит области определения, то будем два интервала постоянной выпуклости -
не принадлежит области определения, то будем два интервала постоянной выпуклости -  и
и  . При
. При 
 , поэтому функция выпукла вверх,
, поэтому функция выпукла вверх, 
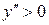 , поэтому функция выпукла вниз.
, поэтому функция выпукла вниз.
6) Найдём асимптоты.
Вертикальные:  , так как функция терпит разрыв в этих точках.
, так как функция терпит разрыв в этих точках.
Найдём наклонную (горизонтальную) асимптоту.
Угловой коэффициент прямой  и число
и число  найдём, применяя формулы:
найдём, применяя формулы:
 ;
;  .
.


Таким образом,  - горизонтальная асимптота.
- горизонтальная асимптота.
7) Построим график функции.
 ƒ
ƒ
6.5. Исследовать функцию и построить её график.

n 1) Область определения функции:  . Точек разрыва нет.
. Точек разрыва нет.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 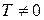 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
:  точка
точка  .
.
С осью  : точка
: точка  .
.
Функция  при
при  и
и  при
при  .
.
4) Найдём стационарные точки. Так как
 ,
,
то в точках  и
и  , производная не существует.
, производная не существует.
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| убывает |

| точка минимума

| |

| 
| возрастает |

| точка максимума

| |

| 
| убывает |
5) Найдем возможные точки перегиба. Так как
 ,
,
то в точках  и
и  , вторая производная
, вторая производная  не существует, а в точке
не существует, а в точке  она равна нулю.
она равна нулю.
Составим таблицу знаков второй производной.

| 
| 
|

| 
| выпукла вверх |

| не существует | |

| 
| выпукла вниз |

| ||

| 
| выпукла вверх |

| не существует | |

| 
| выпукла вниз |
6) Найдём асимптоты.
Вертикальных асимптот нет, так как функция определена на всей числовой оси.
Найдём наклонную асимптоту.
Угловой коэффициент прямой  и число
и число  найдём, применяя формулы:
найдём, применяя формулы:

 .
.
Таким образом, прямая 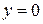 - горизонтальная асимптота.
- горизонтальная асимптота.
7) Построим график функции.

6.6. Исследовать функцию и построить её график.

n 1) Область определения функции:  . Точек разрыва нет.
. Точек разрыва нет.
2) Функция не четная, не нечетная  ,
,  , периодическая период
, периодическая период  .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  точек пересечения нет.
точек пересечения нет.
С осью  : точка
: точка 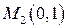 .
.
Функция  при
при  .
.
4) Найдём стационарные точки. Так как
 ,
,
то стационарными будут точки  ,
, 
Составим таблицу знаков производной и поведения функции на интервале  .
.

| 
| 
|

| 
| убывает |
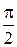
| точка минимума

| |

| 
| возрастает |

| точка максимума

| |

| 
| убывает |
Таким образом, точки  - точки минимума, а
- точки минимума, а  - точки максимума. На интервалах
- точки максимума. На интервалах  функция убывает, а на интервалах
функция убывает, а на интервалах 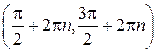 функция убывает (
функция убывает ( ).
).
5) Найдём возможные точки перегиба.
 .
.
Тогда корнями уравнения  будут точки
будут точки 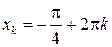 ,
,  ,
,  .
.
Составим таблицу знаков второй производной на интервале  .
.

| 
| 
|
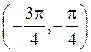
| 
| выпукла вверх |

| точка перегиба

| |
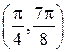
| 
| выпукла вниз |
Таким образом, точки 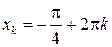 ,
,  - точки перегиба,
- точки перегиба,
6) Асимптоты отсутствуют.
7) Построим график функции
 ƒ
ƒ
6.6. Исследовать функцию и построить её график
 .
.
n 1) Область определения функции:  . Точка
. Точка  - точка разрыва 2 рода.
- точка разрыва 2 рода.
2) Функция общего вида (т.е. ни нечетная, ни четная, непериодическая), т.к.  ,
,  ,
,  при
при 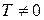 .
.
3) Найдём точки пересечения графика функции с осями координат.
С осью  :
:  точки пересечения
точки пересечения  ,
,  .
.
С осью  : точка
: точка  . Функция
. Функция  при
при 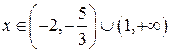 и
и  при
при  .
.
4) Найдем стационарные точки. Так как
 ,
,
то решая уравнение  , получаем стационарные точки
, получаем стационарные точки 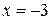 и
и  . Кроме того, имеется еще одна критическая точка
. Кроме того, имеется еще одна критическая точка  в которой производная не существует.
в которой производная не существует.
Составим таблицу знаков производной и поведения функции.

| 
| 
|

| 
| возрастает |

| точка максимума

| |

| 
| убывает |

| 
| точка разрыва 2 рода |

| 
| убывает |

| точка минимума | |

| 
| возрастает |
5) Найдем возможные точки перегиба. Так как
 ,
,
то точек перегиба нет, а промежутками постоянного направления выпуклости будут интервалы 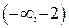 ,
, 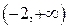 .
.
Составим таблицу знаков второй производной.

| 
| 
|
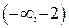
| 
| выпукла вверх |

| 
| разрыв 2 рода |

| 
| выпукла вниз |
6) Найдём асимптоты.
Вертикальная:  , так как в этой точке функция имеет разрыв 2 рода.
, так как в этой точке функция имеет разрыв 2 рода.
Найдём наклонную асимптоту. Угловой коэффициент прямой  и число
и число  найдём, применяя формулы:
найдём, применяя формулы:
 ,
, 
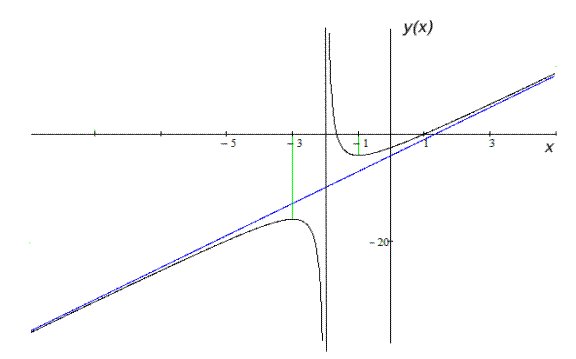
получаем наклонную асимптоту  , горизонтальных асимптот нет.
, горизонтальных асимптот нет.
7) Построим график функции.
 ƒ
ƒ