Кафедра гуманитарных и естественнонаучных дисциплин
А.Б. ДЮБУА, С.Н. МАШНИНА
МатематиЧЕСКИЙ АНАЛИЗ: исследование
Функций одной переменной
Допущено учебно-методическим советом Рязанского филиала
государственного образовательного учреждения высшего профессионального образования «Московский государственный университет экономики, статистики и информатики (мэси)» в качестве учебного пособия для студентов Рязанского филиала МЭСИ, обучающихся по специальностям:
080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухгалтерский учет, анализ и аудит»;080105 – «Финансы и кредит».
Протокол № 3 от 19 января. 2011 г.
Рязань 2011
УДК 517.2
ББК 22.15
Д11
Рецензент:
каф. высшей математики Рязанского государственного радиотехнического университета (зав. каф. К.В. Бухенский, к.ф.-м.н., доцент).
Дюбуа А.Б., Машнина С.Н. Математический анализ: исследование функций с помощью производных, – Рязань: Рязанский филиал МЭСИ, 2011 г. – 48 с.
Составлено в соответствии с Государственным образовательным стандартом по высшей математике для специальностей: 080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухгалтерский учет, анализ и аудит»; 080105 – «Финансы и кредит».
| © Рязанский филиал ГОУВПО «Московский государственный университет экономики, статистики и информатики (МЭСИ)», 2011 |
Возрастание и убывание функции.
Для того чтобы дифференцируемая на интервале 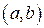 функция
функция  была возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялось условие
была возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялось условие
 при всех
при всех  .
.
Аналогично, условие
 при всех
при всех 
является необходимым и достаточным для убывания дифференцируемой на интервале 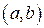 функции
функции  .
.
Примеры
1.1. Доказать, что функция  строго возрастает на промежутке
строго возрастает на промежутке  .
.
n Так как
 ,
,
то для всех  функция
функция  является строго возрастающей на всей области определения.ƒ
является строго возрастающей на всей области определения.ƒ
1.2. Доказать, что если  , то
, то  .
.
n Пусть  , тогда
, тогда  . Эта функция дифференцируема на интервале
. Эта функция дифференцируема на интервале  , причем
, причем
 ,
,
то для всех  функция
функция  строго убывает на интервале
строго убывает на интервале  . Поэтому
. Поэтому

для всех  .
.
То есть выполнено


 .ƒ
.ƒ
Экстремумы функции.
Необходимое условие экстремума.
Точки экстремума функции  следует искать среди тех точек области определения, в которых производная этой функции либо равна нулю, либо не существует. Точки, в которых производная данной функции равна нулю, называет стационарными точками этой функции, а точки, в которых функция непрерывна, а её производная либо равна нулю либо не существует,— ее критическими точками.
следует искать среди тех точек области определения, в которых производная этой функции либо равна нулю, либо не существует. Точки, в которых производная данной функции равна нулю, называет стационарными точками этой функции, а точки, в которых функция непрерывна, а её производная либо равна нулю либо не существует,— ее критическими точками.
Достаточные условие экстремума.
1) Если  меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку  , то
, то  - точка строгого минимума функции
- точка строгого минимума функции  . Если
. Если  меняет знак с плюса на минус при переходе через точку
меняет знак с плюса на минус при переходе через точку  , то
, то  - точка строгого максимума функции
- точка строгого максимума функции  .
.
2) Пусть  и существует вторая производная
и существует вторая производная  . Тогда, если
. Тогда, если  , то
, то  - точка строгого минимума функции
- точка строгого минимума функции  . Если
. Если 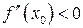 , то
, то  - точка строгого максимума функции
- точка строгого максимума функции  .
.
Примеры
2.1. Найти точки экстремума функции
 .
.
n Функция дифференцируема на множестве всех действительных чисел, поэтому все её точки экстремума содержатся среди стационарных точек функции, являющихся корнями уравнения  , т.е. уравнения
, т.е. уравнения
 ,
,
которое имеет корни  ,
,  ,
,  . Для удобства составим таблицу:
. Для удобства составим таблицу:

| 
| 
|

| 
| возрастает |

| ||

| 
| возрастает |

| max | |

| 
| убывает |

| min | |

| 
| возрастает |
Из таблицы видно, что  ,
,  - точки строгого максимума и минимума, а
- точки строгого максимума и минимума, а  не является точкой экстремума. ƒ
не является точкой экстремума. ƒ
2.2. Найти точки экстремума функции
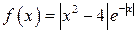 .
.
n Прежде всего, отметим, что функция  — четная, непрерывная на
— четная, непрерывная на  , дифференцируемая на
, дифференцируемая на  , кроме точек
, кроме точек  . Эквивалентное представление функции:
. Эквивалентное представление функции:
 .
.
Производная функции  равна
равна
 ,
,
критическими точками которой будут  ,
,  ,
,  .
.
Составим таблицу

| 
| 
|

| 
| возрастает |

| max | |
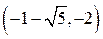
| 
| убывает |

| не существует | min |

| 
| убывает |

| не существует | max |

| 
| убывает |

| не существует | min |

| 
| возрастает |

| max | |

| 
| убывает |
Используя полученные результаты, получаем:  и
и  — точки строгого минимума функции
— точки строгого минимума функции  ,
,  ,
,  и
и 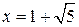 — точки строгого максимума этой функции.ƒ
— точки строгого максимума этой функции.ƒ
Наибольшее и наименьшее значения функции.
Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и имеет максимумы в точках
и имеет максимумы в точках  ,
,  ,….,
,….,  и минимумы в точках
и минимумы в точках  ,
,  ,…,
,…,  и не имеет других точек экстремума. Тогда наибольшее значение функции
и не имеет других точек экстремума. Тогда наибольшее значение функции  на отрезке
на отрезке  равно наибольшему из чисел
равно наибольшему из чисел  ,
,  ,
,  ,….,
,….,  ,
,  , а наименьшее этой функции на отрезке
, а наименьшее этой функции на отрезке  равно наименьшему из чисел
равно наименьшему из чисел  ,
,  ,
,  ,….,
,…., 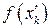 ,
,  .
.
Примеры
3.1. Найти наибольшее и наименьшее значение функции

на отрезке  .
.
n Как следует из примера 2.1. функция  на отрезке
на отрезке  имеет строгий максимум в точке
имеет строгий максимум в точке  и строгий минимум в точке
и строгий минимум в точке  . Следовательно, наибольшее значение функции
. Следовательно, наибольшее значение функции  на отрезке
на отрезке  равно
равно
 ,
,
а наименьшее
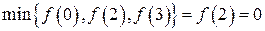 .ƒ
.ƒ
3.2. Найти наибольшее и наименьшее значение функции
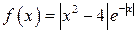
на отрезке  .
.
n Как следует из примера 2.2. функция  на отрезке
на отрезке  имеет строгий максимум в точках
имеет строгий максимум в точках  и
и 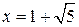 и строгий минимум в точке
и строгий минимум в точке  . Следовательно, наибольшее значение функции
. Следовательно, наибольшее значение функции  на отрезке
на отрезке  равно
равно
 ,
,
а наименьшее
 .ƒ
.ƒ
3.3. Корабль стоит на якоре в 10 км от ближайшей точки берега, матросу необходимо добраться до лагеря расположенного в 15 км вдоль берега. В каком точке берега должен пристать матрос, чтобы попасть в лагерь в ближайшее время? Скорость матроса на веслах 4 км/час, пешком 5 км/час.
 n Свяжем условие задачи с декартовой системой координат. Пусть корабль находится в точке
n Свяжем условие задачи с декартовой системой координат. Пусть корабль находится в точке  , лагерь в точке
, лагерь в точке  , точка
, точка 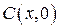 - место высадки матроса. Тогда суммарное время, необходимое матросу, для того, чтобы добраться из
- место высадки матроса. Тогда суммарное время, необходимое матросу, для того, чтобы добраться из  в
в 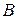 будет равно
будет равно  .
.
Таким образом задача сводится к нахождению минимума функции
 .
.
Находя производную, получаем
 .
.
Решая уравнение  , находим стационарную точку
, находим стационарную точку  . Следовательно, наименьшее значение функции на отрезке
. Следовательно, наименьшее значение функции на отрезке  равно
равно
 .ƒ
.ƒ
3.4. Из сектора радиуса  свертывается конус. При каком центральном угле
свертывается конус. При каком центральном угле  он имеет наибольший объем?
он имеет наибольший объем?
n Объем конуса вычисляется по формуле  , где
, где  - площадь круга - основания конуса,
- площадь круга - основания конуса, 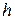 - его высота. Пусть
- его высота. Пусть  - длина окружности основания конуса, очевидно, она равна длине дуги исходного сектора, т.е.
- длина окружности основания конуса, очевидно, она равна длине дуги исходного сектора, т.е.  и
и  . Высота полученного конуса равна
. Высота полученного конуса равна
 ,
,
а его объем, как функция угла 
 .
.
Найдем стационарные точки функции  . Находя производную
. Находя производную
 ,
,
и решая уравнение 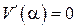 , получаем
, получаем  . Нетрудно убедиться, что при данном значении угла, объем конуса будет максимальным.ƒ
. Нетрудно убедиться, что при данном значении угла, объем конуса будет максимальным.ƒ
3.5. Найти положительное число, сумма которого и обратного к нему является наименьшей.
n Обозначим искомое число через  . Исследуем функцию
. Исследуем функцию
 .
.
Вычислим производную:  .
.
Производная имеет смысл для всех  , кроме
, кроме  . Критические точки функции:
. Критические точки функции:  Так как число положительное, имеем лишь одну точку для решения:
Так как число положительное, имеем лишь одну точку для решения:  . Найдём значение функции для
. Найдём значение функции для  . Слева от точки
. Слева от точки  производная отрицательная, справа – положительная. Значит, точка
производная отрицательная, справа – положительная. Значит, точка  - точка минимума.
- точка минимума.
Используем второе достаточное условие экстремума. Для этого найдём вторую производную:
 .
.
Найдём значение второй производной в критической точке  :
: 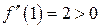 . Следовательно, это значение наименьшее. Поэтому:
. Следовательно, это значение наименьшее. Поэтому:  . ƒ
. ƒ
3.6. Во дворе детского садика надо огородить прямоугольной формы цветник, прилегающий к забору, длина которого больше 40 метров. Есть 200 плит, каждая из которых имеет длину 40 см. Каким должны быть размеры цветника, чтобы его площадь была наибольшей?
n Пусть  - длина одной стороны цветника, параллельной забору,
- длина одной стороны цветника, параллельной забору,  - длина смежной стороны цветника. Тогда:
- длина смежной стороны цветника. Тогда:  . По условию задачи длина изгороди:
. По условию задачи длина изгороди: 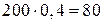 м. Следовательно,
м. Следовательно,
 ;
;
 ;
;
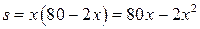 ;
;
 .
.
Найдём критические точки функции  .
.
 ;
;
 .
.
Найдём наибольшее значение функции  на отрезке
на отрезке  .
.
 ;
;
 ;
;
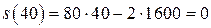 .
.
Получили, что наибольшее значение функции при  .
.
Таким образом, цветник будет иметь наибольшую площадь, если сторона, прилегающая к забору, вдвое больше другой.
Найдём вторую производную:
 .
.
Так как вторая производная отрицательная, значит,  - точка максимума.ƒ
- точка максимума.ƒ
3.7. Из пункта А в направлении к пункту В отправляется грузовой автомобиль со скоростью  км/ч. Одновременно из пункта В со скоростью 60км/ч отправляется автобус в направлении, перпендикулярном АВ. В какой момент времени от начала движения расстояние между машинами будет наибольшим,
км/ч. Одновременно из пункта В со скоростью 60км/ч отправляется автобус в направлении, перпендикулярном АВ. В какой момент времени от начала движения расстояние между машинами будет наибольшим,
n В момент времени t расстояние между машинами равно ЕС.
 – расстояние, которое прошла грузовая машина. Тогда:
– расстояние, которое прошла грузовая машина. Тогда:
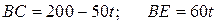 .
.
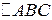 - прямоугольный. Применяя теорему Пифагора, имеем:
- прямоугольный. Применяя теорему Пифагора, имеем:

 .
.
Так как машины двигались не меньше 4 часов, то искать наименьшее значение функции будем на отрезке  .
.
Найдём производную

 .
.
Найдём критические точки функции:
 ;
;  ;
;  ч.
ч.
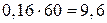 минуты.
минуты.
 Найдём значения функции в критических точках:
Найдём значения функции в критических точках:
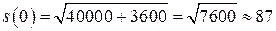 .
.
 ;
;
 в момент времени
в момент времени  часа. ƒ
часа. ƒ
3.8. На малом предприятии производят продукцию одного вида. Затраты на производство  единицы (в у. е.) выражаются формулой:
единицы (в у. е.) выражаются формулой:
 .
.
Доход, полученный от её реализации:
 .
.
Определите, какое количество продукции надо произвести, чтобы прибыль от её реализации была максимальной?
n Прибыль от реализации товара определяется разностью между доходом и затратами:
 .
.
Для нашей задачи:
 .
.
Для нахождения точки максимума функции 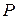 применим необходимое условие существования экстремума функции:
применим необходимое условие существования экстремума функции:
 или
или 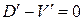 .
.
Последнее условие имеет экономический смысл: для того, чтобы прибыль была максимальной, необходимо, чтобы предельный доход  .
.
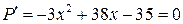 ;
;
 ;
;
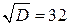 ;
;
 ;
;
 .
.
Находим:
 - наибольшая прибыль.
- наибольшая прибыль.
Значит, надо произвести 11,7 единиц продукции.