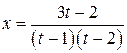 ,
, 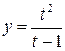
И построить ее.
n Найдем производные функции:

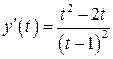 .
.
Рассмотрим промежутки монотонности функций  и
и  :
:

| 
| 
|
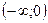
| убывает от 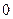 до до 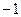
| возрастает от  до до 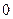
|

| возрастает от 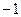 до до 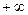
| убывает от 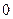 до до 
|

| возрастает от  до до 
| убывает от 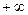 до до 
|

| убывает от  до до 
| убывает от  до до 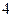
|

| убывает от 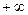 до до 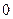
| возрастает от 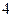 до до 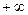
|
Если 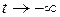 , то
, то 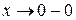 ,
,  ; значит
; значит  — вертикальная асимптота, можно предположить, что кривая выпукла вверх (к асимптоте).
— вертикальная асимптота, можно предположить, что кривая выпукла вверх (к асимптоте).
Точка  при
при  является точкой минимума функции
является точкой минимума функции  и точкой минимума функции
и точкой минимума функции  .
.
Если 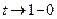 , то
, то  ,
,  . Следовательно, исследуем наклонную асимптоту.
. Следовательно, исследуем наклонную асимптоту.
 .
.
 .
.
Асимптота 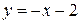 при
при  , причем
, причем  .
.
В достаточно малой левой полуокрестности точки  определим знак выражения:
определим знак выражения:
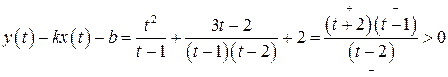 .
.
Следовательно, кривая расположена выше асимптоты и, можно предположить, что выпукла вниз.
Аналогично, если  , то
, то 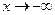 ,
,  ,
,
 ,
,
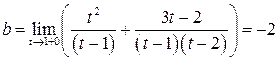 .
.
Асимптота 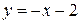 при
при  , причем
, причем 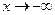 .
.
В достаточно малой правой полуокрестности точки 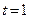 определим знак выражения:
определим знак выражения:
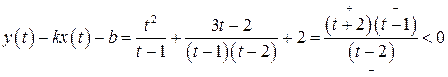 .
.
Следовательно, кривая расположена ниже асимптоты и, можно предположить, что выпукла вверх.
При 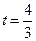 функция
функция  имеет максимум, а функция
имеет максимум, а функция  убывает при
убывает при 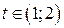 . Поэтому
. Поэтому 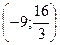 — точка максимума функции..
— точка максимума функции..
Если  , то
, то 
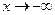 ,
,  . Следовательно,
. Следовательно,  — горизонтальная асимптота при
— горизонтальная асимптота при 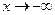 . Так как кривая расположена выше асимптоты, можно предположить, что она выпукла вниз (к асимптоте).
. Так как кривая расположена выше асимптоты, можно предположить, что она выпукла вниз (к асимптоте).
Если 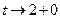 , то
, то 
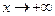 ,
,  . Следовательно,
. Следовательно,  — горизонтальная асимптота при
— горизонтальная асимптота при 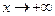 . Так как кривая расположена выше асимптоты, можно предположить, что она выпукла вниз (к асимптоте).
. Так как кривая расположена выше асимптоты, можно предположить, что она выпукла вниз (к асимптоте).
Если 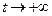 , то
, то  ,
,  . Значит
. Значит  — вертикальная асимптота. Можно предположить, что кривая выпукла вниз (к асимптоте).
— вертикальная асимптота. Можно предположить, что кривая выпукла вниз (к асимптоте).
Построим график

Задачи для самостоятельного решения
Задача 1. Построить графики функций с помощью производной первого порядка.
1. 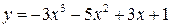 
| 2. 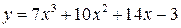
|
3. 
| 4. 
|
5. 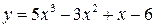
| 6. 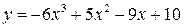
|
7. 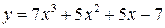
| 8. 
|
9. 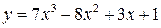
| 10. 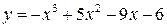
|
11. 
| 12. 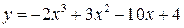
|
13. 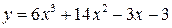
| 14. 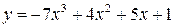
|
15. 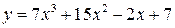
| 16. 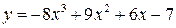
|
17. 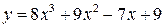
| 18. 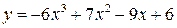
|
19. 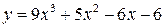
| 20. 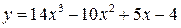
|
21. 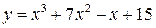
| 22. 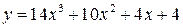
|
23. 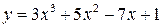
| 24. 
|
25. 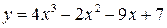
| 26. 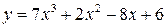
|
27. 
| 28. 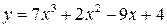
|
29. 
| 30. 
|
Задача 2. Найти наибольшее и наименьшее значения функций на заданных отрезках.
1. 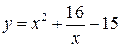 , , 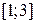 . .
| 2.  
|
3. 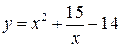 , , 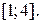
| 4. 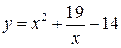 , , 
|
5. 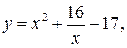 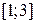 . .
| 6.  , , 
|
7.  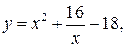 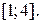
| 8. 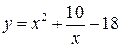 , , 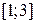
|
9.  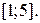
| 10.  , , 
|
11. 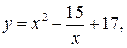 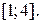
| 12.  , , 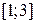
|
13.  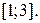
| 14.  , , 
|
15. 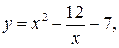 
| 16.  , , 
|
17. 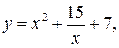 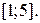
| 18.  , , 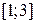
|
19. 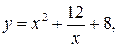 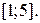
| 20. 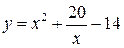 , , 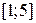
|
21. 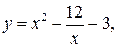 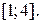
| 22. 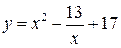 , , 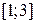
|
23.  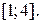
| 24. 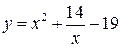 , , 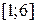
|
25. 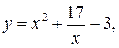 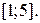
| 26. 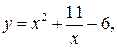 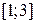
|
27. 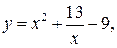 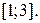
| 28. 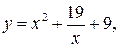 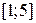
|
29. 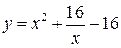 , , 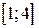 . .
| 30.  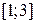
|
Задача 3. Провести полное исследование функций и построить их графики
1.  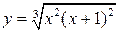
| 2.  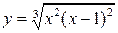
|
3. 
| 4. 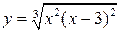
|
5. 
| 6. 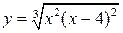
|
7. 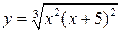
| 8. 
|
9. 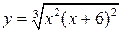
| 10. 
|
11. 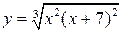
| 12. 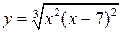
|
13. 
| 14. 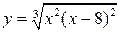
|
15. 
| 16. 
|
17. 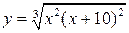
| 18. 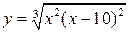
|
19. 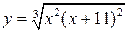
| 20. 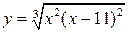
|
21. 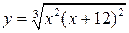
| 22. 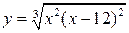
|
23. 
| 24. 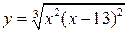
|
25. 
| 26. 
|
27. 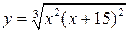
| 28. 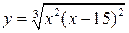
|
29. 
| 30. 
|
Задача 4. Провести полное исследование функций и построить их графики
1. 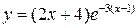
| 2. 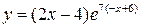
|
3. 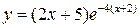
| 4. 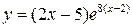
|
5. 
| 6. 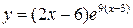
|
7. 
| 8. 
|
9. 
| 10. 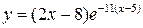
|
11. 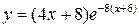
| 12. 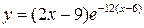
|
13. 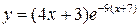
| 14. 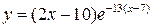
|
15. 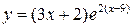
| 16. 
|
17. 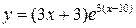
| 18. 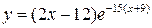
|
19. 
| 20. 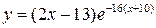
|
21. 
| 22. 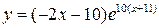
|
23. 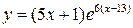
| 24. 
|
25. 
| 26. 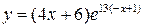
|
27.  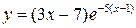
| 28. 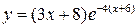
|
29. 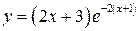
| 30. 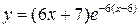
|
Задача 5. Провести полное исследование функций и построить их графики
1. 
| 2. 
|
3. 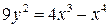
| 4. 
|
5. 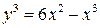
| 6. 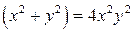
|
7. 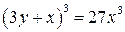
| 8. 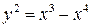
|
9. 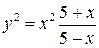
| 10. 
|
11. 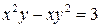 
| 12. 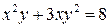
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 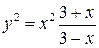
|
19. 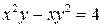
| 20. 
|
21. 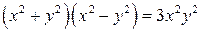
| 22. 
|
23. 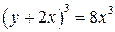
| 24. 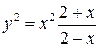
|
25. 
| 26. 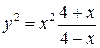
|
27. 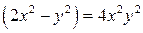
| 28. 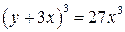
|
29. 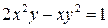
| 30. 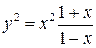
|
Задача 6. Провести полное исследование функций и построить их графики
1. 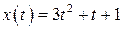 , , 
| 2. 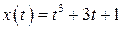 , , 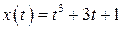
|
3. 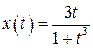 , , 
| 4.  , , 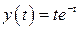
|
5.  , , 
| 6.  , , 
|
7. 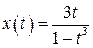 , , 
| 8. 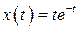 , , 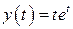
|
9. 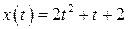 , , 
| 10.  , , 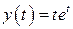
|
11. 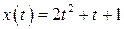 , , 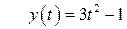
| 12. 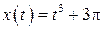 , , 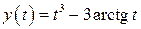
|
13. 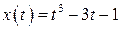 , , 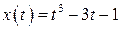
| 14.  , , 
|
15. 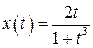 , , 
| 16. 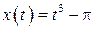 , , 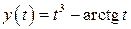
|
17.  , , 
| 18. 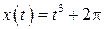 , , 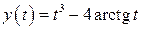
|
19. 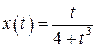 , , 
| 20. 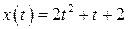 , , 
|
21. 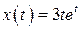 , , 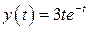
| 22. 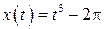 , , 
|
23. 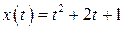 , , 
| 24.  , , 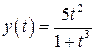
|
25.  , , 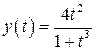
| 26. 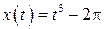 , , 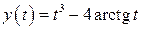
|
27. 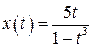 , , 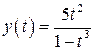
| 28. 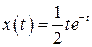 , , 
|
29. 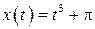 , , 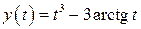
| 30. 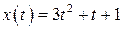 , , 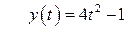
|
Литература
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977.
2. Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. – М.: Высшая школа, 2000.
3. Зорич В.А. Математический анализ.– М.: Наука, 1981.
4. Кудрявцев Л.Д. Курс математического анализа.– М.: Высшая школа, 1981.
5. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. – М.: Наука, 1977.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: ФИЗМАТЛИТ, 2002.
СОДЕРЖАНИЕ
1. Возрастание и убывание функции…………………………….………………...3
2. Экстремумы функции…………………………………………….……………...4
3. Наибольшее и наименьшее значение функции…………………….…………..6
4. Выпуклость функции и точки перегиба……………………………….………13
5. Асимптоты………………………………………………………………….…...16
6. Построение графиков функции…………………………………………….......21
Задачи для самостоятельной работы…………………….………………………..39
Литература…………………………………………………………………………..46
Учебное издание
Александр Борисович Дюбуа