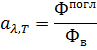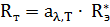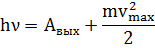Методические указания по выполнению РГР

Методические указания по выполнению РГР

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И

КВАНТОВАЯ МЕХАНИКА

 

 

530.145 (076.5)

М 348

министерство энергетики И УГОЛЬНОЙ

ПРОМЫШЛЕННОСТИ украины

СЕВАСТОПОЛЬСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

ЯДЕРНОЙ ЭНЕРГИИ И ПРОМЫШЛЕННОСТИ

О.В. Матузаева, Т.И. Гарматенко,

Е.В. Мирошниченко

 

Тепловое излучение иКвантовая механика

 

методические рекомендации по выполнению РГР

У т в е р ж д е н о

Ученым советом университета

Севастополь

УДК.530.145:535.1 (076.5)

530.145 (076.5)

М 348

 

О.В. Матузаева, Т.И. Гарматенко, Е.В. Мирошниченко

 

М 348 Тепловое излучение и квантовая механика:учебник-методичка. Пособие. – Ч. 2. – Севастополь: СНУЯЭиП, 2012. - с.: ил.

 

Предназначена для студентов II курса. Данное пособие включает в себя набор задач, которые полностью отражают содержание 3 семестра курса по физике по теме “Тепловое излучение. Квантовая механика”. Эти задачи предлагают для самостоятельной проработки студентами II курса очной формы обучения всех специальностей с последующей защитой у преподавателя.

Методичка изложения, характер и содержание предлагаемых задач позволяет рекомендовать пособие и для проведения практических занятий, самостоятельной работы и подготовке к экзамену по дисциплине “Физика”.

Рецензенты: доктор ф-м наук Л.В. Третьякова

к.ш.н, доцент Рипп А.Г

доцент И.Б. Стаценко

 

 

ПРЕДИСЛОВИЕ

Созданное к концу прошлого столетия здание классичес­кой физики было очень стройным. Однако в нем начали прояв­ляться слабые места. Одним из слабых мест классической физики явилась теория излучения абсолютно черного тела. Попытки построить её с помощью классических законов оказа­лись безуспешными. Дня того, чтобы решить эту проблему, пришлось коренным образом пересмотреть сложившиеся, при­вычные представления и ввести понятия, чуждые духу класси­ческой физики. Введя представление об испускании и погло­щении света отдельными порциями - квантами, Макс Планк в 1900 году решил задачу об излучении абсолютно черного тела. Таким образом, на пороге XX столетия появилось поня­тие кванта.

В 1905 г. А. Эйнштейн пошел дальше Планка. Не ограничи­ваясь постулатом квантовых свойств процессов поглощения и излучения, он предложил считать, что такие свойства при­сущи свету вообще. В соответствии с гипотезой световых квантов (фотонов), выдвинутой Эйнштейном, свет состоит из квантов (корпускул), несущих порцию энергии и летящих со скоростью света. Гипотеза световых квантов позволила Эйн­штейну объяснить, например, фотоэлектрический эффект - - явление, которое вряд ли может быть объяснено волновой теорией света.

Начало XX века характеризуется настойчивыми попытка­ми проникнуть во внутреннее строение атомов. Открытие ядра позволило Резерфорду разработать модель атома, в котором электроны вокруг ядра вращаются подобно тому, как движутся планеты вокруг Солнца. Однако такая модель не могла объяс­нить ряд экспериментальных фактов.

Излучение водородного атома имеет вид бесконечной последовательности резко выраженных спектральных линий. В атоме водорода имеется лишь один вращающийся вокруг яд­ра электрон. По законам электродинамики такой электрон должен непрерывно излучать, а стало быть терять энергию. Поэтому в процессе движения он обязан был бы неизбежно приближаться к ядру всё ближе и ближе и в конце концов упасть на него. Первоначально электрон, обладая какой-то определённой частотой, должен излучать свет именно этой частоты. Когда частота его движения плавно изменится из-за энергетических потерь, должна измениться и частота излучения. Это противоречит опытному спектру поглощения водорода, состоящего из отдельных линий поглощения.

Первый разительный успех в объяснении наблюдаемых спектров принесла теория атома, развитая Нильсом Бором в 1913 г. Однако эта теория носила явные черты непоследова­тельности: наряду о подчинением движения электрона в ато­ме законам классической механики она налагала на это дви­жение специальные квантовые ограничения. За эту непоследо­вательность теории вскоре пришлось расплатиться. После первых успехов в объяснении спектра простейшего атома - - водорода - обнаружилась неспособность теории Бора объ­яснить поведение атомов с двумя и большим числом Электро­нов.

Назрела необходимость создания новой целостной теории атомов. Начало созданию такой теории было положено в 1924г. гипотезой Луи де Бройля о том, что частицы вещества долж­ны обнаруживать при определенных условиях волновые свойст­ва. Опытное подтверждение этой гипотезы создало предпосыл­ки для создания новой физической теории- волновой или квантовой механики. Квантовая механика достигла порази^ тельных успехов в объяснении атомных процессов и строения вещества.

Каково же соотношение между квантовой и классической механикой? Квантовая механика является более общей теорией, чем механика Ньютона. Последняя содержится в ней как приб­лиженный предельный случай. Квантовая механика переходит в механику Ньютона в случае тел достаточно больших масс. Поэтому механика Ньютона, как и вся классическая физика, своего значения не утратила.

Тепловое излучение –электромагнитное излучение, испускаемое веществом и возникающее за счет его внутренней энергии.

ОСНОВНЫЕ ФОРМУЛЫ

 

 

· Характеристики теплового излучения: Энергетическая Светимость спектральная плотность энергетической светимости	Обозначения и наименования физических величин · Rэ - энергетическая светимость тела; · Rэ* - энергетическая светимость а.ч.т. (абсолютно черное тело); · S – площадь поверхности излучателя; · Wизл – энергия излучения; · t – время излучения; · Фпогл – поток излучения поглощенный телом; · Ф0 – поток излучения, падающий на тело; · T – термодинамическая температура; · λm – длина волны, на которую приходится максимум энергии излучателя; · - максимальная спектральная. плотность энергетической светимости а.ч.т.; · - спектральная плотность энергетической светимости а.ч.т.;
· Параметры теплового излучения: Поглощательная способность тела мощность излучения   Формула энергетической светимости тела и энергетической светимостью а.ч.т. (абсолютно черное тело)
· Законы теплового излучения:   Закон Стефана- Больцмана Закон смещения Вина Второй закон …. Вина Закон Кирхгофа	· Физические постоянные   σ=5,67∙10-8 – постоянная … Стефана-Больцмана; b=2,9∙10-3 м∙К – постоянная Вина; С=1,3∙10-5 - постоянная, связывающая максимальную спектральную плотность энергетической светимости а.ч.т. с термодинамической температурой;

Внешний фотоэффект – явление вырывания электронов из вещества под действием падающего на него света.

· Характеристики фотона: E=h   E=mc2 энергия длина волны   масса Pr=mc импульс	Обозначения и наименования физических величин   · – частота света; · Qmax – максимальный заряд, переносимый. … фотоэлектронами; · n – число фотоэлектронов, вылетающих из освещаемого металла в единицу времени; · λкр – максимальная длина волны излучения, при которой еще возможен фотоэффект; · кр – минимальная частота излучения, при которой еще возможен фотоэффект; · Авых – работа выхода электрона из металла; · - кинетическая энергия электрона; · U3 – задерживающее напряжение;
· Параметры внешнего фотоэффекта: Сила тока Насыщения “Красная граница” фотоэффекта
· Законы внешнего фотоэффекта: /// Уравнение Эйнштейна   работа задерживающего поля	· Физические постоянные   h=6,62∙10-34 Дж∙с – постоянная Планка; с=3∙108 м/с – скорость света в вакууме; e=1,6∙10-19 Кл – заряд электрона; m=9,1∙10-31 кг – масса электрона;

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ОФОРМЛЕНИЮ ЗАДАЧ

1. Расчётно-графическую работу следует решать в отдельной тетради.

2. В тетради следует оставлять поля (30 мм) на каждой странице.

3. При решении задач следует начинать с новой страницы;

ü Каждую задачу следует начинать с новой страницы;

ü Указать номер задачи;

ü Написать полное условие задачи;

ü Ниже условия записать, с левой стороны, выписать все данные, имеющиеся в задаче;

ü Отделить выписанные данные вертикальной чертой и снова переписать их, но уже с системе СИ;

ü Сделать чертеж, поясняющий содержание задачи (аккуратно, используя чертежные принадлежности);

ü Решать задачу следует в буквенном виде до конечной формулы, не делать промежуточных вычислений;

ü Решения задач следует сопровождать краткими пояснениями;

ü Подставить данные условия задачи в итоговую формулу, ответ дать в численном виде.

Примеры решения задач

 

Пример 1. Во сколько раз увеличится мощность излучения абсолютно черного тела, если максимум энергии излучения пе­редвинется от красной границы (λ_кр = 0,76 мкм) видимого спек­тра к его фиолетовой границе (λ_ф = 0,38 мкм)?

Дано: λ_кр = 0,76 мкм = 7,6∙10^-7 м; λ_ф = 0,38 мкм = 3,8∙10^-7 м.

Найти: X =

Решение:

Длина волны, на которую при­ходится максимум энергии излу­чения абсолютно черного тела, определяется из закона смещения Вина:

λ_max =

где Т-термодинамическая температура излучателя

b= 2,9∙10^-3 м·К- постоянная Вина.

По формуле определяем температуру излучателя, соот­ветствующую красной и фиолетовой границам видимой области спектра:

T_кр = ; T_ф =

Мощность излучения абсолютно черного тела

Р = R_эS,

где R_э - энергетическая светимость абсолютно черного тела;

S- площадь поверхности излучающего тела.

В соответствии с законом Стефана-Больцмана

R_э = σT⁴,

где δ - постоянная Стефана-Больцмана. Тогда для красной и фиолетовой границ видимой области спектра

P_кр = σT⁴_крS, a P_ф = σT⁴_фS.

Следовательно.

X = = = ()⁴

Произведем вычисления:

X = ()⁴ = 2⁴ =16

Ответ: Мощность излучения увеличивается в 16 раз.

Пример 2. Определить с помощью формулы Планка энерге­тическую светимость ∆R_э, абсолютно черного тела, приходя­щуюся на узкий интервал длин волн ∆λ = 10А, соответствующий максимуму спектральной плотности энергетической светимости при температуре тела Т= 3000 К.

Дано: ∆λ = 10A = 10∙10^-10м; Т = 3000 К.

Найти: ∆R_э.

 

Решение:

 

Спектральная плотность энергетиче­ской светимости абсолютно черного тела характеризует распределение энергии в спектре излучения тела по длинам волн и выражается формулой r_λ,T = , где dR_э - энергетическая светимость, приходящаяся на интервал длин волн от λ до λ+dλ.

Отсюда следует, что ∆ = r_{λ,T ∙} ∆λ,

где r_λ,T = _∙ .

Используя закон смещения Вина λ₀ = ,формулу Планка можно записать так: r_λ,T = = ∙T⁵ ,

или r_λ,T = C∙T⁵.

Эту формулу называют вторым законом Вина.

Константа C = = 1,29∙10^-5

Тогда расчетная формула ∆ = r_λ0,T∙∆λ примет упрощенный вид:

∆ = С∙Т⁵∙∆λ

Подставив числовые значения величин, получим:

∆ =1,29∙10^-5t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/><w:vertAlign w:val="superscript"/></w:rPr><m:t>5</m:t></m:r></m:sup></m:sSup></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> ∙ (3000К)⁵∙10^-9м = 3,2∙10³

Ответ: ∆ ²

Пример 3. Давление света с длиной волны 0,55 мкм нормально падающего на зеркальную поверхность равно 9 мкПа. Опреде­лить концентрацию фотонов вблизи поверхности.

Дано: λ = 0,55 мкм; р=9 мкПа; ρ= 1.

Найти: n.

Решение, Давление света при нормальном падении на поверх­ность с коэффициентом отражения р определяется по формуле

ρ = 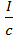(l+ρ) = w(l+ρ),

где I— интенсивность света; с — скорость света в вакууме; w — объемная плотность энергии излучения, w = I/c.

Объемная плотность энергии wравна произведению концент­рации фотонов п (числа фотонов в единице объема) на энергию одного фотона ε = hс/λ, т. е.

 

W =

где h — постоянная Планка; λ — длина волны света. Подставляя

P = (1+ρ)

Откуда

N =

 

Проводя вычисления, найдем

n = = 1,25∙10¹³м^-3

 

Ответ: n = 1,25 ∙ 10¹³ м^-3.

Пример 4. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потен­циалов, равной 1,5 В.

Дано: λ_к=0,257 мкм; U=1,5 В.

Найти: λ.

Решение. Согласно уравнению Эйнштейна для внешнего фото­эффекта

= A+W_max (1)

Где h -постоянная Планка, с -скорость света в вакууме; λ -длина волны света, А - работа выхода электронов из металла; W_max -максимальная кинетическая энергия фотоэлектронов.

Красная граница фотоэффекта определяется из условия равен­ства энергии фотона ε = hc/λ работе выхода электронов А, т. е.

= A (2)

Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов U:

W_max = eU, (3)

где е — элементарный заряд (заряд электрона).

Подставляя выражение (2) и (3) в (1), получим

= +eU

Из уравнения (4) найдем длину волны света:

λ = ( + )^-1

Подставляя в (5) числовые значения, получим

λ = ()^-1 = 1,96∙10^-7м = 0,196мкм

Ответ: λ = 0,196 мкм.

Пример 5. Определить максимальную скорость υ_max фото­электронов, вырываемых с поверхности серебра: 1) ультрафио­летовым излучением с длиной волны λ₁= 0,155 мкм; 2) ɣ-излучением с длиной волны λ₂=1 пм.

Дано: 1) λ₁ = 0,155 мкм =1,55∙10^-7м; 2) λ₂ = 1 пм =1∙10^-12м

Найти: υ_max-?

Решение:

Максимальную скорость фотоэлектронов можно опреде­лить из уравнения Эйнштейна для фотоэффекта:

ε = A+W_max

где ε = энергия фотонов, падающих на поверхность металла;

А - работа выхода электрона из металла;

W_max- максимальная кинетическая энергия фотоэлектро­нов.

 

Скорость фотоэлектрона зависит от энергии фотона, вызы­вающего фотоэффект: если энергия в фотона много меньше энергии покоя

Е₀- электрона, то кинетическую энергию фото­электрона можно найти по классической формуле:

W_max =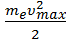

если же энергия ε фотона сравнима по величине с энергией по­коя Е₀ электрона, то кинетическую энергию фотоэлектронов не­обходимо вычислять по релятивистской формуле

W = E-E₀ = E₀(), где 𝛽 = .

Вычислим энергию фотона ультрафиолетового излучения по формуле:

ε₁= = Дж = 1,28∙10^-18 Дж,

 

или ε₁ = эВ.

Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (Е₀ = 0,51 МэВ). Следовательно, кинетическая энергия фотоэлектрона может быть выражена по классической формуле:

ε₁ = A+ , откуда υ_max = _,

где А = 7,5-10 ^-19 Дж = 4,7 эВ - работа выхода электронов из се­ребра.

Произведем вычисления:

υ_max= =1,08∙10⁶

Вычислим энергию фотона ɣ-излучения:

ε₂ = = Дж = 1,99∙10^-13Дж

или ε₂ = эВ =1,24∙10⁶эВ=1,24 МэВ

Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона рав­на энергии фотона:W_max= ε₂ = 1,24 МэВ. В данном случае для вычисления скорости фотоэлектрона следует взять релятивист­скую формулу кинетической энергии. Из этой формулы най­дем

𝛽 =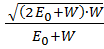

Заметив, что υ = c∙𝛽 и W_max = ε₂, получим

υ_max =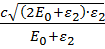

Произведем вычисления:

υ_max =

 

Ответ: 1) υ_max = 1,08∙10⁶ м/с; 2) υ_max = 2,85∙10⁸ м/с.