Тема 1: Тепловое излучения

Задачи

1. Уединенный цинковый шарик облучают монохромати­ческим светом длиной волны λ= 40 нм. Определите, до какого потенциала зарядится шарик. Работа выхода электронов из цин­ка A=4,0 эВ.

 

2. Во сколько раз увеличится поток излучения абсолютно черного тела, если максимум энергии излучения передвинется от красной границы (λ_к = 0,76 мкм) видимого спектра к его фиоле­товой границе λ_ф= 0,38 мкм)?

3. Какую мощность нужно подводить к свинцовому ша­рику радиусом r = 4 см, чтобы поддерживать его температуру t₁ = 27°С, если температура окружающей среды t₂ = -23°C? Счи­тать, что теплота теряется только вследствие излучения. Поглощательная способность свинца а_т=0,6.

4. Определите количество теплоты, теряемое поверхно­стью расплавленной платины при t° = 1770°С за t = 1 мин., если площадь поверхности S= 100 см. Коэффициент поглощения принять равным α= 0,8.

5. Максимум энергии излучения абсолютно черного тела приходится на длину волны λ = 450 нм. Определите температуру и энергетическую светимость тела.

 

6. Площадь поверхности нити накала 60-ваттной вольф­рамовой лампы накаливания S=0,5 см². Коэффициент поглоще­ния вольфрама а_т=0,6. Определите температуру нити накала.

7. Принимая спектр Солнца за спектр излучения абсо­лютно черного тела, определите мощность суммарного (инте­грального) (т.е. приходящегося на все длины волн) излучения,если максимум испускательной способности соответствует дли­не волны λ_тах ⁼ 0,48 мкм. Радиус Солнца считать равным R_c = 6,95∙10⁵ км.

8. Определите длину волны, соответствующую макси­мальной спектральной плотности энергетической светимости абсолютно черного тела равной (r_λ,T)_max= 4,16∙10¹¹ Вт/м³. Посто­янные Вина b = 2,9∙10^-3 м∙К; С = 1,3∙10⁵ Вт/м³∙К⁵.

9. Максимум спектральной плотности энергетической светимости (r_λ,T) яркой красноватой звезды Арктур приходится на длину волны λ=5800 А. Принимая, что звезда излучает как абсолютно черное тело, определите температуру поверхности звезды. (Необходимые постоянные см. задачу № 7).

10. Муфельная печь, потребляющая мощность Р - 1 кВт, имеет отверстие площадью S= 100 см². Определите долю ƞ мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна Т= 1 кК.

11. Средняя энергетическая светимость поверхности Земли равна R_e = 0,54 Дж/см²мин. Если условно считать, что Земля из­лучает как серое тело с коэффициентом черноты а_Т = 0,25, опре­делите длину волы λ_max, на которую приходится максимум энер­гии излучения.

12. Определите силу светового давления на зеркальную поверхность площадью S - 100 см², если интенсивность светово­го потока, падающего нормально на эту поверхность, равна Е_е = 2,5 кВт/м².

13. Определите давление на черную поверхность, созда­ваемое светом с длиной волны λ = 0,4 мкм, если ежесекундно на поверхность S= 1 см² падает n = 6∙10¹⁶ фотонов.

14. Световое давление, испытываемое зеркальной поверх­ностью площадью S = 1 см², равно р= 10^-6Па. Определите длину волны монохроматического света, если ежесекундно падает п = 5∙10¹² фотонов.

15. Определите давление света на стенки колбы электриче­ской лампы мощностью Р = 100 Вт. Колба лампы - сфера радиу­сом R= 5 см, стенки которой отражают 10% падающего на них света. Считать, что вся потребляемая лампой мощность идет на излучение.

16. Давление монохроматического света с длиной волны λ = 0,6 мкм на черную поверхность равно ρ = 10^-7 Па. Сколько фо­тонов падает ежесекундно на 1 м² поверхности?

17. Ежесекундно на зеркальную поверхность площадью S= 1м² нормально падает п = 15∙10²⁰ фотонов. Определите длину волны монохроматического света, если давление света на по­верхность р = 5 мкПа.

18. На зеркальную поверхность нормально падает моно­хроматический свет с длиной волны λ = 0,55 мкм. Поток излуче­ния Ф_е составляет 0,45 Вт. Определите: 1) число фотонов, па­дающих на поверхность за время t= 5 с; 2) силу давления, испы­тываемую этой поверхностью.

19. Точечный источник монохроматического (λ = 1 нм) из­лучения находится в центре сферической зачерненной колбы радиусом R = 10 см. Определите световое давление р, произво­димое на внутреннюю поверхность колбы, если мощность ис­точника Р = 1 кВт.

20. Параллельный пучок монохроматических лучей (λ= 0,5 мкм) падает на зачерненную поверхность и производит на нее давление ρ=10^-9 Н/см². Определите концентрацию n₀фотонов в световом пучке.

21.Давление света, производимое на зеркальную поверх­ность р= 5 мПа. Определите концентрацию n₀фотонов вблизи поверхности, если частота света, падающего на поверхность, v= 6∙10¹⁴ Гц.

22. Определить температуру Т, при которой энергетическая светимость R_эчерного тела равна 10 кВт/м².

23. Поток энергии Ф_e , излучаемый из смотрового окошка плавильной печи, равен 34 Вт. Определить температуру T печи, если площадь отверстия S=6см².

24. Определить энергию W, излучаемую за время t=l мин из смотрового окошка площадью S=8 см² плавильной печи, если ее температура T=1,2 кК.

25.Температура T верхних слоев звезды Сириус равна 10 кK. Определить поток энергии Ф_е, излучаемый с поверхности площадью S =1 км² этой звезды.

26. Определить относительное увеличение ∆R_э / R_ээнергетической светимости черного тела при увеличении его температуры на 1%.

27. Во сколько раз надо увеличить термодинамическую температуру черного тела, чтобы его энергетическая светимость R_э возросла в два раза?

28. Принимая, что Солнце излучает как черное тело, вычислить его энергетическую светимость R_э и температуру Т его поверхности. Солнечный диск виден с Земли под углом ϑ=32. Солнечная постоянная С=1,4кДж/(м² ∙с).

29. Определить установившуюся температуру T зачерненной металлической пластинки, расположенной перпендикулярно солнечным лучам вне земной атмосферы на среднем расстоянии от Земли до Солнца. Значение солнечной постоянной приведено в предыдущей задаче.

30. Принимая коэффициент теплового излучения ε угля при температуре T=600 K равным 0,8 определить: 1) энергетическую светимость R_э угля; 2)энергию W, излучаемую с поверхности угля с площадью S=5 см² за время t=10 мин.

31. С поверхности сажи площадью S=2 см² при температуре T=400 К за время 5 мин излучается энергия W=83Дж. Определить коэффициент теплового излучения ε сажи.

32. Муфельная печь потребляет мощность Р=1 кВт. Температура T ее внутренней поверхности при открытом отверстии площадью S=25 см² равна 1,2 кК. Считая, что отверстие печи излучает как черное тело, определить, какая часть со мощности рассеивается стенками.

33. Можно условно принять, что Земля излучает как серое тело, находящееся при температуре T=280 К. Определить коэффициент теплового излучения в Земли, если энергетическая светимость R_э ее поверхности равна 325 кДж/(м²∙ч)

34. Мощность Р излучения шара радиусом R=10 см при некоторой постоянной температуре T равна 1 кВт. Найти эту температуру, считая шар серым телом с коэффициентом теплового излучения ε =0,25.

35. На какую длину волны λ_m приходится максимум спектральной плотности энергетической светимости (r^*_λ,T)_max черного тела при температуре t=0°C?

36. Температура верхних слоев Солнца равна 5,3 кК. Считая солнце черным телом, определить длину волны λ_m, котором соответствует максимальная спектральная плотность энергетической светимости (r^*_λ,T)_max Солнца.

37. Определить температуру T черного тела, при которой максимум спектральной плотности энергетической светимости (r^*_λ,T)_max приходится на красную границу видимого спектра (λ₁ =750 нм); на фиолетовую (λ₂=380 нм).

38. Максимум спектральной плотности энергетической светимости (r^*_λ,T)_max яркой звезды Арктур приходится на длину волны λ_m =580 нм. Принимая, что звезда излучает как черное тело, определить температуру Т поверхности звезды.

39. Вследствие изменения температуры черного тела максимум спектральной плотности (r^*_λ,T)_max сместился с λ₁=2,4 мкм на λ₂=0,8 мкм. Как и во сколько раз изменилась энергетическая светимость R_э тела и максимальная спектральная плотность энергетической светимости?

40. При увеличении термодинамической температуры Т черного тела в два раза длина волны λ_m,на которую приходится максимум спектральной плотности энергетической светимости (r^*_λ,T)_max уменьшилась на ∆λ =400 нм. Определить начальную и конечную температуры Т₁ и Т₂.

41. Эталон единицы силы света - кандела - представляет собой полный (излучающий волны всех длин) излучатель, поверхность которого площадью S=0,5305 мм² имеет температуру t затвердевания платины, равную 1063° С. Определить мощность Р излучателя.

42. Максимальная спектральная плотность энергетической светимости (r^*_λ,T)_max черного тела равна 4,16∙10¹¹(Вт/м²)/м. На какую длину волны λ_mона приходится?

43. Температуру T черного тела равна 2 кK. Определить:r^* 1)спектральную плотность энергетической светимости (r^*_λ,T)_max для длины волны λ = 600 нм; 2) энергетическую светимость R_эв интервале длин волн от λ₁=590 нм до λ₂ =610 нм. Принять, что средняя спектральная плотность энергетической светимости тела в этом интервале равна значению, найденному для длины волны λ=600нм.

 

 

Тема 2: Фотоэффект

Задачи

1. Определите максимальную скорость υ_max фотоэлектрона, вырванного с поверхности платины (работа выхода электрона А = 6,3 эВ), при облучении у-квантом с энергией ε=1,53МэВ.

2. Определите длину волны ɣ-излучения, падающего на платиновую пластину (работа выхода электрона из платины А = 6,3 эВ), если максимальная скорость фотоэлектронов была υ_max= 3 Мм / с.

3. Определите максимальную скорость υ_max фотоэлектронов, вырываемых с поверхности меди (работа выхода электрона А = 5,2 эВ), при облучении ɣ-излучением с длиной волны λ= 2,5пм.

4. Определите, на какое максимальное расстояние от поверхности электрода может удалится фотоэлектрон, вырванный с поверхности серебряного электрода при облучении его монохроматическим светом с длиной волны λ = 85 нм, если вне электрода имеется задерживающее электрическое поле напряженностью Е = 10 В / см. Красная граница фотоэффекта для серебра λ₀ =264 нм.

5. Фотоэлектроны вырываются с поверхности серебряной пластинки (работа выхода А = 4,7 эВ) фотонами с энергией ε = 5эВ. Определите максимальный импульс, передаваемый поверхности этой пластинки при вылете электрона и полный импульс, полученный пластинкой.

6. Если освещать катод вакуумного фотоэлемента монохроматическим светом с длиной волны λ₁= 350 нм, то фототок прекращается при задерживающем напряжении U₁=12,5 В. Как изменится задерживающее напряжение при увеличении длины волны на 20%?

7. На поверхность металла падает пучок ультрафиолетового излучения (λ= 0,25 мкм). Красная граница фотоэффекта λ₀ = 0,62 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?

8. При освещении катода вакуумного фотоэлемента мо­нохроматическим светом частотой v₁ = 2∙10¹⁵ Гц фотоэлектроны полностью задерживаются тормозящим полем при напряжении U₁= 7 В. При увеличении частоты падающего света на 45% за­держивающее напряжение оказалось равным U = 10,7 В. Вы­числите по этим экспериментальным данным постоянную План­ка.

9. Энергия фотона равна кинетической энергии электро­на, имевшего начальную скорость υ ₀ = 10 м/с и ускоренного разностью потенциалов U= 4 В. Определите длину волны фото­на.

10. Уединенный цинковый шарик облучают монохромати­ческим светом длиной волны λ = 40 нм. Определите, до какого потенциала зарядится шарик. Работа выхода электронов из цин­ка A = 4,0 эВ.

11. Определить работу выхода А_вых электронов из натрия, если красная граница фотоэффекта λ₀ = 500 нм.

12. Будет ли наблюдаться фотоэффект, если на поверхность серебра направить ультрафиолетовое излучение с длиной волны λ =300нм?

13. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта λ₀ =307 нм и максимальная кинетическая энергия W фотоэлектрона равна 1 эВ?

14. На поверхность лития падает монохроматический свет (λ =310нм).
Чтобы прекратить эмиссию электронов, нужно приложить
задерживающую разность потенциалов U не менее 1,7 В. Определить работу выхода А.

15. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов U ₁=3,7 В. Если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу A выхода электронов с поверхности этой пластинки.

16. На цинковую пластинку падает монохроматический свет с длиной волны λ =220 нм. Определить максимальную скорость υ _maxфотоэлектронов.

17. Определить длину волны λ ультрафиолетового излучения падающего на поверхность некоторого металла, при максимальной скорости фотоэлектронов, равной 10 Мм/с. Работа выхода электронов из металла пренебречь.

18. Максимальная скорость фотоэлектронов υ _max ,вылетающих из
металла при облучении его γ- фотонами, равна 291 Мм.
Определить энергию Eγ -фотонов.

19. Определить максимальную скорость фотоэлектронов, вы­летающих из вольфрамового электрода, освещаемого ультрафи­олетовым светом с длиной волны 0,2 мкм.

20. Катод вакуумного фотоэлемента освещается светом с длиной волны 0,38 мкм. Фототок прекращается при задер­живающей разности потенциалов равной 1,4 В. Найти работу выхода электронов из катода.

21. Цинковый электрод освещается монохроматическим све­том. Фототок прекращается при задерживающей разности потен­циалов 0,4 В. Вычислить длину волны света, применявшегося при освещении.

22. Красной границе фотоэффекта соответствует длина волны 0,332 мкм. Найти длину монохроматической световой волны, падающей на электрод, если фототок прекращается при задер­живающей разности потенциалов, равной 0,4 В.

23. Найти величину задерживающей разности потенциалов для фотоэлектронов, испускаемых при освещении цезиевого элек­трода ультрафиолетовыми лучами с длиной волны 0,3 мкм.

24. На цинковую пластинку падает монохроматический свет с длиной волны λ =220 нм. Определить максимальную скорость v _max фотоэлектронов.

25. Найти постоянную Планка, если фотоэлектроны, вырываемые из поверхности металла светом с частотой 1,2∙10¹⁵ Гц задерживаются разностью потенциалов 3,1 В, а вырываемые светом с длиной волны 125 нм - задерживаются разностью потенциалов 8,1 В.

26. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны 83 нм. Определите на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью 10 В/см. Красная граница фотоэффекта для серебра 264 нм.

27. При освещении металлической пластинки монохроматическим светом задерживающее напряжение равно 1,6 В. Если частоту света увеличить в два раза, то задерживающее напряжение будет 5,1 В. Определить в электрон вольтах работу выхода электрона.

28. Определить скорость фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовыми лучами с длиной волны λ₁=0,155 мкм; 2) ɣ-лучами с длинной волны λ₂=0,01 А. Работа выхода для серебра А=4,7 эВ.

29. Красная граница фотоэффекта для цезия λ₀=6530 А. определить максимальную скорость фотоэлектрона при облучении цезия фиолетовыми лучами с длинной волны λ=4000 А.

30. Источник монохроматического света мощностью P=64 Вт испускает ежесекундно 10²⁰ фотонов, вызывающих фотоэффект на пластинке с работой выхода электронов, равной А=1,6 эВ. До какого потенциала зарядится пластинка при длительном освещении?

 

 

Тема 3. Эффект Комптона

Эффектом Комптона называется изменение длины волны рентгеновского излучения при его рассеянии веществом, содержащим легкие атомы. Эффект открыл А. Комптон в 1923 году. Рассмотрим рассеяние кванта монохроматического рентгеновского излучения на неподвижном электроне (рис. 3.1).

Квант электромагнитной волны с импульсом падает на неподвижный электрон. В результате взаимодействия электрон приобретает импульс .Импульс рассеянного кванта уменьшается до . Угол α - это угол между направлениями падающего и рассеянного кванта.

 

Передвинем импульс вправо и разложим его на составляющие и в соответствии с законом сохранения импульса.

 

Длина волны рентгеновского излучения, рассеянного под углом a, больше длины волны l, падающего на вещество излучения, на величину D l, зависящую только от угла a:

(3.1)

где м - постоянная величина, называемая комптоновской длиной волны электрона. Величина D l представляет собой изменение длины волны рентгеновского излучения. Эффект Комптона не удается объяснить на основе классической волновой теории света, т.к. он является релятивистским квантовым эффектом.

Согласно квантовой теории, эффект Комптона - результат упругого столкновения рентгеновского фотона со свободным или почти свободным электроном. При этом фотон передает электрону часть своей энергии и часть своего импульса в соответствии с законами сохранения энергии и импульса.

Если первоначально электрон находился в покое, то по закону сохранения энергии можно записать

,

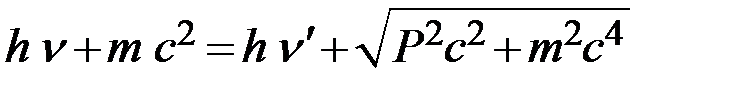здесь - энергия падающего кванта рентгеновской волны, 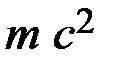- энергия покоя электрона, - энергия рассеянного кванта.

Энергия релятивистского электрона после взаимодействия с квантом равна ; 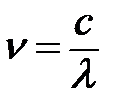и - частоты падающего и рассеянного рентгеновского излучения, т – масса покоя электрона, Р - импульс электрона, называемого после столкновения электроном отдачи.

Запишем закон сохранения импульса, используя рис. 3.2,

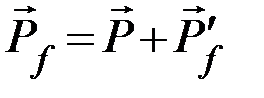или .

Возведем в квадрат

. (3.2)

Импульс фотона можно переписать в виде

, .

Подставляя формулы импульсов фотона в закон сохранения импульса, получаем

.

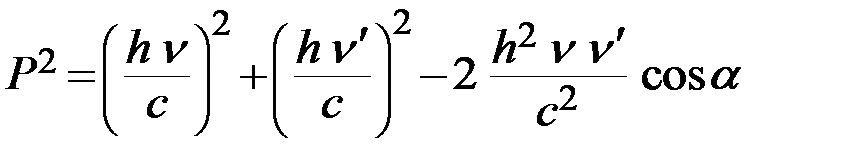Перепишем закон сохранения энергии

.

Возведем в квадрат

.

Найдем квадрат импульса электрона

. (3.3)

Приравняем правые части формул (3.3) и (3.2)

,

.

Подставим формулы частот и и после преобразований получим

.

Сокращая, можем записать

;

.

Обозначим комптоновскую длину волны электрона

, (3.4)

получим формулу изменения длины волны излучения, совпадающую с выражением (3.1)

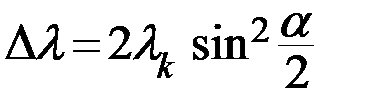. (3.5)

Если рассеяние происходит на протоне, то масса m в формуле (3.4) является массой покоя протона и - комптоновская длина волны протона.

Кинетическая энергия электрона отдачи равна разности энергии падающего на вещество фотона

и энергии рассеянного фотона ,

.

Выражая частоту фотона через длину волны, можно записать

.

Заменим изменение длины волны фотона и , получим

.

Подставим формулу (3.5) изменения длины волны фотона

.

Кинетическая энергия электрона W_k максимальна при рассеянии на угол a = p и равна

.

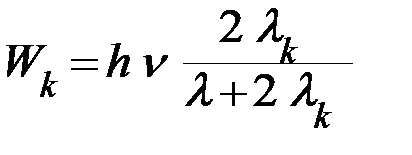ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ

Пример 1. Фотон при комптоновском рассеянии на первоначально покоившемся свободном электроне рассеивается на угол Энергия рассеянного фотона составляет = 0,2 МэВ. Определить изменение длины волны фотона и энергию фотона до рассеяния.

Дано: ; = 0,2 МэВ

Найти: Δλ -? e -?

Запишем формулу изменения длины волны фотона для эффекта Комптона

Решение:

здесь , м -комптоновская длина волны электрона. Подставляя значения, получаем

=2,43·10^-12м.

Для определения энергии фотона применим формулу Планка ε = hν. Частоту фотона выразим через длину волны ν = с/λ, тогда

Ε = hс / λ и λ = hс/ ε.

Подставляя в формулу Комптона, можно записать

.

где энергия покоя электрона равна .

Проведя преобразования, получаем

Энергия покоя электрона равна Е₀ = 0,511 МэВ, тогда

ε = = 0,33 МэВ

Ответ: Δλ = 2,43·10^-12м, e = 0,33 МэВ.

 

Пример 2. Фотон с длиной волны 5 пм рассеивается на первоначально покоившемся свободном электроне под углом α = 60⁰. Определить энергию рассеянного фотона и кинетическую энергию электрона отдачи.

Дано: λ= 5 пм; α = 60⁰

Найти: 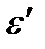-? W_к -?

Решение

 

Запишем формулу Комптона .

Выразив длину волны через энергию фотона λ` = hс / ε`, получим

.

Проводя преобразования выразим :

= 3,88·10^-14(Дж) =3,88·10^-14/(1,6·10^-19) эВ = 0,243 МэВ.

2) Кинетическая энергия электрона отдачи в соответствии с законом сохранения энергии равна разности между энергией e падающего фотона и энергией 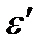рассеянного фотона:

W_к = ε - ε’ = hс/ λ -ε ׳= 0,248-0,243 = 0,005 МэВ

Ответ: 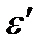= 0,24 МэВ, W_К = 5кэВ.

ЗАДАЧИ

1. Вычислить максимальное изменение длины волны при комптоновском рассеянии рентгеновских квантов на свободном протоне.

2.Определить изменение длины волны рентгеновского излучения при рассеянии под углом 90° на свободных, первоначально покоившихся электронах.

3. Длина волны комптоновского рассеяния фотона на свободном электроне изменяется на 0,036 Å. Найти угол рассеяния фотона.

4. На свободном неподвижном электроне рассеивается фотон с энергией 1 МэВ. Вычислить кинетическую энергию электрона отдачи, если длина волны фотона увеличилась на 25 %.

5. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния 90⁰. Определить энергию и импульс рассеянного фотона.

6. Найти энергию фотона, рассеянного под углом 120⁰ на первоначально покоившемся электроне, если начальная энергия фотона была равна 250 кэВ.

7. Фотон с длиной волны 20 пм испытывает комптоновское рассеяние под углом 120⁰. Найти изменение D l длины волны рентгеновского излучения при рассеянии и кинетическую энергию электрона отдачи.

8. Найти долю энергии фотона, которая передается электрону отдачи при эффекте Комптона. Энергия рентгеновских фотонов до рассеяния равна 10 кэВ, а угол рассеяния 60⁰.

9. Фотон с энергией 0,4 МэВ рассеивается под углом 90⁰ на свободном электроне. Рассчитать энергию рассеянного фотона и кинетическую энергию электрона отдачи.

10. Определить долю энергии, которую фотон передал электрону, при рассеянии фотона с длиной волны 0,01 Å на свободном электроне под углом 120⁰.

11. Вычислить долю энергии фотона, которая приходится на электрон отдачи при комптоновском рассеянии, если рассеяние фотона происходит на угол 180⁰, а энергия фотона до рассеяния равна 0,2 МэВ.

12. Угол рассеяния фотона в эффекте Комптона 90⁰. Угол отдачи электрона 30⁰. Определить энергию падающего фотона.

13. Рентгеновское излучение с длиной волны 10 пм испытывает комптоновское рассеяние на первоначально покоившихся электронах. Определить энергию электрона отдачи и угол рассеяния, если изменение длины волны составило 3 пм.

14. Определить изменение длины волны рентгеновского излучения при рассеянии под углом 60° на свободных, первоначально покоившихся электронах.

15. Определить изменение длины волны рентгеновского излучения при рассеянии под углом 90° на свободных, первоначально покоившихся протонах.

16. Фотон с энергией 0,2 МэВ испытывает комптоновское рассеяние под углом 90° на свободном электроне. Определить энергию электрона отдачи и энергию рассеянного фотона.

17. Фотон с длиной волны 2,4 пм рассеивается на первоначально покоившемся электроне под углом 90°. Определить частоту рассеянного излучения.

18. Определить изменение длины волны рентгеновского излучения при рассеянии под углом 180° на первоначально покоившихся свободных электронах.

19. Рассчитать длину волны рентгеновского излучения, если при комптоновском рассеянии под углом 60° длина волны рассеянного излучения увеличилась до 60 пм.

20. Фотон с энергией 1 МэВ рассеивается на первоначально покоившемся свободном электроне. Определите угол рассеяния фотона, если длина волны рассеянного фотона равна комптоновской длине волны 2,43 пм.

21. Монохроматическое рентгеновское излучение рассеивается на свободных электронах. Длины волн рассеянного излучения под углами 60° и 120° отличаются в 1,5 раза. Определить длину волны падающего рентгеновского излучения.

22. Фотон с длиной волны 5 пм испытывает комптоновское рассеяние под углом 90° на первоначально покоившемся свободном электроне. Определите изменение длины волны при рассеянии и энергию электрона отдачи.

23. Фотон с энергией 0,2 МэВ рассеивается на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20%.

24. Фотон с энергией 0,2 МэВ испытывает комптоновское рассеяние под углом 60° на свободном электроне. Определить энергию электрона отдачи.

25. Фотон с энергией 0,1 МэВ в результате комптоновского эффекта рассеялся при столкновении со свободным электроном на угол 90°. Определить энергию фотона после рассеяния.

26. Определить энергию рассеянного под углом 120° фотона на покоящемся свободном электроне, если первоначальная энергия фотона была равна 250 кэВ.

27. Рассчитать частоту рассеянного фотона и кинетическую энергию электрона отдачи при комптоновском рассеянии фотона с длиной волны 6,0 пм под прямым углом на покоящемся свободном электроне.

28. Кинетическая энергия электрона отдачи равна 0,45 МэВ. Фотон рентгеновского излучения рассеивается под углом 120° на покоящемся свободном электроне. Вычислить энергию фотона до рассеяния.

29. Определить изменение длины волны электромагнитного излучения при рассеянии под углом 180° на первоначально покоившихся свободных протонах.

30. Вычислить максимальное значение изменения длины волны при комптоновском рассеянии фотонов на свободном электроне.

 

Тема 4. Строение атома

В 1911 году в лаборатории Э. Резерфорда при исследовании рассеяния альфа-частиц в веществе было открыто ядро атома.

На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель строения атома. В центре атома находится положительно заряженное ядро, вокруг которого движутся электроны. Размеры атома ~ 10^-10 м, размеры ядра r_я ~ 10^-15 м.

Ядро состоит из протонов и нейтронов. Нейтрон не имеет электрического заряда. Заряд протона равен + е, здесь е - элементарный электрический заряд. В ядре находится N протонов, поэтому заряд ядра равен + Nе, где N - порядковый номер элемента в таблице химических элементов Д.И. Менделеева.

В нейтральном атоме вокруг ядра движутся N электронов.

В 1913 году Н. Бор разработал теорию строения атома водорода и водородоподобных атомов (содержащих один электрон: …).

Основу теории Бора составляют два постулата.

1. Существуют такие стационарные состояния атома, в которых он не излучает энергию. Стационарными являются состояния, для которых момент импульса электрона кратен постоянной Планка,

ħ. (4.1)

Здесь ħ = называется постоянной Планка, как и h; n -главное квантовое число, которое принимает целые значения n = 1, 2, 3,...

2. При переходе из одного стационарного состояния в другое атом излучает или поглощает квант энергии

.

- энергии электрона, находящегося в стационарных состояниях. Рассмотрим теорию строения водородоподобного атома по Бору.

На электрон, движущийся в атоме вокруг ядра, действует электрическая (кулоновская) сила притяжения к ядру (рис. 4.1). Запишем второй закон Ньютона для электрона в атоме

.

Подставим кулоновскую силу притяжения электрона к ядру в атоме

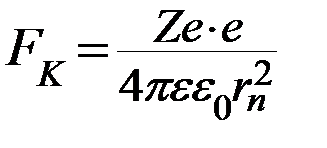
и нормальное ускорение

,

во второй закон Ньютона, получим

.

. (4.2)

 

Из формулы первого постулата Бора (4.1) найдем скорость электрона

, (4.3)

подставим ее в соотношение (4.2) и учтем ε=1

.

Получим радиус орбиты электрона

. (4.4)

 

В атоме водорода один протон Z = 1; для первой орбиты электрона n=1

= 0,53 м (радиус первой боровской орбиты);

=2,1 м, = 4,8 м, …, .

Определим скорость электрона в атоме, подставив в формулу (4.3) радиус орбиты электрона (4.4),

;

.

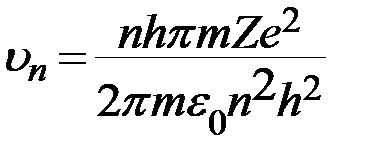В атоме водорода для n = 1 скорость электрона = 2,2 м/с.

Полная энергия электрона в атоме равна сумме кинетической и потенциальной энергии

.

 

Заменяя кинетическую энергию по формуле (4.2), можно записать

;

.

 

Подставим в формулу радиус орбиты, получим энергию электрона в водородоподобном атоме

.

В атоме водорода энергия электрона равна: .

 

Энергия электрона отрицательна, т.к. он находится в атоме в связанном состоянии

= − 13,55 эВ; = − 3,39 эВ;

= − 1,5 эВ, …, .

Определим частоту излучения кванта энергии водородоподобным атомом

; ;

.

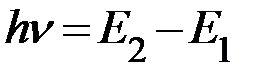Обозначим постоянную Ридберга для водорода

.

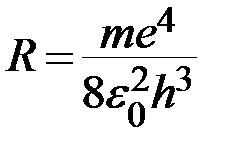после вычислений получим значение .

Для частоты кванта после введения постоянной можно записать

.

Для атома водорода заряд ядра

(4.5)

Формула (4.5) называется обобщенной формулой Бальмера.

Учитывая , получаем обобщенную формулу Бальмера для длины волны

,

где м^-1 также называется постоянной Ридберга, ,

.

Изучение спектров разреженных газов обнаружили, что у каждого газа свой линейчатый спектр, состоящий из отдельных спектральных линий. И. Бальмер подобрал формулу, расчеты, по которой совпадают с экспериментальными значениями длин волн, соответствующих спектральным линиям атома водорода в видимой области спектра

(рис. 4.2)

, n = 3, 4, 5,...

 

Формулу можно записать для част